Адресные волоконные брэгговские структуры в квазираспределённых радиофотонных сенсорных системах

Радиофотоника ‒ современное направление научных исследований, изучающее взаимодействие оптического излучения и радиочастотного сигнала в задачах приёма, передачи и обработки информации.

Общей проблемой опроса множества волоконных брэгговских структур (ВБС) в волоконно-оптических и радиофотонных сенсорных сетях (РФСС) является сложность и дороговизна приборов их опроса, обусловленная применяемыми технологиями мультиплексирования датчиков [1–5]. Волновое [1], временное [2], частотное [3], поляризационное [4] и пространственное [5] мультиплексирование требуют применения таких сложных устройств, как оптические анализаторы спектра, спектрометры с перестраиваемыми интерферометрами Фабри–Перо, с дифракционными решётками, излучение которых принимается и анализируется на ПЗС-матрицах и т.д.

Сложность применяемых технологий мультиплексирования и опроса объясняется и ещё одним важным фактором – опрашиваемые датчики не являются адресными, поэтому любое перекрытие спектров ВБС приводит к существенным ошибкам измерений [6–8]. Несомненно, условная адресация у датчиков есть. Они, как указывалось выше, имеют различные центральные длины волн, объединены пространственно в различные группы, расположены на различных расстояниях от источника зондирования и т.д. Последний фактор широко используется в импульсных системах адресного кодированного опроса, комбинированных с другими видами мультиплексирования [9–11]. Преимущество использования условной адресации нашло применение при построении сенсорных сетей на основе интерфе-

Параллельно с разработкой технологий мультиплексирования и опроса развивались методы создания спектрально-кодированных ВБС, информация о структуре которых позволила бы обеспечить полное разделение откликов от датчиков, работающих в одном и том же диапазоне частот [14–17]. Спектрально-кодированные датчики основаны на технологии кодового мультиплексирования [16–17]. В частности, используются оптические ортогональные коды для формирования спектральной структуры ВБС, уникальной для каждого датчика. Опрос спектрально-кодированных ВБС производится в режиме реального времени с помощью определения функции автокорреляции между отражённым от датчика спектром и его кодовой сигнатурой. В ряде работ продемонстрировано обнаружение и отслеживание датчиков для эффективного измерения температуры и деформации даже в условиях перекрытия при использовании кодов Слепяна на основе ортогональных дискретных протяжённых сфероидальных последовательностей [18–21]. Однако и для их опроса требуется источник двухчастотного сканирующего излучения и электронный векторный анализатор для проведения дополнительных вычислений.

В последнее время в практику радиофотонных сенсорных сетей вошли ВБС со случайной спектральной структурой [22–25]. Когда параметры окружающей среды изменяются, спектральные ком- поненты ВБС со случайной спектральной структурой сдвигаются аналогично сдвигу центральной длины волны обычной ВБС. После корреляции с эталонным спектром отражённый случайный спектр, уникальный для каждой ВБС, может быть значительно сжат, что определяет возможность измерений с высоким разрешением [22]. Однако и для таких измерений необходим оптический спектральный анализатор, что уменьшает скорость опроса в сенсорной системе. Упрощение системы опроса было достигнуто при использовании импульсного зондирования и проекции отражённых случайных спектров на линейно чирпи-рованную ВБС, что позволяет перенести спектральную информацию о сдвиге на шкалу времени и получить дополнительный выигрыш в разрешающей способности измерений [23–25]. При этом для регистрации требуется цифровой процессор определения сверхмалых временных интервалов, определяемых временем прихода импульсных откликов от пространственно разнесённых датчиков.

Более простое решение может быть найдено при использовании адресных волоконных брэгговских структур (АВБС), которые бы могли одновременно и выполнять функции формирователя двух- или поли-гармонических излучений, и продолжать оставаться чувствительным элементом РФСС, если значение разностной частоты будет инвариантно к контролируемым физическим полям, а набор разностных частот будет ортогонален в массиве таких датчиков.

АВБС не отличаются по своей природе и принципами реакции на воздействие физических полей от классических ВБР. Отличие подхода состоит в методике определения их центральных частот. Все остальные задачи построения решаются на основе известных и ранее разработанных принципов, что делает перспективным применение РФСС на АВБС для задач одно-, мало- и многосенсорных приложений.

Адресная волоконная брэгговская структура

Адресной волоконной брэгговской структурой назовём такую структуру в оптическом волокне, которая удовлетворяет следующему набору требований. При направлении на неё широкополосного лазерного излучения с равномерной амплитудно-частотной характеристикой она в оптическом диапазоне формирует двухчастотный сигнал, разность между частотами которого много меньше несущих оптических частот и находится в радиочастотной области спектра. Разностная частота между двумя частотными составляющими инвариантна к воздействию физических полей и не меняется при смещении центральной частоты АВБС. Полная ширина на половине высоты спектральных составляющих, образующих двухчастотный отклик, одинакова и много меньше разностной частоты .

Существует как минимум два теоретических подхода к формированию АВБС с инвариантным расстоянием между её адресными частотами при воздействии на неё измеряемых полей. Первым подходом является использование волоконных брэгговских решёток (ВБР) с двумя симметричными фазовыми п-сдвигами (2п-ВБР), а вторым - использование двух идентичных разнесенных по длине волны сверхузкополосных ВБР (2Х-ВБР).

Волоконные брэгговские решётки с двумя симметричными фазовыми π-сдвигами привлекают внимание разработчиков волоконно-оптических датчиков [26–28], поскольку они достаточно легки в производстве и могут быть изготовлены при помощи фазовой маски с минимально предъявляемыми требованиями к параметрам модуляции коэффициента преломления и равномерности характеристик его профиля [29, 30]. АВБС 2π-ВБР представляет собой три последовательно расположенные ВБР с фазовыми π-сдвигами между ними. Широкополосное лазерное излучение, прошедшее через 2π-ВБР, формирует двухчастотное излучение в области окон прозрачности, соответствующих спектральному расположению двух симметричных фазовых π-сдвигов вблизи центральной частоты средней решётки. АВБС в виде 2λ-ВБР структуры также просты в производстве и могут быть получены с использованием стандартного ультрафиолетового лазера и применения нанометровых подвижек, как показано в [31]. При записи может быть использована как фазовая маска, так и другие интерферометрические схемы. В работах [32, 33] предложен метод записи АВБС с помощью механического натяжения оптического волокна.

Характерной особенностью АВБС как 2λ-ВБР, так и 2π-ВБР является инвариантность расстояния между адресными частотами в амплитудно-частотной плоскости при наложении на них деформационных или температурных полей, что позволяет использовать эту характерную особенность АВБС для формирования адреса при мультиплексировании их в массив датчиков.

Основа метода измерительного преобразования

Чтобы АВБС можно было использовать в качестве чувствительных элементов РФСС, необходимо потребовать выполнения двух дополнительных условий. Первое условие – в область анализа светового потока попадает отклик только от двух формирующих адрес частот каждой АВБС на всем измерительном диапазоне. Второе условие – АВБС, имеющие одинаковую центральную (брэгговскую) частоту, должны иметь различные адресные частоты.

Подход к определению смещения центральной (брэгговской) частоты основан на оптическом преобразовании результирующего сигнала от АВБС в линейном наклонном фильтре с наклонной амплитудночастотной характеристикой и оптоэлектронном преобразовании оптического сигнала в радиочастотный диапазон на фотоприёмнике с последующим решением системы нелинейных уравнений, полученных адресной частотной фильтрацией результирующего сигнала после фотоприёмника.

Форма спектрального отклика АВБС в амплитудночастотной плоскости после прохождения излучения через фильтр с наклонной амплитудно-частотной характеристикой приведена на рис. 1, где использованы обозначения: ω С – центральная (брэгговская) частота АВБС; ω – частота левой частотной составляющей; δ – полная ширина на половине высоты частотных компонент, формирующих адрес; Ω – адресная частота; u и v – параметры линейного наклонного фильтра.

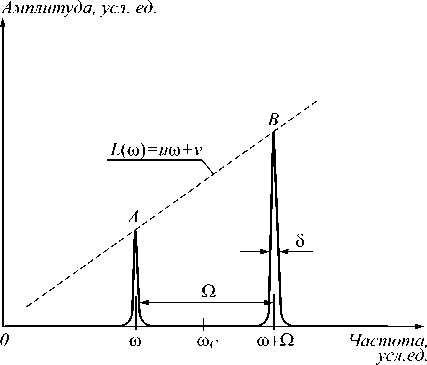
Рис. 1. Форма спектрального отклика АВБС

Оптико-электронная схема опроса одиночной АВБС представлена на рис. 2.

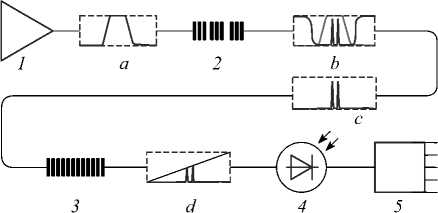
Рис. 2. Оптико-электронная схема опроса АВБС

Лазерный источник 1 с шириной полосы излучения, соответствующей измерительному диапазону, формирует непрерывное лазерное излучение, которое, проходя через АВБС 2, формирует двухчастотное непрерывное лазерное излучение (диаграмма с на рис. 2). Излучение проходит через фильтр 3 с наклонной амплитудно-частотной характеристикой и образует асимметричное двухчастотное лазерное излучение (диаграмма d ), которое поступает на фотоприёмник 4 и принимается на аналого-цифровом преобразователе 5. Микроконтроллер, производящий математическую обработку сигнала, на рисунке не приведён.

Смещение центральной (брэгговской) частоты АВБС ведёт к изменению взаимного отношения амплитуд двухчастотного отклика от АВБС, что влечёт за собой изменение глубины модуляции и амплитуды колебаний двухчастотного биения результирующего отклика от АВБС на фотоприёмнике.

Уравнение огибающей кривой двухчастотного биения результирующего отклика от АВБС на фотопри-

ёмнике зависит от амплитуд левой и правой частотных составляющих и имеет вид:

S ( t , ω C ) = A ² + B ² + 2 AB cos( Ω t +ϕ ),            (1)

где A – амплитуда левой и B – правой частотных составляющих, формирующих адрес, которые зависят от положения центральной (брэгговской) частоты АВБС: A = A ( ω C ) и B = B ( ω C ), φ – разность фаз оптических несущих. Коэффициент модуляции (2) огибающей биений (1) можно использовать как единственный измеряемый параметр для определения центральной (брэгговской) частоты АВБС:

M ( _ω ) ₌ 2 ⋅ A ( ω C ) ⋅ B ( ω C ) .

^C A ²( ω C ) + B ²( ω C )

Зависимость коэффициента модуляции огибающей (2) – монотонная функция, зависящая от смещения центральной (брэгговской) частоты АВБС (рис. 3). Следовательно, существует обратная функция ω C ( M ), позволяющая определить смещение брэгговской частоты АВБС по известному значению коэффициента модуляции.

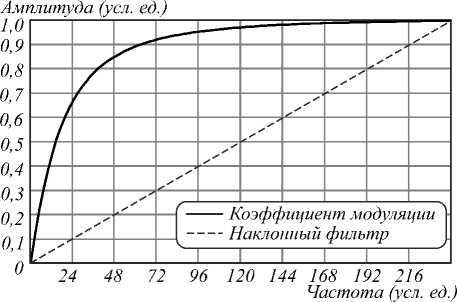
Рис. 3. Зависимость коэффициента модуляции от смещения центральной частоты АВБС: сплошная линия – коэффициент модуляции;

пунктирная – параметры наклонного фильтра

Главным требованием является то, что зависимость коэффициента модуляции от смещения центральной (брэгговской) частоты АВБС должна быть заранее детерминирована при известных параметрах наклонного фильтра для каждой АВБС.

Несмотря на то, что зависимость коэффициента модуляции от смещения центральной часты АВБС – монотонная и позволяет решать задачу определения смещения центральной частоты АВБС под воздействием физических полей, и, как следствие, определения величины этого воздействия, она не обеспечивает равномерности шкалы измерений. Кроме того, необходимо обеспечить и независимость измерительной информации от флуктуаций мощности светового потока на фотоприёмнике, не связанных с воздействием измеряемых физических полей.

Для линеаризации шкалы измерений можно использовать фильтры с нелинейной амплитудно-частотной характеристикой. Например, фильтры с амплитудно-частотной характеристикой, подчиняющей- ся степенному закону, или, например, фильтры с экспоненциальной формой профиля (3):

L ( to ) = e^C '" ) ^П - 1. (3)

где to max — максимальное значение диапазона измерений, а n и C – параметры фильтра.

При применении нелинейных фильтров недостаток неравномерности шкалы измерений нивелируется. Другим вариантом улучшения разрешающей способности шкалы измерений является возможность наложения двух встречных наклонных фильтров в разных плечах отражённого сигнала и проведения измерения в том плече, в котором бóльший уровень сигнала.

Избежать флуктуаций мощности светового потока на фотоприёмнике, не связанных с воздействием физических полей на АВБС-сенсор, предлагается при помощи нормировки мощности светового потока за счёт создания двух каналов – опорного без наклонного фильтра и измерительного с наклонным фильтром, и нормировки величины коэффициента модуляции (2) на полную мощность в опорном канале.

В рамках предложенной оптико-электронной схемы дополнительно необходимо решить задачу температурной стабилизации фильтра с наклонной частотной характеристикой, чтобы избежать искажений сигнала, связанных с его температурным дрейфом. Задача температурной стабилизации фильтра решается стандартным для этого методом и не рассматривается в рамках этой работы.

Математическая модель

Применение двух (и более) АВБС с одинаковой центральной (брэгговской) частотой в измерительной системе обладает рядом преимуществ. Во-первых, это значительно снижает требования к диапазону рабочих частот всех оптических компонент системы. Во-вторых, как следствие, ведет к значительному удешевлению стоимости применяемых компонент. В-третьих, является путем к унификации компонент сенсорной системы. Вместе с этим возникают и дополнительные сложности в определении центральных (брэгговских) частот АВБС в массиве сенсоров, поскольку в системе возникают множественные перекрестные биения всех частотных компонент, формирующих адресные частоты АВБС.

В измерительной системе не накладывается никаких дополнительных ограничений на взаимное расположение массива АВБС во всем диапазоне измерений, следовательно, на фотоприемнике будут происходить все возможные комбинации перекрестных биений всех частотных компонент, формирующих адреса АВБС. Кроме того, в системе могут возникать частоты биений как повторяющиеся, так и кратные адресным частотам АВБС, что существенно усложняет поиск и идентификацию их центральных частот.

Несмотря на это, был найден метод обработки комплексированного сигнала, принятого от массива АВБС с одинаковой центральной частотой и разными разностными частотами, который позволяет решить задачу однозначного определения положений центральных частот всех АВБС в массиве сенсоров.

Функциональная оптико-электронная схема опроса массива АВБС сенсоров приведена на рис. 4, на котором использованы обозначения: 1 – источник лазерного излучения с шириной спектра, соответствующий максимальному диапазону измерений; 2.1–2. N – массив АВБС-сенсоров; 3 – фильтр с наклонной амплитудно-частотной характеристикой; 4 и 7 – измерительный и опорный фотоприемники; 5, 8 – измерительный и опорный АЦП; 6, 9 – делители, 10 – сумматор мощности светового потока.

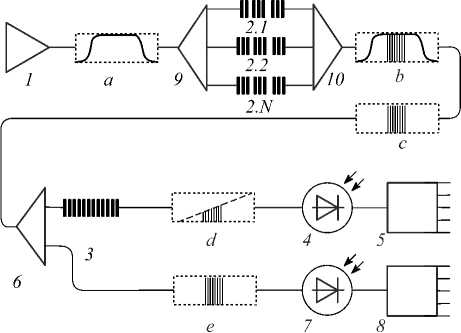
Рис. 4. Функциональная оптико-электронная схема опроса массива АВБС

Буквами a – e на рис. 4 обозначены схемы спектральных характеристик оптического излучения на соответствующем участке оптико-электронной схемы. Форма спектрального отклика сигнала, поступающего на измерительный фотоприемник, приведена на рис. 5, на котором использованы обозначения: to i -положение левых, to i + Q i - положение правых составляющих; to Br - центральная (брэгговская) частота; Q i - адресные частоты АВБС; амплитуды левой и правой гармоник, образующих адресную частоту, обозначены A i и B i . Разностные частоты Q i сенсоров, объединенных в массив, не совпадают.

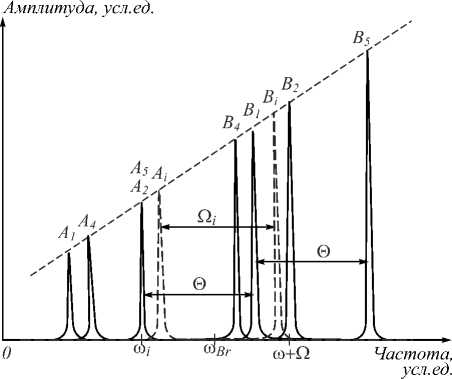
Рис. 5. Форма спектрального отклика сигнала, поступающего на измерительный фотоприемник

На фотоприемнике, как на нелинейном квадратичном элементе, возникают парные биения всех частотных составляющих – Ai и Bi. Полученный сложный сигнал принимается на аналого-цифровой преобразователь и служит источником информации для определения центральных длин волн всех входящих в измерительную систему сенсоров.

Суммарный отклик массива АВБС i на фотоприёмнике равен квадрату суммы откликов всех частотных компонент, входящих в сигнал (4):

F ( t ) =

Z A i sin( to i t ) + B i sin(( to i + Q i ) t )

Запись выходного сигнала в виде (4) позволяет выполнить преобразования, исключающие из записи (4) все оптические высокочастотные слагаемые и перевести анализ сигнала в радиочастотный диапазон. Для чего разобьем выражение (4) на две отдельные суммы, вынесем постоянный множитель за скобки суммирования, возведем выражение в квадрат, изба- вимся от степени в множителе, выполнив процедуру понижения степени, получим промежуточное выражение для полной формы сигнала. Поскольку фотоприемник не чувствителен к колебаниям мощности на оптических частотах, то из промежуточного выражения для полной формы сигнала можно без потери физического смысла исключить все слагаемые с колебаниями на частотах выше, чем максимальная адресная частота АВБС. Результирующий сигнал после фотоприемника на АЦП имеет вид (5):

( A i A k cos(( to i

NN

P ( t ) = zz i = 1 k = 1

AB cos(( to i

B i A _k cos(( to i

_v B i B _k cos(( to i

- ю k ) t ) +

- to k - Q k) t) +

- to k + Qi) t) +

— tok + Qi — Qk) t) ?

Узкополосная фильтрация сигнала (5) на адресных частотах АВБС-сенсоров позволяет получить систему уравнений (6), которая дает возможность определить положение центральных (брэгговских) частот всех АВБС в массиве:

f            (Qj-toi to1|)2

Ai Ake"    2

NN zz i = 1 k = 1

(Qj -|toi-tok-Qk )2 AiBke      252+

( П , -|ш ₍ -ш i +Q j |)²

Bi Ake      252+

= D j , j = 1, N ,

(Q j -h-rn k +Q ₁ -Q k |)²

4 BiBke ~ где Dj - амплитуда сигнала на частоте Qj, множитель с экспонентой при каждом слагаемом описывает частотный фильтр на адресной частоте на частоте Qj.

Система уравнений (6) может быть решена только численно. Наиболее подходящим методом для решения систем уравнений такого класса являются итерационные методы – модифицированный метод Ньюто-на–Рафсона или метод Левенберга–Марквардта, которые обладают квадратичной сходимостью.

Неизвестными величинами в системе уравнений (6) являются to j . Амплитуды A j и B j связаны с to j через известные параметры наклонного фильтра (7):

Aj = L (to j) = u to j + v ,

B j = L ( to j -+Q j ) = u ( to j +Q j ) + v .

Все итерационные методы предполагают задание начальных условий для старта и обеспечения сходимости итерационного процесса. Чтобы обеспечить сходимость метода, в качестве начальных условий можно принять данные, полученные в качестве решения системы уравнений (6) в условиях отсутствия вклада перекрестных биений. В этом случае система уравнений (6) становится совокупностью независимых друг от друга уравнений, каждое из которых может быть решено как квадратное уравнение:

toj = -2- [Vu2Q2+ 4DH — (uQj + 2v)] . (8)

Можно показать [34], что (8) в качестве начальных условий является необходимым и достаточным для сходимости итерационного метода решения системы уравнений (6).

Некоторые результаты численного моделирования

Рассмотрим наиболее часто встречающийся случай произвольного взаимного расположения массива АВБС, когда их взаимное расположение не предполагает неоднозначности в определении их положений. То есть для каждой адресной частоты АВБС получаем отклик только от той АВБС на адресной частоте, на которой происходит опрос. На рис. 6 а показано ситуационное взаимное расположение массива из четырех АВБС, при котором правые и левые частотные составляющие не совпадают, а их взаимное расположение не образует разностных частот, совпадающих с адресными; на рис. 6 б приведена низкочастотная часть спектра результирующего оптического сигнала.

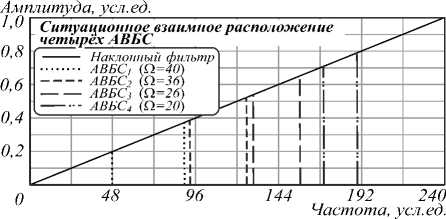
а)

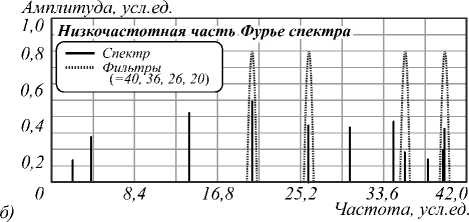
Рис. 6. Ситуационное взаимное расположение четырех АВБС (общий случай)

Решение системы уравнений относительно to j при начальных приближениях, заданных по формулам (8), имеет вид:

' 48,0000 ' 90,0000 130,0000 ^ 164,0065 ,

' 2,2450 - 10 ^{- 5} ^ 3,2323 - 10 - 7 3,9749 - 10 ^{- 7} _ч - 6,5192 - 10 ^{- 3} ,

В (9) s – вектор результатов решения системы уравнений (6), E – вектор абсолютной погрешности вычислений.

Обратим внимание на то, что в качестве начальных значений для реальной измерительной системы можно (и нужно) выбирать те значения положений АВБС, которые были получены на предыдущем расчетном шаге по времени, поскольку скорость измерений гораздо выше скорости изменения измеряемых физических полей.

Как можно видеть из (9), максимальная погрешность нахождения положений центральной частоты АВБС составляет 6,5191^10^–3 усл. ед., что в безразмерных параметрах математической модели соответствует физической частоте ~ 6,5 МГц. Принимая во внимание, что 1 ГГц соответствует 0,008 нм, получим, что максимальная погрешность определения положения АВБС составляет порядка 0,05 пм.

Интересным является ситуационный случай такого взаимного расположения АВБС в массиве, который образует многократные частоты, равные адресным. Результаты расчетов согласно математической модели показывают, что и в этом случае максимальная погрешность определения положения левой частотной составляющей АВБС составляет не более 0,008 усл. ед. (8 МГц), что в 10–50 раз превышает возможности классических методов определения смещения центральной частоты сенсора.

При численном моделировании была проведена оценка влияния ширины частотного фильтра на результаты измерений. Расположив АВБС таким образом, чтобы в частотной области не возникали кратные частоты и чтобы амплитуды левой и правой частотных составляющих АВБС в массиве не совпадали друг с другом, были созданы условия, чтобы в частотный диапазон одного из адресных частотных фильтров попадала близкая, но не равная ей частота.

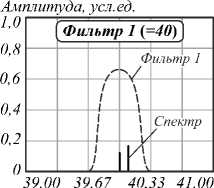
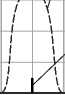
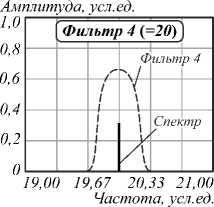
На рис. 7 представлены спектрограммы результата фильтрации электрического сигнала после фотоприемника в случае возникновения в системе частот, экстремально близких к адресным частотам АВБС.

Результаты расчетов для данного случая показывают, что и в этом случае максимальная погрешность определения частоты АВБС составит не более 1 усл. ед. (1 ГГц), что приводит к максимальной погрешности определения центральной длины волны АВБС в 8 пм, что можно считать вполне приемлемой точностью.

Выводы

В результате проведенных исследований разработан и предложен новый класс сенсорных систем – ра- диофотонные сенсорные системы на адресных волоконных брэгговских структурах. Проведенные исследования включали в себя создание концепции, теории и техники адресных волоконных брэгговских структур, разработку принципов построения единого поля волоконно-оптических датчиков и радиофотонную методику обработки измерительной информации. Показано, что применение указанных систем позволяет решить важную научно-техническую проблему – улучшить метрологические и технико-экономические характеристики, а также расширить функциональные возможности существующих радиофотонных сенсорных систем.

Амплитуда, усл.ед.

0.6

0.4

0.2

1,0 0.8

Частота, усл.ед.

Фильтр 2 (=36)

Фильтр 2

Спектр

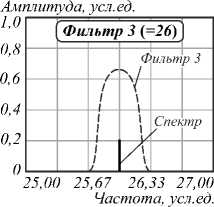
Рис. 7. Результат фильтрации на адресных частотах АВБС при частотах, экстремально близких к адресным

0 35,00 35,67 36,33 37,00 Частота, усл.ед.

На основе созданной математической модели решена задача однозначного определения центральной (брэгговской) частоты каждой из АВБС в условиях возможного возникновения кратных или дублирующих ложных частот. Предложен подход к уменьшению погрешности измерений, основанный на анализе величины мощности сигнала огибающей на выходе фильтра, отнесенного к его полной мощности на выходе адресной структуры.

Проведены численные и натурные эксперименты, показавшие возможность повышения разрешающей способности проводимых измерений при использовании АВБС в 10–50 раз по сравнению со способами, использующими классические решетки. Например, обеспечить максимальные значения погрешности измерения температуры в 0,1 % и давления в 0,5 % от полной шкалы измерения, что, соответственно, в 2 раза лучше при сравнении со сдвоенным датчиком температуры и давления на безадресных решетках. Диапазон изменения температур, в котором проводились измерения, составлял 40– 150 °С, а диапазон изменения давления – 100–600 атм.

Полученные выигрыши в метрологических характеристиках обусловлены разработкой эффективных процедур математической обработки измерительной информации. В частности, разработаны модели и проце- дуры однозначного определения адресных частот каждого датчика в мало- и многосенсорных массивах, исключения ложных адресных частот, динамического наблюдения за положением датчиков во времени, трехчастотной асимметричной по амплитуде калибровки, определения параметров адресной структуры для обеспечения заданной точности и диапазона измерений.

Работа выполнена при финансовой поддержке Минобрнауки Российской Федерации в рамках государственного задания КНИТУ-КАИ №8.6872.2017/8.9.