Акустические и упругие свойства сплава Cu 3Au в интервале температур 300 K

Для физики конденсированного состояния важно знать о нелинейных свойствах веществ. Ангармонические свойства твердых тел связаны с отклонением поведения среды от закона Гука. Это означает, что связь между напряжением и деформацией становится нелинейной. В качестве меры ангармонизма межатомных (межмолекулярных) колебаний и нелинейности сил взаимодействий между атомами служит параметр Грюнайзена. Упругие свойства кристаллов наиболее востребованные свойства всех твердых тел, которые проявляются при их деформировании вследствие внешних воздействий. В качестве характеристик упругих свойств кристаллов служат различные модули и константы упругости, адекватно отражающие природу межатомных сил связей, что является одной из основных задач физики твердого тела. Анизотропия упругих свойств позволяет судить о прочности межатомной связи по различным плоскостям кристалла.

Упругие свойства и ангармонические эффекты изучались нами ранее в металлических, ионных, ковалентных, ионно-ковалентных и молекулярных кубических монокристаллах с разными типами решеток [ 1-3 ] . Представляет интерес изучение анизотропии упругих свойств и ангармонизма межатомных взаимодействий в двойных сплавах с позиционным порядком-беспорядком. Рассмотрим сплав типа А₃В, а именно Cu₃Au. В области низких температур сплав имеет кубическую гранецентрированную решетку с пространственной группой Pm 3 m, в которой атомы меди занимают центры граней, а атомы золота находятся в вершинах куба. Выше Т с =661 К сплав существует как высокотемпературная разупорядоченная форма, имеющая гранецентрированную кубическую решетку, в которой атомы Cu и Au распределены по всем позициям без дальнего порядка. В работе [ 4 ] изучались упругие свойства сплава методом составного пьезоэлектрического вибратора в интервале температур 293…723 К (особенно тщательно в окрестности Т с ).

Расчетные соотношения

На основе данных по c ij ( Т) [ 4 ] кристалла Cu₃Au проведен расчет скоростей распространения чисто продольных и поперечных упругих волн в трех кристаллографических направлениях для фактора упругой анизотропии ( А ), соотношения Коши ( А ), как для упорядоченной, так и для разупорядоченной форм в широком интервале температур. Скорости звука в направлениях [ 100 ] , [ 110 ] и [ 111 ] рассчитывали по формулам:

ρν² L[100] = c 11 , 2ρν² L[110] = c 11 + c 12 + 2c 44 , 3ρν² L[111] = c 11 + 2c 12 + 4c 44 ,

ρν2t[100] = c44, 3ρν2t[111] = c11 + c44 – c12, pv2t[1io] = c44, (волна поляризована в направлении [ oo у]), pv2t2[iio] = c11 — c12 (волна поляризована в направлении г 1 у01).

Постоянные жесткости в измерены с погрешностями: с 11 – 0,8%, с 12 – 1,13%, с 44 – 0,23%. Исходя их этих погрешностей, максимальная погрешность в определении скоростей в любом направлении не превышает 0,5%.

Фактор упругой анизотропии, определяющий меру изотропности кристалла, определяли по соотношению: А=2с44/с11–с12 (для упругоизотропного тела А=1). Соотношение Коши – мера центральности сил межатомного взаимодействия (при А=1 все силы межионного взаимодействия в кристалле должны быть центральными), равно отношению А=с 12/ с44. Упругие свойства изотропных твердых тел характеризуются модулями упругости В (модуль объемной упругости или модуль всестороннего сжатия), Е (модуль Юнга), G (модуль сдвига), для нахождения которых использовали приближение Voigt-Reuss-Hill (VRH) (кубическая сингония):

В = В фрх = В Ф + ^{В р} , В ф = 1 / 3( c „ + 2 c _|2), ^1/B p =3 ( 5 11 + ² 5 12 ) ,

G = G фрх = ^{G ф} 2 G Р , G ф = 1/5 ( c 11 - c 12 + 3 c ₄₄ ) , 1/ G p = 1/5 [ 4 ( 5 _n - 5 12 ) + 3 5 44 ] ,

P _ P _ ^ЕФ ^{+ Е} Р _г _ ⁽ с 11 ^— с 12 ^{+ 3} с 44 ⁾⁽ с 11 ^{+ 2} с 12 )

Е Е фрх i ^, Е Ф ^_                                 ,

• ^{2                          2} с 11 ^{+ 3} с 12 ⁺ с 44

Е _ ⁵ с 44 ⁽ с 11 ^— с 12 ⁾⁽ с 11 ^{+ 2} с 12 )

с 44 ^{( 3} с 11 ⁺ с 12 ) ^{+ (} с 11 ^— с 12 ) ⁽ с 11 ^{+ 2} с 12 )

Постоянные податливости связаны с постоянными жесткости для кубических кристаллов формулами:

, _ c 11 ⁺ c 12 5 _ c 12 5 _ ¹

(c 11 — c 12 )(c 11 + 2c 12 )             (c 11 — c 12 )(c 11 + 2c 12 )

Эти постоянные использовались для расчета модулей упругости сплава Cu3Au в разных кристаллографиче- ских направлениях по следующим соотношениям:

• —-— ^{_ 5} 11 , 7     ^{_ 5} 44 , "y = 7 ⁵ 11 ^{+ 5} 12 ^{+ 0,5 5} 44 ), —-— ^{_ 5} 11 ^{— 5} 12 ⁺ 0,5 ⁵ 44 ,

E 100         G 100         E110    2

—    ^{_ 5} 11 ^{— 2} / ^{3( 5} 11 ^{— 5} 12 ^— 0, ^{5 5} 44 ), —---- = ⁵ 44 ⁺ 4 / ^{3( 5} 11 ^{— 5} 12 ^{— 0,5 5} 44 ).

E111

Формулы для расчета коэффициента Пуассона по трем особым направлениям σ приведены в табл. 1.

Традиционный подход в оценке ангармонизма межатомных колебаний в твердых телах связан с определе- ниемтермодинамического параметра Грюнайзена у[5]:    PBSв

^Y "  с , р '

где в - температурный коэффициент объемного расширения, BS - динамический (адиабатический) модуль объемной упругости (модуль всестороннего сжатия), ц - молярная масса, СР - молярная теплоемкость при посто янном давлении, р - плотность вещества.

Расчетные формулы по коэффициентам Пуассона кубических монокристаллов

Таблица 1

Параметры	Направление в кристалле (направление деформации)
	< 100 > (001)	< 110,001 >	< 110,1 10 >	< 111 > (111)
s ij	s 12 — 5 1Г	2 5 12	— 5 11 + 5 12 — 0,5 5 44 5 11 + 5 12 + 0,5 5 44	5 11 + 2 5 12 — 0,5 5 44
		5 11 + 5 12 + 0,5 5 44		5 11 + 2 5 12 + 5 44
c ij	c 12	2 c 12	3 BC ’ — c 11 c 44	3 B — 2 c 44
	c 11 + c 12	c 11 + 3 B C 7 c 44	3 BC ’ + c 11 c 44	6 B + 2 c 44

Примечание:        1             ,       1

C 2 ⁽ c 11 c 12 )              3^ 11          12

В качестве меры ангармонизма межатомных колебаний в работе [6] предложен вариант с позиций физиче ской акустики:     3 [ 3^42^^^,^ | Здесь UL и ut - скорость распространения продольных и поперечных упру-

^Y 2 ( и^г 2 + 2 u _t ² J '

гих волн в пространственно неограниченной среде.

Результаты и их обсуждение

Температурные изменения рассматриваемых в работе характеристик сплава Cu3Au в интервале 300…725 К представлены в табл. 2 и на рис. 1-4. Они линейны как в упорядоченной, так и в разупорядоченной фазах, за исключением узкого температурного диапазона вблизи Тс«661 К. При этом постоянные жесткости, скорости звука и модули упругости слабо уменьшаются с ростом температуры, а коэффициенты Пуассона и составляющие параметра Грюнайзена демонстрируют тенденцию роста. В табл. 2 приведены результаты вычислений температурных изменений скоростей чисто продольных и поперечных упругих волн в трех кристаллографических направлениях, фактора упругой анизотропии и соотношения Коши.

Из рис. 1 видно, что все три усредненных упругих модуля ( Е , G , B ) сплава Cu 3 Au вблизи Т с испытывают аномальное поведение («смягчение», уменьшаются в виде «ступеньки» порядка 10%), связанное, естественно, с переходом в разупорядоченное состояние его критической решетки.

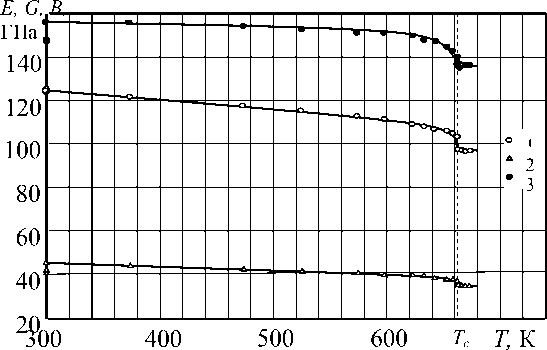
Рис. 1. Температурная зависимость упругих модулей поликристалла Cu3Au:

1 – модуль Юнга Е , 2 – модуль сдвига G , 3 – модуль всестороннего сжатия В

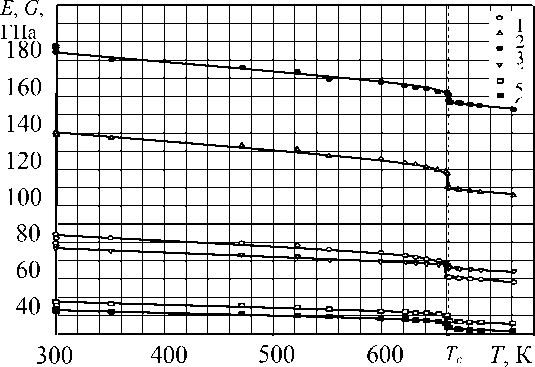
Рис. 2. Температурная зависимость упругих модулей монокристалла Cu3Au в разных кристаллографических направлениях: 1) E<100>; 2) E<110>; 3) E<111>; 4) G<100>; 5) G<110>; 6) E<111>

Анизотропия упругих свойств сплава Cu3Au сказывается на соотношении между модулями Юнга и сдвига в разных кристаллографических направлениях (рис. 2). Неравенства между модулями упругости данного сплава аналогичны известным зависимостям между Е и G для галогенидов лития при А>1: Е<111>>Е<110>>Е<110> и G<100>>G<110>>G<111>. Температурные изменения коэффициентов Пуассона в сплаве Cu3Au в разных кристаллографических направлениях приведены на рис. 3, здесь же приведены изменения с температурой коэффициента Пуассона для поликристалла. В температурном диапазоне от 300 до 725 К выполняется следующее соотношение: σ<110, 001> > σ<1001> > σ<1111> > σ<110, 1ī0> . В окрестности Тс коэффициенты Пуассона при деформации кристалла Cu3Au в двух направлениях (< 100 > и < 1 10 Л 1 0 > ) скачком возрастают (примерно на 10%). Скорости звука были использованы далее для определения температурных изменений составляющих параметра Грюнайзена по кристаллографическим направлениям ч^н; сплава Cu3Au (рис. 4). В соответствии с установленной нами ранее закономерностью для Yhky кубических кристаллов при стандартных условиях в зависимости от фактора упругой анизотропии [7] ориентационные параметры Грюнайзена сплава Cu3Au сохраняют неравенство между собой во всем исследованном интервале температур: Y2[iio]>Y[iii]]>Yi[iio]]>Y[ioo] при А>1. Ангармонизм колебаний атомов решетки высокотемпературной разупорядоченной фазы сплава Cu3Au возрастает в направлении [iii] и [ii0] при поляризации поперечной волны в направлении [ i To ] и уменьшается в направлении [i00] и [ii0] при по ляризации поперечной волны в направлении [ o o Г] .

Увеличение ангармонизма при переходе порядок-беспорядок происходит резко (скачком). Уменьшение ангармонизма при переходе порядок-беспорядок происходит плавно (непрерывно). Максимальное изменение параметра Грюнайзена при переходе порядок-беспорядок составляет 15, минимальное – 7%. Указанные особенности ангармонизма межатомного взаимодействия вблизи Т с свидетельствуют о том, что переход в Cu 3 Au является частично изотермическим (переходом 1-го рода), а частично плавным (переходом 2-го рода).

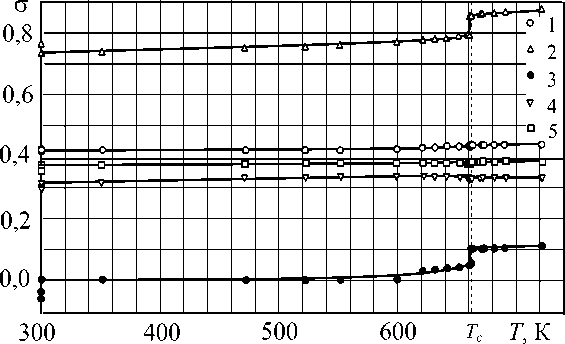
Рис. 3. Температурная зависимость коэффициентов Пуассона монокристалла Cu3Au в разных кристаллографических направлениях:

1) <100>; 2) <110, 001>; 3) 110,1 10 ; 4) <111>; 5) для поликристалла

Таблица 2

Скорости упругих волн ( и , м/с), фактор упругой анизотропии и соотношение Коши сплава Cu 3 Au в диапазоне 300…723 К из данных s ij ( Т ) [4]

Т , К	[ ioo ]		[ iio ]		[ iii ]		А	A
	U l	U t	U l	U t 2	U l	U t
300	3952	2330	4348	1465	4472	1800	2,532	2,086
373	3947	2305	4336	1446	4458	1779	2,541	2,144
473	3922	2273	4306	1418	4426	1750	2,569	2,199
523	3903	2257	4284	1403	4404	1735	2,586	2,218
573	3881	2232	4258	1383	4378	1714	2,605	2,255
598	3875	2219	4249	1366	4367	1698	2,637	2,290
623	3815	2206	4228	1348	4347	1683	2,677	2,302
633	3827	2200	4206	1339	4325	1676	2,699	2,285
643	3815	2193	4195	1328	4314	1667	2,665	2,291
653	3783	2187	4165	1317	4287	1659	2,756	2,265
658	3758	2182	4144	1307	4265	1651	2,788	2,247
661	3721	2175	4109	1299	4231	1644	2,802	2,213
661	3652	2157	4062	1218	4190	1594	3,143	2,229
663	3638	2155	4050	1215	4178	1591	3,141	2,213
668	3650	2152	4060	1212	4188	1588	3,154	2,243
673	3641	2149	4052	1208	4180	1585	3,162	2,241
683	3641	2143	4050	1202	4178	1580	3,177	2,257
693	3638	2138	4047	1196	4174	1574	3,193	2,270
723	3608	2122	4016	1181	4136	1559	3,227	2,270

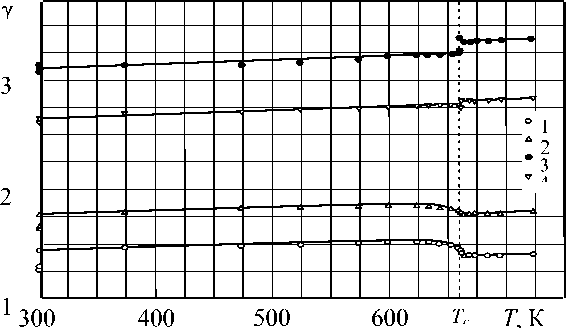
Рис. 4. Составляющие параметра Грюнайзена сплава Cu₃Au: 1) Y [ i _O o j ; 2) Y i eh o j ; 3) У 2 [ ₁₁₀ ] ; 4) У [ 1И ]

Заключение

На основе сведений по постоянным жесткости монокристаллического сплава Cu 3 Au проведен расчет скоростей звука по трем особым направлениям. При этом установлено, что среди скоростей распространения продольных волн максимальное значение имеет u _L [ ₁₁₁ ] , а скорость поперечных волн максимальна в направлении [ 100 ] во всем интервале температур. Температурные зависимости упругих модулей (Юнга, сдвига, всестороннего сжатия) линейны (модули уменьшаются с ростом температуры, за исключением окрестности температур вблизи Т с ). Температурные изменения коэффициентов Пуассона также линейны, однако а с ростом температуры незначительно увеличивается. Аналогично коэффициенту Пуассона изменяются и составляющие параметра Грюнайзена (слабый рост γ с увеличением температуры).