Акустические, упругие и ангармонические свойства твердых растворов с промежуточной валентностью Sm 1-xTm xS

В последней четверти прошлого века большой интерес исследователей вызвал новый класс полупроводников – редкоземельные полупроводники [1]. Почти одновременно с этими системами с нецелочисленной валентностью, например, иона самария, начал формироваться и в настоящее время интенсивно развивается еще один новый класс материалов, получивший наименование ауксетики [2]. Ауксетики обладают необычными механическими свойствами, обязанными, в первую очередь, отрицательному коэффициенту Пуассона. Примечательным фактом является то обстоятельство, что в некоторых составах твердых растворов SmS с моносульфидами редкоземельных элементов состояния с промежуточной валентностью одновременно характеризуются и отрицательными коэффициентами Пуассона. Наиболее выражена эта взаимосвязь при изоструктурных электронных фазовых переходах, когда проявляется аномально высокая сжимаемость [3]. Рост сжимаемости при фазовых переходах аналогичен уменьшению объемного модуля В. При этом возможны случаи, когда В становится меньше 2/3 G (G модуль сдвига) – материал превращается в ауксетик.

Ранее нами были изучены акустические, упругие и ангармонические свойства соединений с промежуточной валентностью на примере смешанных кристаллов системы Sm х La 1-х S [4] и Sm 1-x Y x S [5, 6]. В данной работе анализируются аналогичные свойства монокристаллов твердых растворов Sm 1-x Tm x S при стандартных условиях (атмосферное давление, Т=300 К).

Исходные экспериментальные данные и расчетные соотношения

Полученные в работе [7] для кубических кристаллов Sm 1-x Tm x S экспериментальные значения постоянной решетки (а), плотности ( р ), постоянных жёсткости (сц, с₁₂, с₄₄), модуля объёмной упругости (В) приведены в табл. 1. Здесь же помещены определённые нами на основе с ij фактор упругой анизотропии А и соотношение Коши А . Из данных таблицы видно, что начальная примесь тулия в системе SmS–TmS резко увеличивает анизотропию упругости и уже составы с концентрацией Tm менее 10 ат.% проходят точку упругой изотропии, при этом А становится >1. Однако уже 15 ат.% тулия вновь повышает анизотропию упругости (А < 0,5). Это говорит о том, что допированием и комбинацией примеси можно сравнительно просто управлять фактором упругой анизотропии данных смешанных систем.

Соотношение Коши ∆ в данных твердых растворах, также как и фактор упругой анизотропии А, во-первых, имеет большие отклонения от единицы (∆=1 – критерий центральности сил межионного взаимодействия), а, во-вторых, принимает даже отрицательные значения для некоторых составов. Физическая сущность последнего факта не совсем понятна. В имеющейся литературе данное обстоятельство никак не объясняется и пока можно только констатировать, что отрицательное значение соотношения Коши присуще аксиально-ауксетичным кристаллам.

Таблица 1 Параметр решетки, плотность, постоянные жесткости, модуль объемной упругости, фактор упругой анизотропии и соотношение Коши кубических монокристаллов Sm 1-x Tm x S при стандартных условиях [7]

	a, Å	р , 103кг/м3	с 11	с 12	с 44	В	А	А
			ГПа
SmS	5,97	5,690	127	12	26,9	50,3	0,468	0,446
Sm 0,90 Tm 0,10 S	5,905	5,946	93	52	23	66	1,122	2,261
Sm 0,85 Tm 0,15 S	5,860	6,114	106	-3	26	33	0,477	-0,115
Sm 0,75 Tm 0,25 S	5,682	6,772	92	-29	37	12	0,612	-0,784

Постоянные жесткости c 11 , с 12 и с 44 кубических кристаллов твердых растворов использовались для расчета постоянных податливости s 11 , s 12 , s 44 , концентрационной зависимости упругих модулей (модуля Юнга E , модуля сдвига G ) и коэффициента Пуассона σ в разных кристаллографических направлениях. Кроме этого, были определены упругие характеристики изотропных твердых растворов (модули упругости В, Е, G, коэффициент Пуассона σ), для нахождения которых использовали приближения Фохт-Ройс-Хилла (ФРХ) [8], Пересада [9] и Александрова [10].

Постоянные податливости связаны с постоянными жесткости кубических кристаллов следующими формулами:

S_t =______ c 11 + c 12 ______ s =         c 12                _s = J_

⁽c 11 - c 12 )(c 11 ^{+ 2c} 12 )             ⁽ c 11 - c 12⁾⁽ c 11 + 2c l2 )               ^c44                     (1)

Модули упругости в разных кристаллографических направлениях определялись по соотношени-

E      s11

ям:     E(100)

-— = s

,

G (100)

F (110)

,

= 2 ^(S11 ^{+ S}12 ^{+ 0,5 S}44 )

,

G (1 10)

= s„ - s₁₂ + 0,5 S 44 )

,

-¹- = S 11 ^{- 2/3(}S 11 ^— S 12 ^{+ 0},⁵S 44 )

E (111)

,

—---= ^s44 ^{- 4/3(s}11 ^{- s}12 + 0,5 ^S44⁾

G (111)                                         (2)

Формулы для расчета коэффициента Пуассона σ приведены в табл. 2. Приближение Фохт-Ройс-Хилла (кубическая сингония)

_ Вф ⁺ B p ^вфрх 2

,

В ф = 1/3(сц + 2с 12 )

,

1/В Р = 3(s 11 + 2s₁₂)

,

г = Gф + Gp

2           G ф = 1/5(0 11

,

1/G p = 1/5[4(s_n — S 12 ) + 3S 44 ]

,

^{— с}12 ^{+ 3с}44 )

,

p Еф + ЕР ефрх     2

Еф =

,

^(с_п   с ,2 ^{+ 3} с 44^)(с_п + ^2с₁2⁾

^2с11 + ^3с12 + ^с44

E p =

,

^5с44^(с11 ^{— с}12^)(с11 ^{+ 2с}12 )

с 44 ^(3с11 ⁺ с 12 ) ^{+ (с}11 с 12^)(с11 ^{+ 2с}12 )

.

Приближения Пересада и Александрова (кубическая сингония)

G = G фРХ + G per + G a

G + 1/8(9В_ф + 4C)GL

G pr = 174^(0 ,, -c i

,,

— 3/8(В ф + 4С ' )с 4 ₄G_Aл — 3/4В ф С ' 0 44 = 0, ₍₄₎

где С ’ = Ч (с ,, - с ,2 ).

Скорости распространения продольных в изотропной неограниченной среде v _L и поперечных v _t упругих волн находили из модулей объемной упругости В и сдвига G по известным соотношениям теории упругости и физической акустики [8]:

V l ² p = B + 4/3G,

v t ² p = G,

где р - плотность вещества. Среднюю ^и и среднеквадратичную ^и к^в скорости звука вычисляли по определению

и3 =■

1/ U + 2/ u 3

,

ч в

ч' +2 u2

.

Среднюю скорость звука использовали для расчета характеристической температуры Дебая 0 D как функции концентрации примесей в исследуемых твердых растворах, а среднеквадратичную скорость для определения их усредненного модуля объемного сжатия [8]:

1/3

_ h ( 3sNp ) _

⁰ D = k 1 4ПМ J ^u       k =ри кв

,,

где h – постоянная Планка, k – постоянная Больцмана, N – число Авогадро, М – молярная масса, s – число атомов в молекуле .

Параметр Грюназейна γ, меру ангармонизма межатомных колебаний и нелинейности сил межатомного взаимодействия, вычисляли через скорости звука [11]:

_Y= 3 (3x² — 4)

^Y 2 (x² + 2)

—

,

Ul

x = —- и t

.

Коэффициент Пуассона квазиизотропных поликристаллов твердых растворов Sm 1-х Tm х S находили по стандартной формуле

3В — 2G

G =-------

2(3В + G)

Результаты и их обсуждение

Согласно теории упругости кубических кристаллов модуль объемной упругости в разных приближениях должен быть одинаковым и В моно- и поликристаллов равны. Расчеты этого модуля для твердых растворов Sm 1-х Tm х S не нарушили данное теоретическое положение (значения В в табл. 1).

Расчетные формулы по коэффициентам Пуассона кубических монокристаллов

Таблица 2

Параметры	направление в кристалле (направление деформации)
	<100> (001)	<110,001>	<110, 110 >	<111> (111)
s ij	s12 — S T	2s 12	S11 + S12 — 0,5s 44	S 11 + 2S 12 — 0,5S 44
		S 11 + S 12 + 0,5S 44
			S 11 + S 12 + 0,5S 44	S 11 + 2S 12 + S 44

c ij	c 12	2c12	3BC ' - C ,, C 44	3B — 2 c 44
		c„ + 3BC ' / c 44
	c ii + ci2		3BC ' + C ,, C 44	6B + 2 c 44

Таблица 3

Модули сдвига поликристаллов твердых растворов Sm 1-х Tm х S по разным приближениям (ГПа)

	G Ф	G Р	G ФРХ	G Пер	G Ал	G
SmS	39,1	34,2	36,7	36,5	36,4	36,5
Sm 0,90 Tm 0,10 S	22,0	21,9	22,0	22,0	22,0	22,0
Sm 0,85 Tm 0,15 S	37,4	32,9	35,1	35,0	35,0	35,0
Sm 0,75 Tm 0,25 S	46,4	43,8	45,1	45,0	44,8	45,0

Модуль сдвига, наоборот, может различаться по величине, что и подтверждают данные табл. 3. При этом все модули сдвига в модели усреднения Фохта, как и следует из теории, оказались больше соответствующих модулей сдвига в модели Ройса (G ф > G Р ). G ФРХ , G Per и G Ал по нашим расчетам достаточно близки (максимальное отклонение между ними не превышает 4%) и для исследуемых составов твердых растворов выполняется неравенство G ФРХ > G Per > G Ал .

Концентрационные зависимости упругих модулей и коэффициента Пуассона в разных кристаллографических направлениях Sm 1-х Tm х S представлены на рис. 1-2. На рис. 2 приведены также зависимости упругих модулей для поликристаллических смешанных систем. В твердых растворах Sm 1-х Tm х S упругие модули и коэффициенты Пуассона в зависимости от их составов изменяются без скачков, разрывов (плавно), но существенно нерегулярным образом. Функции Е (x) монокристаллов твердых растворов Sm 1-х Tm х S (рис. 1а) достаточно сложные. Они содержат совпадающую по значениям модулей Юнга точку при х тулия вблизи 0,1 (первую точку упругой изотропии), затем проходят через максимум (х ≈ 0,15) и опять сближаются (указывают на возможную вторую точку упругой изотропии при х > 0,25).

Для всех составов справедливы следующие соотношения: Е (100) > E (110) > E (111) и G (111) > G (110) > G (100) . Такие неравенства анизотропных упругих модулей характерны для кристаллов с решеткой типа NaCl. Обращают на себя внимание отрицательные значения коэффициента Пуассона в разных кристаллографических направлениях в исследуемых смешанных системах. Это возможно в случае, если материал при продольном растяжении расширяется в поперечном направлении. Подобные аномальные деформационные свойства характерны для нового класса материалов – “ауксетиков”, имеющих большие перспективы для практического применения [2]. При увеличении концентрации ионов Tm³⁺ в сульфиде самария первыми приобретают отрицательные значения коэффициенты Пуассона в кристаллографических направлениях < 100 > и < 110 > (при деформации в плоскости куба), затем о <ш, iii > и последним о <ш, ц₀ > . Собственно ауксетиком ( о <  0) изученная система становится при концентрации примеси сульфида тулия х >  0,2i5.

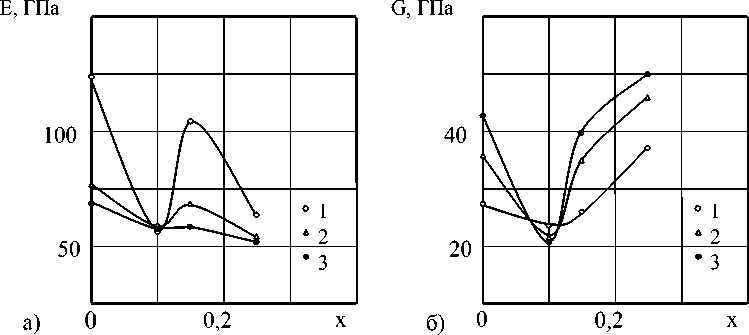
Рис. i. Анизотропия модулей Юнга и сдвига в Sm _i-x Tm x S (а: i - E [ _i00 ] , 2 -Ерю ] , 3 — Ерп ] , б: i — G [ i00 ] , ^{2 -} G [ ii0 ] , ^{3 -} GPU ] )

Таблица 4

Скорости распространения продольных и поперечных упругих волн, средней и среднеквадратичной скоростей звука, температура Дебая, параметр Грюнайзена и коэффициент Пуассона поликристаллов твердых растворов Sm 1-х Tm х S

	υ L	υ t	υ	υ кв	Θ D	γ	σ
		103 м/с			К
SmS	4,171	2,533	2,798	3,174	319	1,316	0,208
Sm 0,90 Tm 0,10 S	3,998	1,924	2,162	2,792	246	2,126	0,349
Sm 0,85 Tm 0,15 S	3,617	2,393	2,618	2,859	302	0,999	0,111
Sm 0,75 Tm 0,25 S	3,245	2,578	2,739	2,818	318	0,315	-0,356

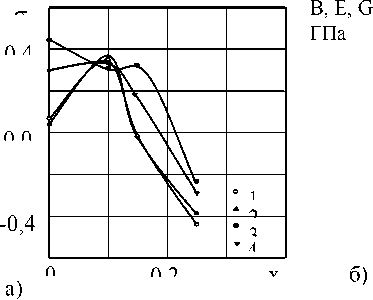
Рис. 2. Концентрационная зависимость коэффициента Пуассона в разных кристаллографических направлениях

			°1 д2
			•3

0,2

х

Модули объемной упругости, Юнга и сдвига для поликристаллов твердых растворов Sm 1-х Tm х S в зависимости от их составов изменяются неодинаково и нерегулярным образом. Повышенная концентрационная зависимость упругих модулей в данном твердом растворе сохраняется для всех составов. В табл. 4 приведены результаты расчетов скоростей звука и остальных параметров по формулам (5)– (9). Они показывают, что для твердого раствора, который можно квалифицировать как ауксетики (σ < 0), отношение скоростей звука ν L / ν t существенно отличается от величины √ 3, то есть здесь явно имеет место нецентральный характер взаимодействия между ионами. Для всех рассматриваемых со-

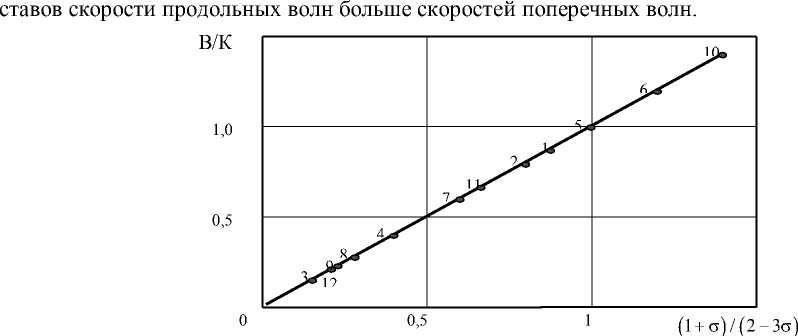
Рис. 3. Зависимость отношения (В/К) от функции коэффициента Пуассона (1+ σ )/(2-3 σ ) для твердых растворов моносульфидов самария, иттрия, их твердых растворов и твердых растворов с примесями лантана и тулия: 1 – SmS, 2 – Sm 0,91 Y 0,09 S, 3 – Sm 0,75 Y 0,25 S, 4 – Sm 0,58 Y 0,42 S, 5 – Sm 0,2 Y 0,8 S, 6 – YS, 7 – Sm 0,90 La 0,10 S, 8 – Sm 0,75 La 0,25 S, 9 – Sm 0_,65 La 0_,35 S, 10 – Sm 0_,90 Tm 0_,10 S, 11 – Sm 0_,85 Tm 0_,15 S, 12 – Sm 0_,75 Tm 0_,25 S

Представляет интерес отдельно остановиться на анализе зависимости – В/К как функции (1+σ)/(2-3σ) для разных составов твердых растворов на основе сульфида самария. Вид указанной функции представлен на рис. 3. Зависимость В/К = f(o) является линейной и проходит через начало координат с наклоном, равном единице.

Заключение

Исследованы анизотропные и изотропные акустические (скорости звука), упругие (модули упругости, коэффициенты Пуассона) и ангармонические (параметры Грюнайзена) свойства монокристаллов твердых растворов Sm 1-х Tm х S при стандартных условиях. Установлено, что все упругие характеристики в области валентного перехода изменяются плавно (сам переход размыт). Обнаружено, что изотропный коэффициент Пуассона принимает отрицательные значения в Sm_1-хTm_хS при х >  0,215. Эти составы твердого раствора представляют собой аксиально-ауксетичные системы. В составах с отрицательными значениями о параметр Грюнайзена принимает минимальные значения, что свидетельствует о гармонизации межатомных (межмолекулярных) взаимодействий в таких кристаллических решетках.