Акустика пористо-упругих насыщенных жидкостью сред (обзор теории Био)

История механики насыщенных жидкостью пористых сред насчитывает уже более полутора сотен лет, отсчитывая свое появление с открытия экспериментального закона фильтрации жидкости в пористой среде — закона А. Дарси (Darcy H.) в 1856 г. [1]. Далее большой вклад в эту проблематику внесли P. Fillunger [2] и K. Terzaghi [3], которые считаются основоположниками первых теорий пористых сред. Отцом современной механики пористых сред является М. Био (Biot M.A.), который в своих многочисленных работах (см. [4] с обзором основных публикаций Био на данную тематику), обобщая работы Terzaghi на случай трехмерных задач, развил в 40–80-х гг. XX в. теорию пористых сред, насыщенных вязкой жидкостью, практически до ее современного состояния. Согласно введению в [4], теория Био является в ХХ в. одним из крупных вкладов в развитие механики сплошных сред, состоящим в обобщении классической теории упругости на область пористых, насыщенных жидкостью сред.

Как сказано в подробном библиографическом обзоре по рассматриваемой тематике [5], "в своих исследованиях Био развил принцип соответствия, согласно которому уравнения, описывающие механику пористых сред, будут формально такими же, как и для упругих или вязкоупругих систем, при условии, что упругие коэффициенты заменены соответствующими операторами".

Далее будем ссылаться лишь на основные работы Био, посвященные распространению колебаний и волн в пористых средах [6–10] (отметим, что имеется перевод на русский язык работ [8–10] — это соответственно работы [11–13]).

Важным разделом механики пористых сред являются задачи акустики пористых насыщенных жидкостью сред, связанные с распространением в них акустических волн. Впервые задачу, связанную с акустикой пористых сред, рассмотрел Я.И. Френкель [14]. В своих первых работах [6, 7] по акустике пористых сред Био описал общую теорию пористых сред, где предполагалось, что среда однородна и изотропна. В дальнейшем эта теория была развита на случаи анизотропного упругого [8] и вязкоупругого скелета [10].

После Био описываемая тематика была развита в многочисленных публикациях, в том числе и в монографиях [15–17], в которых, в частности, содержатся ссылки на библиографические обзоры, посвященные обсуждаемой проблеме.

В теоретических и прикладных задачах научного приборостроения часто приходится иметь дело как с обычными задачами механики пористых насыщенных жидкостью сред (например, случай зонного электрофореза, когда пористая среда (гель) насыщена буферной жидкостью), так и с задачами акустики пористых сред, когда процессы измерений происходят в зернистой среде в условиях наложения звукового поля. Это обстоятельство делает крайне актуальным учет закономерностей теории пористых насыщенных сред в соответствующих задачах теории и практики научного приборостроения.

Наконец, следует отметить, что теория пористых сред не различает случаи собственно пористых сред, когда среда представляет собой единый упругий пористый скелет, насыщенный жидкостью, и зернистых сред, когда в жидкости взвешены отдельные не связанные между собой упругие зерна или частицы (см., например, [6]). Объясняется это особенностями построения математических моделей пористых сред, годных для макроскопического описания существующих в них полей. Макроскопические поля получаются из микроскопических полей (т. е. привязанных к конкретной точке пространства) осреднением последних по некоторому репрезентативному элементарному объему (REV, representative elementary volume). После чего макроскопические поля в пористых средах могут быть описаны в рамках теории сплошных сред. Далее приводятся соображения, исходя из которых выбираются размеры REV. Техника осреднения при переходе от микроскопических к макроскопическим полям приведена, например, в [18].

ЦЕЛЬ ПРЕДПРИНЯТОГО ОБЗОРА ТЕОРИИ

Как правило, в оригинальных работах, монографиях и обзорах по механике пористых сред уравнения макроскопического движения представляются в виде связанной системы уравнений в пространственно-временнóй области. В настоящем обзоре предпочтение будет отдано обзору теории акустики пористых сред в пространственно-частотной области. При этом уравнения движения будут воспроизведены в терминах различных искомых полей. Будут освещены вопросы, связанные с корректной постановкой краевых задач механики пористых сред. Элементы теории стационарных во времени процессов (т. е. не связанных с акустикой) в пористых средах можно прочесть, например, в работах [18, 19].

ИСХОДНЫЕ ДОПУЩЕНИЯ

Теория Био основана на следующих исходных допущениях и предположениях [16, с. 220].

• 1.    Амплитуда смещений, деформаций и скоростей частиц мала, уравнения движения линейны и формализмы в описании полей Эйлера и Лагранжа в первом порядке совпадают.

• 2.    Вследствие макроскопического подхода к рассмотрению соответствующих полей к ним могут быть применены методы механики сплошных сред.

• 3.    Длина волны звуковых колебаний λ должна удовлетворять следующему неравенству:

• 4.    Температурное поле принимается стационарным.

• 5.    Жидкая фаза непрерывна; скелет (матрица) состоит из твердой фазы и незаполненных жидкой фазой пор, которые не учитываются при определении пористости среды.

• 6.    В большинстве случаев материал скелета является изотропным. Анизотропия возникает в случае принудительного вытягивания пор (или трещин).

d ^ l ^ X , где d — средний размер пор (зерен); l — линей- ный размер REV, по которому производится усреднение соответствующих величин.

Таким образом, векторы смещений и тензоры деформации скелета и жидкости являются макроскопически усредненными и корректно определенными в репрезентативном элементарном объеме REV.

Далее величины, относящиеся к скелету, помечаются верхним индексом s , а к жидкой фазе — f . Тогда вектора смещения будут иметь обозначения u ^s и u ^f .

ПРЕДСТАВЛЕНИЕ "u ^s — u ^f "

Вначале изложим версию теории Био [6, 7], представленную в [17, гл. 6] для случая изотропной пористой среды. Неизвестными связанными полями выступают смещения u ^s и u ^f .

Тензоры напряжений, зависящие от смещений, sf для скелета σij и жидкости σij представляются в следующем виде:

0 =[( P - 2 N )9s + Q^ ]5y + 2 NSj,        (1)

О =-Фр5у =(Q^ + R^ )5y,             (2)

где P , Q , R и N — константы; φ — пористость среды, равная отношению объема сообщающихся между собой пор V_f к общему объему V

Vf

Ф = —;

V

0s(f) = V • u   ; p — давление в жидкости; 5 j — единичный тензор (дельта-символ Кронекера).

Константы равны [17, с. 114]:

N = G = ц ;

s

• (1 - ф )I 1 - фb- I K + фK-K, I K^s I

P =-----^^-----------+ - N,

• 1 - ф - K_b IK + ф К / Kf 3

( 1 - ф - K b I K ) Ф К

Q = 1 - ф - Kb IК + Ф К I K

R =

φ ² K^s

1 - ф - K b I K + ф К I K f ^.

Здесь K_b — модуль объемной упругости (bulk modulus) пористой среды в целом при дренажных условиях, т. е. когда поддерживается постоянное давление в поровой жидкости; K^s — модуль объемной упругости упругого скелета; K ^f — модуль объемной упругости жидкости; G — модуль сдвига, совпадающий со вторым параметром Ламе µ теории упругости.

Уравнения движения в пористой среде, насыщенной жидкостью, представляют собой систему двух связанных уравнений. Выпишем ее представление в частотной области в терминах смещений пористой среды [17, с. 120]:

• - го ² ( p _nu s + p_n u f ) =

= ( P - N ) VV- u s + N A u s + Q VV- u ^f ,       (3)

- го ² ( p ₁₂ u s + p ₂₂ u ^f ) = Q VV - u s + R VV - u ^f ,     (4)

где

2 G ⁽ to ) P 11 = P 1 ⁺ P a - ⁱ ^^Ф ^^, ω

2 G ^{( to} )

P 12 = - P a ⁺ '^        ,

ω

2 G ( го ) P 22 = M ⁺ P a ^- i^ -^^.

ω

Здесь приняты следующие обозначения [17]: ρ ₀ — плотность жидкости; ρ ₁ — плотность скелета; ρ _a — эффективная плотность жидкости

P a = M ^X<

( a „ - 1 ) при to ^ 0, ( a ^f ( го ) - 1 ) при го >  0;

af (го) — частотная зависимость извилистости, которая, согласно [17, с. 119], равна

О' ( го ) = a „ + ^V^- G ( го ) ;

i ω q ₀

a „ = lim a _f ( го ) — предельная низкочастотная из- го ^ 0

вилистость. Согласно [15, с. 163], извилистость a„ > 1 (называемая также структурным фактором)

определяется выражением

(1 1 a„ = 1 - rl 1 - l ф где r — параметр, равный 1 / 2 для каркаса, состоящего из сфер, и лежащий в интервале 0 < r < 1 для различных эллипсоидов. Для однородных цилиндрических пор с осями, параллельными направлению градиента давления, a„ = 1, в то время как при случайной ориентации пор a„ = 3. Параметр σ — сопротивление потоку (flow resistivity, см. в [17] выражения и значения для различного характера пористости); ν — отношение Пуассона (см. Приложение); G (го) — весовой частотнозависимый множитель [17, с. 90]

G ( го ) =

₂        1/2

1 + f 2aq0) i® l фЛ J v

Л — характерный размер, заменяющий понятие гидравлического радиуса для общего вида пористости, определяется выражением [17, с. 80]

1/2

Л ₌ 1 8 n^a „ I 1 l °"ф J c

η — динамическая вязкость жидкости; c — константа, близкая к единице; q ₀ — предельная низкочастотная проницаемость при го ^ 0 (частотную зависимость проницаемости q ( ω ) см. в [17, с. 74]).

ТРИ ВОЛНЫ БИО В ПОРИСТОЙ СРЕДЕ

После стандартного представления полей через скалярные и векторные потенциалы us =Vф5 +Vxуs,       uf =Vф-f +Vxуf можно разделить движение в пористой среде на продольные волны (волны сжатия) и поперечные волны (сдвиговые волны). В результате система (3), (4) распадается на две — соответственно для скалярных и векторных потенциалов [17, с. 120–122]:

-го2 (р)цф + Р>12фf ) = PАф + QАфf ,(5)

-го2 (p»12^ + р»22фf ) = QАф + RАфf,(6)

-го2 (.P11Ys + /512Vf ) = NAys,(7)

-го2 (p12Vs + p22Vf ) = 0.(8)

Система (5), (6) в матричном виде записывается так:

-ю2 [M]-1 [р][ф] = А[ф], где

ω ²

Ашs + — N

^р '' Р 22

V     ^р 22

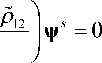
с квадратом волнового числа δ ₃ ² сдвиговой волны

[ M ] =

P

Q

Q

^[ р ^]_

ρ ₁₁

ρ ₁₂

'

;

^P22 _

[ф] =

ϕ ^s ϕ ^f

д 2 _ ^{Ю    Р}''^Р22  ^Р'2

³ N V     ^Р22

Как видно, элементы матрицы [ M ] 'и [ р ] , а следовательно, и элементы квадратной 2 х 2 матрицы ю ² [ M ] ' [ р ] являются постоянными, в общем случае комплексными числами. Следовательно, собственные числа и векторы этой матрицы также являются постоянными. Пусть собственные значения матрицы ю ² [ M ] ' [ р ] равны соответственно δ ₁ ² и δ ₂ ² . Тогда система (5), (6) диагонализируется и записывается в виде [17, с. 121]

"^ [ф'] = A^i ], -g2 [ф2 ] = А [ф2 ] .

В результате получены решения для двух волн сжатия:

^[ ф ' ^]

ϕ 1 ^s

ϕ 1 ^f

^{Ф ]}

ϕ ₂ ^s ϕ 2 ^f

где квадраты волновых чисел δ ₁ ² , δ ₂ ² волн сжатия и константа D равны

• ⁵-    = *» ,, [ P’ + RP" — ² QP"- — ⁵⁵ ] ■

• ²    ( PR ^- Q )

g =            [ Г; ’+Ri5'' -2 QP'2+D5 ],

• ²    ( PR - Q )

5 = [ Pp 22 + Rp^ - 2 Qi 5 '2 ] ² -

• - 4 ( PR - Q ² )( ~_P"p 22 -ft) .

Там же [17, с. 121] получены отношения ф{ / ф ; , i = ',2, амплитуд волн в жидкости и скелете для обеих волн сжатия.

Отметим, что формализм изложения волн сжатия в [17] отличается от оригинального [6] и от изложения в обзоре [5]. Впервые на наличие двух волн сжатия было обращено внимание в работе [14].

Далее получено выражение для единственной сдвиговой волны в скелете

ПРЕДСТАВЛЕНИЕ "u ^s — w"

При изложении этой тематики ориентируемся на работы Био [9, 10], обзор [5] и конспективно написанный раздел "Appendix 6.A :The Biot second representation" из работы [17, с. 131]. Принимаются следующие обозначения: w — смещение жидкости относительно скелета [9, 10]

w _ ф ( u f - u ^s ) ,

^ _ -V • w = -фУ • (uf -us) = ф(в$ -yf),

У =V^ us, yf =V^ uf.

Уравнения состояния в работах Био [9, 10] принимаются в следующем виде:

Gj_ 2^£j+ 5j (ХсУ - aMZ),

pf=-аМУ + MZ .

Здесь σ _ij — суммарный тензор напряжения, приложенный к пористо-упругой среде в целом; ε _ij — тензор деформации скелета. Константы будут выписаны позже.

Запишем уравнения движения, полученные в [9] для случая однородной изотропной среды в терминах u ^s , w :

^Aus + (ц + Xc) VV • us - аМV^ = ^^^ (рus + рfw),

аМVV • us - MV^ = pf —us + Y—w. at2         dt

Или с учетом равенства ^ _ -V • w переписываем последнюю систему

цAu s + (ц + Xc )VV • u s + aM VV • w =

^_ d ^d t 2^{(p u} s ^{+ p f w} ) ,

aM VV • us + MVV • w = рf   us + Y—w.

d t ²          d t

Здесь Y — введенный Био в [9] вязкодинамический оператор, являющийся функцией оператора дифференцирования во временнóй области d t и круговой частоты ω — в частотной; p = (1 - ф) p + фрf — масса единицы объема пористого пространства (см. [6, выражение (3.8)]).

Пользуясь работами [6–10], достаточно неоднозначными в обозначениях, а также обзором [5] с корректными обозначениями, выпишем выражения для введенных в последней системе уравнений постоянных λ _c , α , M :

( K )             к,

M = —’—; а = 1 b- ; X = H - 2 ц ,

Ks       c

ПРЕДСТАВЛЕНИЕ ДЭЗЕЛЯ (DAZEL REPRESENTATION)

В этой модели [20] рассматривается упрощенный случай, когда материал матрицы является несжимаемым. Метод кратко изложен в [17, с. 131, 132]

СМЕШАННОЕ ПРЕДСТАВЛЕНИЕ "u ^s — p "

В этом случае вместо " u ^s —u ^f " -представления используется " u ^s — p " -представление связанной системы уравнений движения. Метод кратко изложен в [17, с. 132–134]. Предполагается однородность порового пространства.

Система (3), (4) с учетом (1), (2) переписывается в виде где

d = K 1 + m

^{s K}

I K

-

;

н=4^+ d - Kb

to ² p 1 1 u s + to ² />₁₂ u f + V • ^ s = 0, to ² p ) ₂₂ u f + to ² p _X2 u ^s - ф V p = 0.

^{+ K}b

⁺ 3 ^ц ;

m = p f а f (в работе [9] указано, что

f извилистость   αf   варьирует в пределах

Использование второго уравнения в (9) позволяет исключить u ^f из этой системы:

a f е [ 1, да ) ); а — коэффициент эффективных на-

пряжений.

Переходя в последней системе уравнений движения в частотную область и полагая все функции гармоническими с фактором e ^{i ω t} , получаем систему (где все величины представлены амплитудами колебаний):

u f =      V^ p - ^p 12- u s .            (10)

ρ ₂₂ ω       ρ ₂₂

Первое уравнение из (9) с учетом (10) переписывается в виде

to ² p u s + ф^P ^ V p + V- ^ = 0,       (11)

^p 22

цАus +(ц + Xc )VV • us + aMVV • w = = -to2 (pus + pfw), aMVV • иs + MVV • w = -to2 pf иs + i toY (to) w.

Выражения вязкодинамического оператора Y в низкочастотной и высокочастотной областях приведены в [9]. Так, в низкочастотной области где p) = (511 - J2^--эффективная плотность.

1 ^ 22

Для исключения имеющейся в ^ ( u ^s , u f ) из (1) зависимости от смещения u ^f из системы (1)— (2) получена эксклюзивная зависимость σ ^s только от смещения u ^s :

Y ( to ) = — + m to . q ₀

* . ( u ' ) = 6 j ( u ' ) - ^ Q p S , .         (12)

В высокочастотной области функция Y ( to ) выглядит так:

η

Y ( to ) =--+ m to .

q ₀

Здесь η — зависимость динамической вязкости от частоты [9]: n = n • F

I to ^

^e— I , to = n / ( q о p f ) ^—

V ^to c I

Здесь σ ˆ _i ^s _j — тензор напряжений скелета в вакууме

<6 ^j = S I K — N l ^ ^s + 2 N s s ;

j У I b 3 I                 j ’ тильда у Q и j? подразумевает, что величины Q, R могут зависеть от частоты и затухания.

После ряда дальнейших преобразований получена следующая система связанных уравнений [17, с. 134]:

некоторая критическая частота.

V-Г5 (u5) + pto2u5 + f vp — 0, nn

A p + — to ² p + 22 Y yto ^V - u ' = 0.

R

Здесь Y определяется выражением

Y — Ф

nx p12

l P

sf

Поля σij и σij определяются соответственно выражениями (1), (2).

КРАЕВЫЕ УСЛОВИЯ В ЗАДАЧАХ АКУСТИКИ ПОРИСТЫХ СРЕД

Постановка краевых условий при решении различных задач акустики пористых сред достаточно полно отражена в обзоре [5, с. 56–58].

ВЫВОДЫ

Таким образом, в обзоре приведены различные связанные уравнения в частотно-пространственной области, позволяющие в том числе и численно решать различные задачи акустики пористых сред.

ПРИЛОЖЕНИЕ

Связь между тензорами напряжения и деформации через удельную потенциальную энергию деформации

Пусть u — ( u1, u2, u3) — вектор смещений в упругой среде. При малых деформациях тензор де-1                     .—      — ..        1 du, d uj формации равен [22, с. 294] £ = — —L + —- , j 2idx,    ax, г ji i, j — 1,3. Как видно, тензор деформации симметричен еу — £ji. Следуя [16], вводим обозначения:

образованного осями i и j (ось x соответствует индексу 1, ось y — 2 и ось z — 3). Вводятся еще две величины, а именно

0 — £ 1 + £22 + £22 , характеризующая относительное изменение объема, и

5 — Г 11 + Г 22 + Г 22 .

Последние две величины являются инвариантами и не зависят от выбора осей координат.

Потенциальная энергия деформации V в единице объема упругой среды в наиболее общем виде определяется так [16]:

2V = Ц a^j .

I J >  I

Здесь a_IJ — коэффициенты, выражаемые через упругие постоянные среды. Если среда изотропная, то последнее выражение преобразуется к такому виду:

2V = c ii ^{( e} _H + e 22 + e зз ) +

^{+ 2 (} c 11 - ² c 66 ⁾⁽ e 11 e 22 ⁺ e 11 e 33 ⁺ e 22 e 33 ^{) +}

⁺ c 66 ⁽ e 12 ⁺ e 13 ⁺ e 23 )

либо к такому:

Г 4 3

2V = i X + 2 ц --ц\02 + 2pd2, где c11 = X + 2ц и c66 = ц ; X и ц — константы Ламе; 0 = V - u; d2 — девиатор d — ei i + e22

2 1 2     2     2 θ

⁺ e 33 ⁺ 2 ⁽ e 12 ⁺ e 13 ⁺ e 23 )    3 .

Величина V связывает тензоры деформации ε _ij и напряжения σ _ij следующим соотношением [16, с. 4]:

e = eu ei — eij

d u,

— ^{— е} “ , d x i

I — 1,2,3;

au  a u"

—+ dx,   ax.

ji

— 2 £ ij , I — 4,5,6, i * j .

Величины £. — £ , £? — £ и £ — £ характе-11 x 22 y 33 z ризуют относительные удлинения линейных элементов в направлении осей, величины 2εij при i * j характеризуют изменение прямого угла,

d V

Г, — —.

ij ^d e ij

Вычисление тензора напряжения в однородной изотропной среде дает следующий результат [17, с. 5]:

rij — X05j + 2ц ,

и окончательно уравнение движения записывается в виде [16, с. 4]:

p ^f u = v- г + F , d t ²

где F — объемная сила (сила, приведенная к единице объема). В терминах вектора смещения уравнение движения имеет вид [17, с. 119; 23, с. 125]:

d ² u

p -—-- = (X + p )VV • u + pAu + F .

С постоянными Ламе λ и µ связаны другие известные упругие постоянные: модуль Юнга E , модуль сдвига G и отношение Пуассона ν :

E _ p(3X + 2p)     _ XX + p ’       2 (X + p) ,

E

G _ P _ ----г.

• 2 ( 1 + v )