Акустооптический затвор для стеклопакетов

Несмотря на многообразие уже существующих устройств на жидких кристаллах (ЖК), учеными всего мира продолжается поиск в решении научных теоретических и экспериментальных задач, инженерных проектов по разработке систем отображения инфор- мации нового поколения, а также оптических приборов. Применение жидких кристаллов привлекательно в этом смысле из-за малости габаритов устройств, малой потребляемой мощности, простоты конструкции, дешевизны, легкой управляемости жидкими кристаллами различными внешними полями (механическим, электрическим, магнитным, термическим).

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

Жидкие кристаллы используют в качестве матрицы для допирования различными нанодобавками [1, 2], используя эффект «гость–хозяин», которые изменяют физические и химические свойства рабочего вещества. Идет поиск вариантов по качеству поверхности электродов и их обработке для создания светофильтров, регуляторов интенсивности света, светоориентируемых линз [3], изучается одновременное влияние, например, электрического и магнитного полей [4]. В работе [5] рассматривалось формирование молекулярного кристалла в объеме НЖК в окрестности p-n перехода, двойным лучепреломлением которого можно управлять электрическим полем. Исследователи находятся в поиске новых пьезоэлектрических материалов и эффектов для создания датчиков, преобразователей, частотных регуляторов [6]. В статье [7] теоретически исследуются условия образования пространственно-модули-рованных фаз вследствие воздействия флексопары в конденсированных средах и жидких кристаллах. Компьютерное моделирование показало общие особенности ферроиков и жидких кристаллов. В обоих веществах формируются пространственно-модули-рованные структуры. Схожие свойства дадут более широкие возможности с точки зрения практического использования этих веществ. В работах [8, 9] изучался прямой флексоэлектрический эффект в окрестности фазового перехода из нематической фазы в изотропную, а также параметры, влияющие на характер флексоэлектрической поляризации. В [10] авторы исследовали ориентационную неустойчивость директора жидкого кристалла в плоской флексоэлектрической ячейке в постоянном электрическом поле, приложенном перпендикулярно к поверхности ячейки. Обнаружено, что при квадратичном воздействии электрического поля ориентационная неустойчивость является пороговой, но беспороговой при линейном воздействии. Используя упругие свойства ЖК и внося в его объем добавки, исследовали связь флексоэлектричества и механотрансдукции [11]. Жидкие кристаллы используются при поиске решения ряда прикладных и фундаментальных задач [12–37], что обосновано экономической и технологической составляющими.

Таким образом, анализ научных работ последних лет показывает интерес к вопросу исследования явлений и эффектов, связанных с флексоэлектриче-ством в жидких кристаллах и в сходных по свойствам материалах. Под действием механического сдвига слой жидкого кристалла деформируется, вследствие чего возникает поверхностная поляризация. В данной работе представлены результаты экспериментального исследования влияния электрического поля на эту поверхностную поляризацию. Статья посвящена не только вопросу изучения флексоэлек-тричества в конденсированных средах, но и предлагается использовать флексоэлектрических эффект для создания акустооптического затвора на жидких кристаллах для стеклопакетов, когда при одной ориентации молекул жидкого кристалла световой поток проходит через ячейку, а при другой нет. Также полученные результаты актуальны для внедрения и разработки устройств памяти, в наноэлектронике и ЖК-мониторах нового поколения.

МАТЕРИАЛЫ И МЕТОДЫ

Материалы

Использовались жидкие кристаллы с гомеотроп-ной ориентацией директора: n – метоксибензилиден – n-бутиланилин (МББА) с ε _α < 0; 4 – октил – 4-цианобифенил (ОЦБ) с ε _α > 0; нитрофенилокти-локсибензоат (НФООБ) с ε _α >0; цианофениловый эфир гептилбензойной кислоты (ЦФЭГБК) с ε _α >> 0, которые находились в нематической фазе. Основные параметры жидких кристаллов представлены в табл. 1.

Таблица 1

Основные физические параметры жидких кристаллов

Жидкий кристалл	Температура мезофазы, оC	е 11, 10–4 ед. СГСЕ/ см	е 33, 10–5 ед. СГСЕ/ см	Дипольный момент, p , D	Диэлектрическая анизотропия, εα
цианофениловый эфир гептилбензойной кислоты (ЦФЭГБК)	К 45 о N 56 о I	5,5	3	~4,5	~19
нитрофенилоктилоксибензоат (НФООБ)	К 45 о А 61о N 68 о I	5,0	1,0	~4,1	>0
n-метоксибензилиден-n-бутиланилин (МББА)	К 18 о N 42 о I	4,5	102	~2,6	~–0,56
4 – октил – 4-цианобифенил ОЦБ	К 22,5о С 34 о N 4 1,3 о I	6,0	1,0	~5,0	~9

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

Методы

Ячейка представляла собой плоский конденсатор, она собиралась из двух пластин, между которыми помещался исследуемый ЖК. Одна из пластин была тонкой, она соединялась с источником колебаний при помощи волновода длиной около 10 см и толщиной 0,5 мм. Частотный диапазон колебаний – от 20 Гц до 20 кГц. В нашем случае частота воздействия была 1 кГц. Толщину ЖК можно было изменять с помощью микрометрического винта (толщина слоев h от 10 до 100 мкм). Ячейка помещалась в термостат для поддержания необходимой температуры, которая контролировалась термопарой [35].

Для экспериментального исследования влияния электрического поля на поляризацию, индуцированную акустическим воздействием, была собрана экспериментальная установка (рис. 1).

Основным элементом ее регистрирующей части является усилительный тракт, состоящий из зарядочувствительного усилителя с большим входным сопротивлением 10 ГОм и селективным усилителем (2 МОм). Зарядочувствительный усилитель в исследуемом диапазоне частот имел коэффициент усиления 2·10², а также относительно малый уровень шумов порядка 50 мкВ. В нем предусмотрена возможность подачи на образец поляризующего напряжения смещения U _c в пределах от 0 до 2·10³ В. Селективный усилитель позволяет регистрировать электрические сигналы в диапазоне 20–10⁵ Гц, нижний уровень которых составляет 4·10^–2 мкВ, а верхний 1 В. Конструкция усилителя позволяет подавать на его вход

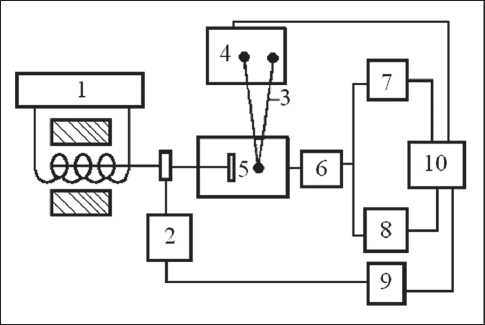
Рис. 1. Блок–схема экспериментальной установки: 1 – звуковой генератор; 2 – селективный вольтметр; 3 – дифференциальная термопара; 4 – микровольтметр постоянного тока; 5 – термостат с ЖК-ячейкой; 6 – предварительный зарядочувствительный усилитель; 7 и 8 – селективные усилители; 9 – измеритель разности фаз; 10 – аналоговый преобразователь постоянное напряжение до 100 В, а также линейное и синхронное детектирование сигналов, которые далее поступают на АЦП, осуществляющий их запись. В случае необходимости одновременного анализа и исследования спектрального состава изучаемого сигнала используются два тракта, каждый из которых независимо друг от друга позволяет обрабатывать спектральные гармоники.

Перейдем теперь к анализу процесса измерения электрических сигналов по вышеописанной методике. Так как исследуемые анизотропные молекулярные жидкости – жидкие кристаллы – являются слабыми электролитами (несовершенными диэлектриками) и обладают достаточно высокой примесной проводимостью σ, то она будет существенно влиять на процесс измерения величины сигналов, индуцируемых ориентационными возмущениями.

Рассмотрим диэлектрик со средней диэлектрической проницаемостью <ε> и проводимостью σ. Допустим, что вследствие каких-либо причин в его объеме возник заряд плотностью σ, который скомпенсирован собственным механизмом проводимости за характерное время τ = <ε> ε _o σ ^{– 1} [34]. В случае ЖК процесс компенсации и переноса заряда определяется физико-химическим механизмом диссоциации и рекомбинации ионов примесной проводимости. В слабых электрических полях, когда время прохода ионов между электродами:

τ = 2η(µ ₊ + µ_)^–1 E ^–1, (1)

(где h – толщина слоя ЖК; µ ₊ и µ _– – подвижности носителей заряда; E – напряженность поля) значительно больше времени рекомбинации, вольт-амперная характеристика жидкого кристалла является линейной от поля, поэтому говорят о константе электропроводности σ.

Если в результате ориентационного возмущения слоя ЖК генерируется поляризация P , то для заряда Q = ʃ P dS , индуцируемого на обкладках конденсатора, эквивалентного ячейке с емкостью, можно записать релаксационное уравнение:

dQ / d τ = ℰ / R – Q / C , (2)

где ℰ – возникающая ЭДС; R – омическое сопротивление ЖК; τ = <ε> ε _o σ^–1 – время релаксации.

Положим, что <ε> = ℰ (ω) ℰ ^{i ω t} и Q = Q _ω ℰ ^{i ω t} , тогда для Q _ω получим решение:

Q _ω = τ/( P ℰ _ω (1+ω² τ²)^–1), (3)

где ℰ _ω – величина ЭДС, определяемая механизмом поляризации и зависящая от частоты возмущения.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

Таким образом, в действительности будет измеряться величина:

ℰ ’ = ωτ ℰ (τ)/(1+ω² τ²). (4)

Из последнего выражения следует, что при малых частотах ω << τ-1 измеряемая ЭДС определяется как ℰ ’ = ωτ ℰ (τ), что отражает процесс маскировки поляризации ЖК ионами проводимости. ω ≥ τ^–1 ЭДС определяется так ℰ ’ ~ ℰ /ωτ, это соответствует диэлектрическим потерям, возрастающим с увеличением частоты возбуждения.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Будем рассматривать поведение индуцированных на поверхности жидкого кристалла зарядов за счет внутренних механизмов молекулярно-ориентационной поляризации в зависимости от величины и направления внешнего электрического поля E . Для этого поместим слой ЖК (ε _α < 0) с начальной гомеотропной ориентацией, например, МББА в электрическое поле. В этой ситуации, когда директор n и электрическое поле E колинеарны, как известно [34], происходит ряд структурно-фазовых превращений типа эффекта Фредерикса, электроги-дродинамической неустойчивости (ЭГДН). Следует ожидать, что ориентационные переходы и непосредственно электрическое поле будет влиять на величину и поведение регистрируемых гармоник U _1ω и U _2ω , по крайней мере, по двум причинам: во-первых, при изменении ориентации (появление наклона директора к поверхности) возникает вклад в общую поляризацию bend-деформации (флексокоэффициент e ₃₃ ), который имеет несколько большее значение, чем e ₁₁ [36]; во-вторых, электрическое поле поляризует среду. Действительно, при увеличении поляризующего напряжения U _c на обкладках ячейки, представляющей конденсатор, происходит сначала увеличение величин сигналов гармоник U _1ω и U _2ω , а затем они после достижения минимума выходят на линейный участок зависимости от поля, который обусловлен конденсаторным эффектом. Необходимо учесть этот вклад в зависимостях, он появляется вследствие изменения толщины слоя ЖК при периодических колебаниях одной из поверхностей ячейки. Его можно измерить экспериментально, переводя мезофазу в изотропное состояние. При этом данная величина будет зависеть от амплитуды колебания пластины a и усредненной диэлектрической проницаемости <ε> = (ε_‖ + 2ε_┴)/3 и слабо отличаться от аналогичной величины в мезофазе.

Проанализируем зависимости гармоник U _1ω и U _2ω от поля (рис. 2). Отметим сразу, что их значения чувствительны к направлению электрического поля,

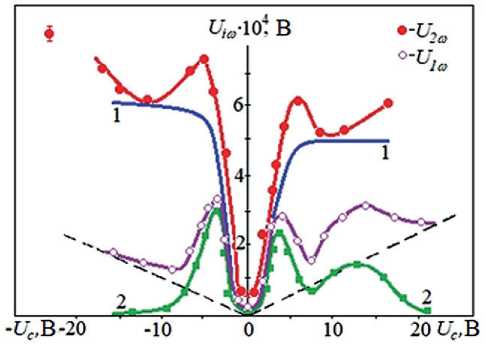
Рис. 2. Зависимости величин первой U _1ω и второй U _2ω гармоник от напряжения смещения U_с : 1 – U _2ω без вклада конденсаторного эффекта; 2 – U _1ω (пунктирная прямая – вклад конденсаторного эффекта; МББА ε _α <0 a = 0,2 мкм; h = 15 мкм; ω = 1 кГц)

то есть при приложении положительного потенциала к деформируемой пластине гармоники достигают меньших значений, чем при отрицательном.

Это связано с двумя причинами. С одной стороны, электрическое поле при положительном потенциале стабилизирует молекулы поляризованного слоя (они в МББА направлены отрицательным концом к поверхности [34]), а при отрицательном делают его менее устойчивым, что приводит в одном случае к уменьшению угла наклона на поверхности, а в другом – к его увеличению, которое ведет к росту второй гармоники). С другой стороны, как показано в [36], при слабых граничных условиях в объеме НЖК может реализоваться полярная деформация. В данном случае подобная ситуация имеет место за счет неэквивалентности поверхностей, которая возникает в результате индуцирования акустическими возмущениями и электрическим полем поверхностных углов θ _σ (– E , a ) ≠ θ _s ( E , a ). Кроме того, сигналы U _1ω и U _2ω независимо от полярности поля достигают своего максимума в окрестности перехода Фредерикса. Уменьшение затем сигналов является следствием развития ЭГД-неустойчивости, структура жидкого кристалла становится мелкодисперсной с волновым вектором q ’ >>  q _2,3 ( q _2,3 – вектор, определяющий ориентационную деформацию), что ведет к подавлению флексоэффекта.

Наряду с рассмотренными причинами изменения значений гармоник U _iω за счет реориентационных механизмов необходимо, по-видимому, учитывать поляризационные эффекты усиления регистрируемых сигналов. В этом случае наведенная ориентационная молекулярная поляризация регистрируется в результате периодической ее модуляции в объеме.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

Подобный эффект может быть зарегистрирован при отсутствии паразитных явлений типа перехода Фредерикса и ЭГДН. Это возможно в ЖК с большой анизотропией диэлектрической проницаемости (ε _α >> 0). Причем, пользуясь аналогией с поверхностной поляризацией, наибольшая величина регистрируемого сигнала должна наблюдаться на второй гармонике, так как U _2ω ~ P_V < θ_d ²> exp( i 2ω t ) ( P_V – объемная поляризация). Исследования подтверждают это предположение: соотношение между гармониками U _1ω ^max: U _2ω ^max<< 1 имеет место во всех изучаемых нематических жидких кристаллах (НЖК). В противоположность этому в смектических жидких кристаллах А- и С- типа U _2ω ~ U _1ω , то есть U _2ω гораздо меньше, чем в нематиках.

Проанализируем подробнее поведение гармоник U _iω в электрическом поле. При приложении поля к гомеотропному слою НЖК, например, ЦФЭГБК ( h = 15 мкм; a = const; ω = 1 кГц) величина U _2ω линейно растет от напряжения U _c вплоть до достижения «насыщения» (рис. 3), которое обусловлено возрастанием стабилизирующего диэлектрического момента над вязкоупругим.

Соответственно, величина U _2ω при этом в 1,5·10³ – 2·10³ раз больше, чем без электрического поля. Если рассматривать зависимости U _2ω от амплитуды возмущения a при фиксированных значениях электрического поля (рис. 4), то следует отметить, что при небольших полях ( Е ≤ 10⁴ В/см) сначала величина U _2ω возрастает, а затем уменьшается вследствие увеличения угла наклона директора относительно нормали к поверхности и перехода к турбулентному движению в слое. При относительно больших полях E ≤ 5·10⁴ В/см такое состояние не достигается.

Величина сигнала U _2ω в этом случае имеет значение ~1 В ( a ~ 1 мкм). В нематической фазе НФООБ и ОЦБ вторая гармоника U _2ω имеет приближенно тот же порядок (рис. 4), хотя в цианобифениле несколько выше, что объясняется, по-видимому, большим дипольным моментом у составляющих его молекул.

Таким образом, в результате приложения электрического поля к гомеотропному слою НЖК в объеме кристалла растет поляризация, факт наличия которой регистрируется посредством ориентационной модуляции и измерения наведенных на проводящих подложках зарядов.

Для исключения альтернативных объяснений возникновения и возрастания U _2ω в полях проводились исследования ее поведения от проводимости σ (механизм ориентационной поляризации – ее анизотропной части), диэлектрической анизотропии ε _α и толщины жидкокристаллического слоя h . Модельные эксперименты проводились на ЦФЭГБК и его смесях с НЖК МББА. При допировании ионными добавками величина сигнала U _2ω уменьшается вследствие, по-видимому, экранизирующего эффекта. Значит, вклад этого механизма пренебрежимо мал (рис. 5 а).

Изменяя анизотропию смесей ε _α > 0 от 20 до 0,05, проводили измерения величины U _2ω при одних и тех же поляризующих напряжениях и возмущении a в зависимости от величины ε _α (рис. 5 б).

Сигнал, обусловленный диэлектрическим механизмом в этом случае будет U _2ω ~ ε_‖ E <θ _d ²>/ε_┴. Согласно этому соотношению, при большой анизотропии ε _α функциональная зависимость U _2ω (ε _α )(при Е = const) выходит на асимптотику – прямую, параллельную оси абсцисс ε _α , а при малых ε _α << 1 величина

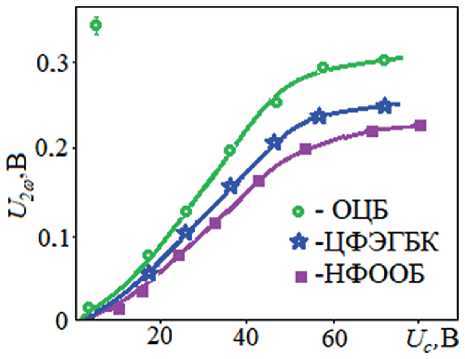
Рис. 3. Полевые зависимости второй гармоники U _2ω в НЖК с ε _α >> 0

( а ≈ 0,3 мкм; h = 15 мкм; ОЦБ при T_N = 35^оС;

ЦФЭГБК при T_N = 48^оС; НФООБ при T_N = 63^оС)

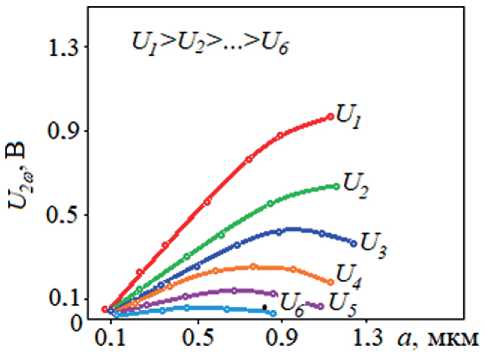
Рис. 4. Зависимости величины второй гармоники U _2ω от амплитуды воздействия при различных поляризующих напряжениях: U₁ = 90 В; U₂ = 60 В; U₃ = 40 В; U₄ = 30 В; U₅ = 20 В; U₆ = 10 В ( h = 15 мкм)

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

а)

б)

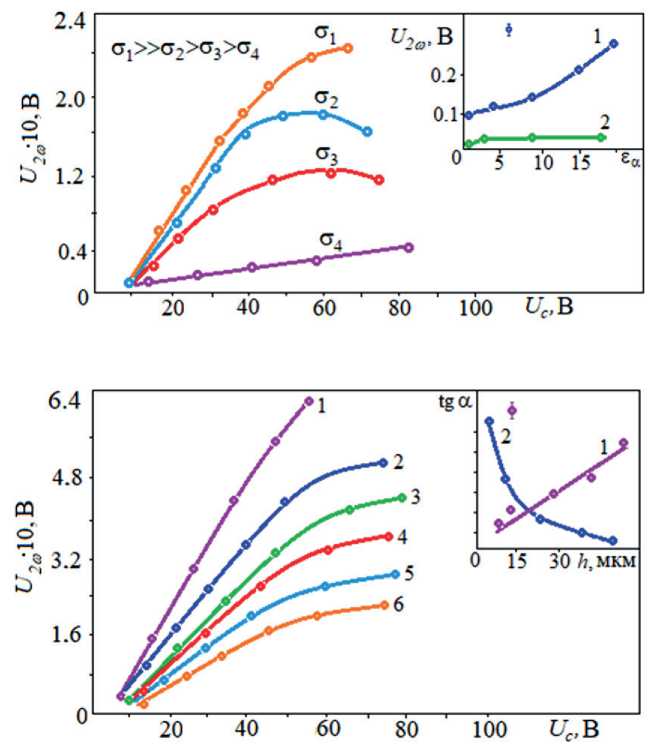
Рис. 5. а) Полевые зависимости второй гармоники U _2ω (ЦФЭГБК) при различной начальной проводимости образцов σ ( a ~ 0,3 мкм; h = 15 мкм); на вставке – зависимости U _2ω от величины диэлектрической анизотропии ε _α (1 – эксперимент; 2 – теория); б) полевые зависимости второй гармоники U _2ω (ЦФЭГБК) при различных толщинах пленок ЖК (1 – h₁ = 70 мкм; 2 – h₂ = 55 мкм; 3 – h₃ = 45 мкм; 4 – h₄ = 30 мкм; 5 – h₅ = 15 мкм; 6 – h₆ = 10 мкм); на вставке – зависимости тангенса угла наклона кривой U _2ω ( U _c ) от толщины h (1 – эксперимент; 2 – теория)

сигнала будет стремиться к нулю, как изображено на рис. 5 б. В противоположность этому на практике величина сигнала U _2ω при ε _α << 1 не стремится к нулю, а при ε _α >> 1 не выходит на упомянутую асимптотику. Но очевидно, что вклад диэлектрической проницаемости не равен нулю и по оценкам составляет порядка 10–15% от регистрируемого значения U _2ω . Результаты проведенных измерений величины второй гармоники от толщины слоя НЖК (рис. 5 б) показали, что тангенс угла наклона зависимости U _2ω к оси абсцисс U _c увеличивается с толщиной h , тогда как при механизме диэлектрической модуляции величина tg α ~ h^–1 (так как U _2ω ~ E = U / h , то tg α ~ U _2ω / U ~ h ^–1).

Обсудим теперь поведение первой гармоники в электрическом поле. Подробно изучен ЦФЭГБК. Зафиксируем амплитуду возмущения, например, a ~ 0,3 мкм и проанализируем при этой деформации зависимость U1ω(Uc) (рис. 6).

При малых поляризующих напряжениях U _c ≤ 15 B ( h = 15 мкм) зависимость U _1ω аппроксимируется степенной функцией типа U_cⁿ (где n ~ 3); при U _c >> 15 B вторая гармоника U _2ω зависит как U _c ^–1. Качественно такое поведение можно объяснить изменением амплитуды колебания директора, что следует из формулы для разности фаз:

2тт f^/2             2ттй

8 = — I   An(z)dz =—— < An(z) >,     (5)

^-h/2

где <∆ n ( z )> – усреднение по толщине слоя кристалла; h – толщина ЖК; λ – длина волны света.

Если учесть в исходных уравнениях слагаемое, описывающее действующее поле ε _α ( En )²/4π, тогда

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

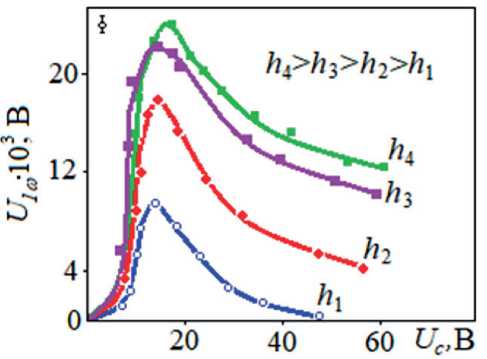
Рис. 6. Полевые зависимости первой гармоники U _1ω при различной толщине образцов h ( a = const, ω = 1 кГц): h₁ = 15 мкм; h₂ = 30 мкм; h₃ = 45 мкм; h₄ = 55 мкм (ЦФЭГБК)

для амплитуды девиации директора ЖК можно приближенно записать [34]:

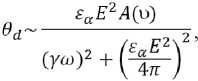
где A( υ ) – функция скорости колебания одной из поверхностей и объемных градиентов υ( z, r ) .

В этом случае величина сигнала первой гармоники U _1ω пропорциональна толщине ЖК и углу девиации его директора U _1ω ~ e ₁₁ hθ_d , то есть при условии γω >> ε _α E ²/4π (малые поля) будем иметь степенную зависимость U _1ω ~ U _c ³. В случае, когда γω < ε _α E ²/4π, имеем U _1ω ~ U _c ^–1 .

Таким образом, в малых полях величина сигнала растет за счет усиления амплитуды колебания директора, но при некотором критическом поле E = (4πγω/ε _α )^1/2 происходит его подавление, так как слой стабилизируется постоянным электрическим полем.

Ранее было установлено [8, 9, 12, 13, 16, 22, 25, 28], что при периодических сдвиговых колебаниях одной из ограничивающих жидкий кристалл подложек в слое кристалла возникает ЭДС, обусловленная как механизмом флексоэлектрической поляризации, так и механизмом модуляции поверхностной поляризации акустическими колебаниями. В данной статье будем рассматривать влияние внешнего электрического поля E на поведение первой U1ω и второй U2ω гармоник, индуцируемых сдвигом. В общем случае поведение первой гармоники в изучаемых веществах аналогично поведению U1ω, возбужденной изгибны-ми колебаниями одной из поверхностей жидкого кристалла. Однако имеются в полевых зависимостях Uiω и свои специфические особенности, связанные с симметрией возмущения и его пространственной локализацией.

Согласно решению для распределения угла отклонения директора от нормали к ячейке θ по координате в z общем виде можно записать:

„ P^UO                _      v- _z _      .

6=--exp —— q(z-S) cos — q(z-S) costot, (7)

где η ₁ – коэффициент вязкости; q – реальная часть корней характеристического уравнения; ρ – плотность заряда; S – расстояние, на котором директор отклоняется от положения равновесия; ω – частота колебаний; υ _o – скорость при z = 0.

Колеблющийся электрод является источником быстро затухающей упруго-вязкой волны с волновым вектором | q | >  h ^–1 ( h – толщина реально изучаемых слоев 10 ≤ h ≤ 100 мкм). Например, в НЖК МББА при начальной гомеотропной ориентации молекул в объеме слоя ЖК распространяется возмущение с волновым вектором | q | ~ 3·10³ см^–1, что составляет пространственный масштаб их локализации порядка 3·10^–4 ÷ 5·10^–4 см, а это значение меньше толщины жидкого кристалла ( h ≈ 20 мкм). Отсюда следует, что при слабых граничных условиях можно считать, что основную роль будут играть ориентационные поверхностные возмущения.

Рассмотрим полевые зависимости первой U _1ω и второй U _2ω гармоник при малых напряжениях смещения, например, в нематических жидких кристаллах МББА и ЦФЭГБК (рис. 7), причем будем варьировать знак поля относительно направления градиента колебательной скорости ∂υ _x /∂z. Этот гра-

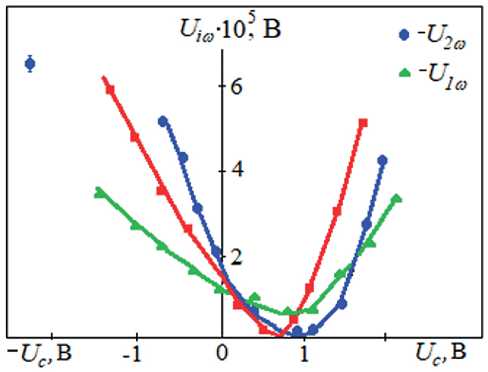
Рис. 7. Полевые зависимости величин первой U _1ω и второй U _2ω гармоник при малых поляризующих напряжениях (сплошные линии – МББА при T_N = 24^oC; пунктирные линии – ЦФЭГБК при T_N = 48^oC)

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ диент не параллелен вектору нормали к поверхности колеблющейся пластины–подложки.

Отметим, что положение минимумов величин первой U _1ω и второй U _2ω гармоник не совпадает с нулевой точкой по оси абсцисс, когда U _c = 0. Величины гармоник U _1ω и U _2ω имеют максимум тогда, когда на подвижный электрод подается положительный потенциал. Отметим также, что характерное поляризующее напряжение U _c ~ +1 В, при котором значения гармоник U _1ω и U _2ω минимальны.

Обсудим поведение составляющих гармоник U _iω в рамках подхода, обозначенного ранее. Для этого разберем сначала поведение второй гармоники сигнала U _2ω . В отсутствие поля величина второй гармоники согласно формуле

U 2ω = ∫ 0 ^h P s ( z )( ) <θ d ²> dz = P s S <θ d ²> cos<θ o > =

= U_s cos<θ _o ><θ _d ²>, (8)

(где P_s – величина поверхностной поляризации; U_s = P_s S – падение напряжения на поверхностном слое; <θ _o > – среднее значение стационарного угла наклона директора; <θ _d ²> – квадрат среднего значения угла, характеризующего осцилляции директора) пропорциональна углу наклона директора на поверхности <θ _o > и величине поверхностной поляризации P_s , вектор которой имеет определенное направление относительно подложки. Последнее и является причиной асимметрии в полевой зависимости U _2ω .

В случае если направление внешнего поля совпадает с направлением поверхностной поляризации, то общий регистрируемый сигнал:

U 2ω ~ S эф P s <θ d ²> – P V S ^–2<θ d ²>, (9)

где S _эф – эффективная толщина поверхностной поляризации; P_V – индуцированная внешним полем ориентационная поляризация.

Или можно записать проще:

U 2ω ~ U s <θ d ²> – U n ( Sh )^–1<θ d ²>. (10)

Отсюда ясно, что при возрастании внешнего поляризующего напряжения величина второй гармоники U _2ω будет иметь минимум. В противоположном случае, когда P_s и P_V имеют одно и то же направление, сигнал U _2ω увеличивается, что подтверждается экспериментом.

В частности, этот результат позволяет определить направление ориентации молекул поверхностного слоя – поверхностной поляризации – и оценить по положению минимума падение напряжения U _δ на этом поляризованном слое. В случае НЖК МББА молекулы направлены своим отрицательным концом к поверхности, а величина U _s ~ 1 В. Для НЖК

ЦФЭГБК U _s ~ 0,7 В, а молекулы этого кристалла также направлены своим отрицательным концом к поверхности.

Асимметрия сигнала первой гармоники U _1ω тесным образом связана с наличием поверхностной поляризации. Решение этой задачи представляет значительные трудности и, в общем случае, нелинейно [31]. Однако можно показать, что уже в линейном приближении такая асимметрия возникает. Так как возмущение локализовано у поверхности колеблющегося электрода, то воспользуемся моментными условиями на поверхности [36]:

W (<θ _d > – <θ _o >) + k (∂<θ _d >)/∂z =

±( e ₃₃ P_s ) E ,                                       (11)

где e ₃₃ – флексоэлектрический коэффициент. Знаки выбираются в зависимости от направления поля относительно подложки и направлением вектора поляризации. Считаем, что θ мал и <θ _d ><< <θ _o > (<θ _d > – угол колебаний директора на поверхности). Тогда в (11) можно подставить приближенное решение типа (7), когда θ _d ~ θ _d ’ exp( iqz ). Отсюда получим при z = 0 для угла:

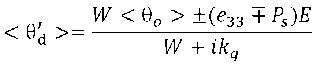
или при k_q >  W :

-

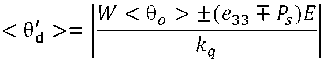
Из этого выражения следует, что величина угла колебания директора будет существенным образом зависеть от соотношения величины флексоэлектрического коэффициента e ₃₃ , величины поверхностной поляризации P_s , а также знака поля. То есть в одном случае ЖК-структура стабилизируется, в другом случае она менее устойчива к внешним возмущениям.

Применительно к конкретному случаю, например, к нематическому жидкому кристаллу МББА, будем иметь следующую картину. Так как дипольные молекулы направлены своим отрицательным концом к поверхности, то в случае, когда на поверхности положительный потенциал, получаем:

d > ~ W o > + ( e 33 - P s ) El,                (14)

а при отрицательном:

d > ~ | w o > + ( e 33 - P s ) E |,                 (15)

Таким образом, в области положительных напряжений смещения молекулы стабилизируются, а при отрицательных напряжениях молекулы менее

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ устойчивы к ориентационным возмущениям, при условии |e33| < |Ps|.

Перейдем теперь к рассмотрению поведения регистрируемых сигналов первой U _1ω и второй U _2ω гармоник при больших поляризующих напряжениях. Поведение первой гармоники U _1ω в этом случае аналогично поведению первой гармоники, возбуждаемой при изгибных колебаниях [8, 9, 12, 16], поэтому самостоятельного интереса этот вопрос не имеет.

Остановимся подробнее на изучении влияния внешнего электрического поля на величину и изменения второй гармоники. Исследование будем проводить на примере НЖК ЦФЭГБК. Отличительной особенностью влияния электрического поля E в случае сдвиговых колебаний является то, что максимальной величины вторая гармоника U _2ω достигает в низкочастотной области ω ~ 100 Гц (рис. 8), тогда как при изгибных колебаниях частотная регрессия второй гармоники начинается в килогерцовом диапазоне.

Из частотной зависимости U _2ω (ω) (υ = const) следует, что величина второй гармоники U _2ω резко уменьшается с частотой возмущения (рис. 8). Например, величины второй гармоники при ω ~ 100 Гц и при ω ~ 750 Гц при данном значении напряжения смещения отличаются в 5·10² раз. Возможной причиной такого изменения является локализация ориентационного возмущения у колеблющегося электрода с увеличением частоты. Так как изначально согласно уравнению [35] разность фаз:

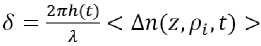
(где h – толщина ЖК-слоя; λ – длина световой волны) волновой вектор возмущения | q | >  h ^–1 и с увеличением частоты характерная область возмущения S ~ | q |^–1 ~ ω^1/2 на частоте 1 кГц сможет составлять S ~ 10^–4 см.

Последнее подтверждается исследованием частотной зависимости величины второй гармоники оптического сигнала I _2ω / I_o при одновременном действии поляризующего напряжения (рис. 8). Акусто-оптический эффект, заключающийся в модуляции светового потока, поляризованного в свете, прошедшего через ячейку, сильно ослабляется с увеличением частоты ω, а при частоте ω ~ 1 кГц не наблюдается вовсе.

ЗАКЛЮЧЕНИЕ

Таким образом, в статье экспериментально исследовалось влияние действия электрического поля на поверхностную поляризацию, возникающую вследствие флексоэлектрического эффекта. Выявлено, что гармоники флексоэлектрического сигнала зависят от направления электрического поля, при приложении положительного потенциала к подвижной пластине они принимают меньшие значения, чем при отрицательном. При действии слабых полей величина сигнала на частоте возбуждения прямо пропорциональна амплитуде осцилляций директора жидкого кристалла и возрастает за счет ее увеличения.

Теоретически обосновано, что при слабых граничных условиях основную роль играют ориентационные поверхностные воздействия. Знак элек-

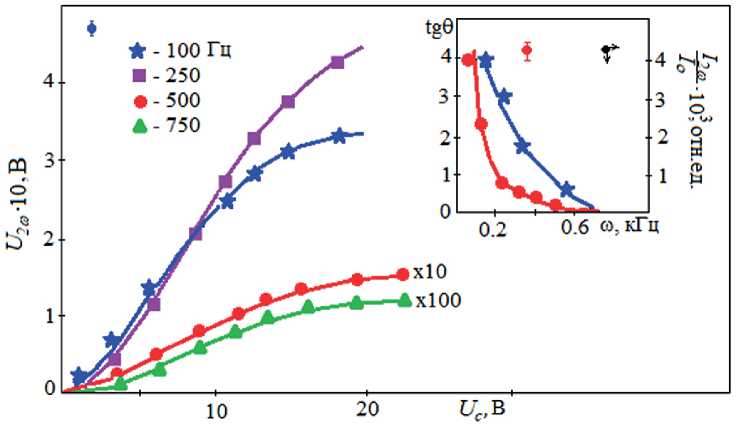
Рис. 8. Полевые зависимости величины второй гармоники U _2ω при различной частоте возмущения ω (ЦФЭГБК при T_N = 48^oC); на вставке – частотные зависимости тангенса угла наклона tgθ и величины акустооптического эффекта I _2ω / I_o .

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ трического поля можно варьировать относительно направления градиента колебательной скорости. Обнаружено, что значения первой и второй гармоник принимают максимум при приложении на подвижный электрод положительного потенциала. Характерное поляризующее напряжение, при котором U1ω и U2ω гармоники минимальны, составляет Uc ~ +1 В. Асимметрия зависимости U2ω от приложенного поля объясняется пропорциональностью углу наклона директора на поверхности <θo> и величине поверхностной поляризации Ps. Также обнаружено, что молекулы ЖК (МББА и ЦФЭГБК) направлены отрицательным концом к поверхности подложки ячейки.

Полученные результаты исследований можно использовать при разработке датчиков давления, сейсмодатчиков для зданий и сооружений, модуляторов света, а также акустооптического затвора для стеклопакетов.