Alfv'en waves in the magnetosphere generated by shock wave / plasmapause interaction

A considerable part of geomagnetic pulsations observable in Earth’s magnetosphere are related to the generation mechanism known as “field line resonance” (FLR). In particular, resonant Alfvén oscillations can be generated by fast magnetosonic (FMS) wave pulses caused by interplanetary shock waves propagating in the magnetosphere [Allan et al . , 1986] .

This interpretation explains well the generation of Alfvén waves with toroidal polarization in the magneto- sphere [Leonovich, Mazur, 1989; Kozlov, 2010]. If the magnetospheric plasma in such a model is inhomogeneous in the meridional plane (along the magnetic field lines and across the magnetic shells), but homogeneous in the azimuthal direction, then all its oscillations can be regarded as an expansion in harmonics of the form ~exp(imφ–iωt), where m=0, ±1, ±2, … is the azimuthal wave number, φ is the azimuthal angle, ω is the wave frequency.

Toroidal Alfvén oscillations are excited by azimuthally large-scale FMS waves (with m~ 1). These FMS

А.С. Леонович, Цюган Цзун, Д.А. Козлов, Юнфу Ван waves can penetrate deep into the magnetosphere from the solar wind. Poloidal Alfvén waves are azimuthally small-scale ( m ≫ 1). The azimuthally small-scale FMS waves incident on the magnetosphere from the solar wind are reflected by the magnetopause, thus failing to penetrate into the magnetosphere [Leonovich, Mazur, 2000; Cheremnykh et al., 2016] . The FMS waves that do penetrate into the magnetosphere are therefore believed to be likely to excite only toroidal Alfvén waves in it [Leonovich, 2001; Chelpanov et al., 2018] .

After interplanetary shock wave passage, Alfvén waves with toroidal polarization are often observed inside the magnetosphere [Potapov, 2013] . They are generated by the field line resonance mechanism. A number of studies based on spacecraft observations have demonstrated, however, that Alfvén waves with poloidal polarization can also be excited inside the magnetosphere after shock wave passage [Zong et al., 2009; Liu et al . , 2013] . Poloidal waves inside the magnetosphere are most often generated by unstable high-energy particle fluxes [Dai et al., 2013] . Sometimes (in 10–15 % of cases), however, Alfvén waves with both the toroidal and poloidal polarization are excited near the plasmapause, after an interplanetary shock wave front passes through the magnetosphere. In the preceding time interval, high-energy particle fluxes, which could be considered as a potential source of the poloidal waves, are absent from the observation region [Zong et al . , 2017] .

In this paper, we propose a new concept for the po-loidal Alfvén wave generation in the magnetosphere by an interplanetary shock wave front. We suggest that the shock wave front penetrates the magnetosphere and interacts with the plasmapause. In their contact region, a fast magnetosonic wave packet arises which then generates Alfvén waves at resonance magnetic surfaces. We calculate the total field of Alfvén oscillations in the vicinity of the plasmapause using a cylindrical model of the magnetosphere.

• 1.    OBSERVATIONS

• 2.    MEDIUM MODEL

AND POSSIBLE SCENARIO

An example of such observations is shown in Figure 1. The measurements were carried out by the CLUSTER C3 spacecraft, which was in the vicinity of the plasmapause at that time. Figure 1 contains 5 panels ( a – e ). The top ( a ) panel illustrates the behavior of the integral flux of high-energy ( E >50 keV) electrons before and after the shock front passage. The behavior of the electric and magnetic components of the Alfvén oscillation field is presented on two panels ( b , c ): ( b ) for the poloidal ( B r , E a ) and ( c ) for the toroidal ( B a , E r ) modes. Panel ( d ) shows the behavior of the magnetic field z -component. The magnetic and electric fields are projected onto a local mean-field-aligned (MFA) coordinate system, in which the parallel direction p is determined by the 15-min sliding averaged magnetic field, the azimuthal direction a is parallel to the cross product of the p and the spacecraft position vector, and the r completes the triad. Panel ( e ) of Figure 1 shows the cold plasma density deduced from the potential as measured by CLUSTER C1, C2, and C4. There was a gap in the C3 spacecraft potential data, but all the four spacecraft are quite close to each other in this case. We use the method proposed by Moullard et al. [2002] to cal-

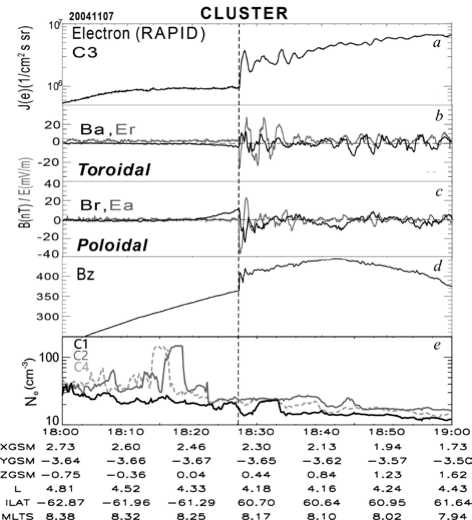
Figure 1. CLUSTER C3 measurements of ULF waves and energetic electron flux perturbations induced by an interplanetary shock on November 7, 2004: the integral flux of energetic electrons (E>50 keV) measured by RAPID onboard C3 (a); the toroidal mode wave magnetic field Ba and electric field Er (b); the poloidal mode wave magnetic field Br and electric field Ea (c); the magnetic field Bz component from C3 (d); the cold plasma density Ne deduced from spacecraft potential measured by CLUSTER C1, C2, and C4 (e). The position in GSM, L value, invariant latitude (ILat) and magnetic local time (MLT) for C3 are shown at the bottom. The vertical dashed line shows the arrival time of the interplanetary shock culate the density from the spacecraft potential. We can see that the cold plasma density is ~20 cm–3, the typical value near the plasmapause.

It is evident from Figure 1 that after the shock front passage both modes of Alfvén oscillations are excited: poloidal and toroidal. After that, the poloidal component amplitude of the oscillation field decays rather quickly, while the toroidal component amplitude remains almost unchanged. At the same time, the high-energy electron flux begins to increase. Zong et al. [2017] suggested that poloidal Alfvén waves interact with the plasma electrons, transferring their energy to them.

The question remains as to the source of the poloidal Alfvén waves themselves. We suggest the following generation scenario for such poloidal Alfvén oscillations generated by shock wave passage through the magnetosphere. When the shock wave front interacts with the plasmapause, a localized perturbation arises in their intersection region. A narrowly localized FMS wave packet contains harmonics capable of effectively exciting both toroidal and poloidal Alfvén waves. Using the cylindrical model of the magnetosphere, we calculate the field of Alfvén oscillations generated in the magnetosphere by such a secondary source and determine sectors, where the poloidal magnetic field component dominates in the generated Alfvén oscillations.

We consider the generation of Alfvén waves by an FMS wave packet in the near-equatorial region of the real

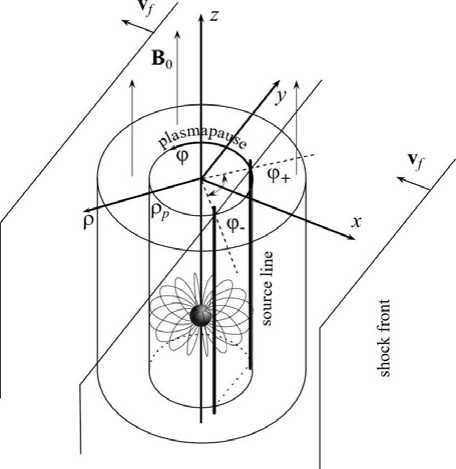
Figure 2 . Diagram of shock front passage through the plasmasphere in the cylindrical model of the magnetosphere. The source of the resonant Alfvén waves (FMS pulse propagating along the plasmapause) is stretched along the shock front/plasmapause intersection lines (source lines)

the outer magnetospheric regions. A characteristic value of v _Ap= 1000 km/s (average between the minimum and maximum) was therefore chosen in the plasmapause transition layer, and v _Am=300 km/s in the outer magnetosphere. In our subsequent studies, we plan to examine a similar problem in a more complex model of the plasmapause transition layer, including a nonmonotonic distribution v A (ρ) in it.

3. ANALYTICAL DESCRIPTION

Within the ideal MHD framework, we can obtain a system of equations describing interacting linear Alfvén and FMS waves in a cylindrical coordinate system by expressing the transverse (relative to the background magnetic field) component of the disturbed electric field E _± via scalar and vector potentials ф and у =(0, 0, у) [Leonovich, 2001]

Е _±=7_±ф + [ 7_±х у ] .

For an individual wave field harmonic of the form ~ exp( — i to t + im y + ik_zz ) (where и is the frequency, m is the azimuthal wave number, and k z is the wave-vector z -component) the equation for the Alfvén mode excited by an FMS source is

magnetosphere, using a model plasma cylinder with an axial magnetic field (Figure 2). We employ a cylindrical coordinate system (ρ, φ, z ). The plasma is assumed to be inhomogeneous in the ρ coordinate. FMS wave pulses generated by shock wave at the plasmapause have the form of a straight line moving along the surface together with the shock front (source lines, Figure 2).

We use the following model for the equatorial Alf-vén speed profile over the radius:

d      d    m2

VPKа — ф —   Kaф = imto    V, dp    dp    pdp where ф and V are Fourier harmonics,

2 A

to ²

v

2 A

—

_kz 2_.

v A =

P p

2 P

p pp vAm + vAp - ( vAm - vAp ) tanh “Г-- Δp

The components of the disturbed magnetic field are expressed via the potentials as follows:

B p

where v _Am, v_{A p} are the characteristic magnitudes of the Alfvén speed in the outer magnetosphere and in the plasmasphere respectively, ρ p and Δ p are the mean radius and thickness of the plasmapause. The following parameter values were chosen: v Am =300 km/s, v Ap =1000 km/s, ρ p =4 R E (where R E is the Earth radius), Δ p =0.6 R E .

Note that in the real magnetosphere the Alfvén velocity profile near the plasmapause has a “knee” with a local minimum value of ~100–300 km/s at the inner plasmapause boundary and a local maximum value of ~800–1200 km/s in the outer magnetospheric region adjacent to the plasmapause [Kim et al . , 2018] . However, in order to avoid unnecessary complications in the calculations, we use simpler model (1) for the v A (ρ) distribution near the plasmapause, where the v A profile is described by a simple transition layer.

The model takes into account the following features of the plasma distribution in the real magnetosphere. The Alfvén velocity decreases, on average, in the direction from Earth to the magnetopause, which is reflected on the common factor ρ^–1. Moreover, the model Alfvén velocity distribution has a sharp jump in the v A value near the plasmapause, from v A ~1500–2000 km/s, typical of the plasmasphere, to v A ~200–400 km/s, typical of

.. c [ m d _ ]

= ik_z —I — Ф — i "^V I ;

to ^ p dp )

B _Ф

B z

c | . d m _ ] = ik _z —I i —ф +— v I ;

to( dp p )

c f 1 d d _ m ²_) = ^l-\ ^-^p^V rV | .

to (p dp dp p )

Assuming that the FMS wave field (potential ψ) results from nonlinear interaction of the shock front and the plasmapause, we cannot determine it using linear theory and will use the following model expression for propagating pulses instead:

v ( p , Ф , t ) =

= V o 6 ( t ) 0 ( t p ^— t ) R ( p ^— p p ) F ( ф ^— Ф ± ( t ) ) ,

where ψ 0 is the amplitude of the FMS pulse propagating along the plasmapause, θ( t ) is the step function (θ( t )=0 when t <0, 9( t )=1 when t > 0), R ( p ) and F (ф) are the functions narrowly localized in the ρ and φ coordinates respectively, t _p is the time interval within which the shock front stays in contact with the plasmapause and φ ± are the azimuth angles of source lines (intersection lines of the shock front and the plasmapause surface). If the shock front moves at velocity v f (see Figure 2) and at

moment t= 0 first comes into contact with the plasmapause boundary, then tp = 2 * vf

The azimuths of the two source lines moving along the plasmapause when 0≤t≤tp are ф±(t)=

± arccos 1

—

v _f t

A

V

P p J

We use the following models for the functions R (ρ–ρ p ) and F ( ф —ф ± ( t ) ) :

R ( p ^— P p ) =

^A p       _;

( p ^— P p ) 2 + ^A 2’

F ( ф —ф ± ( t ) ) =

^А ф

2, (ф —ф±( t)) + Аф where parameters Δρ and Δφ describe the localization area of the FMS pulse.

The individual harmonic ф in the right-hand side of

(2) is related to the source function (4) by

(N

ф ( р , m , ю ) =

3 L” e " t dt j- ,* Ф , t ) e "m ^Ф d Ф ,

ф ( р , ф , t ) =

( 2 П ) ¹/²

”

T e im ^Ф ! _— „ Ф ( Р , m , ® ) e

—”

—

i ^ю t d ю.

The solution describing the total field of resonant Alfvén oscillations excited by source (4), may be obtained from the solutions of (2) using inverse Fourier transform (5). It has the form [see Zong et al., 2018] :

ф (p, ф, t) = —0^1 Tme i™Apt mАф sinmф x np m=i e‘mApt(1 *£p)cos (mф (t′)) ---------, V 5        dt ′ x min(t,tp )

^x j 0

^{+ T} m.

i m a t '( p ^— P p + i A p )

xf

e ^a

------ d t ′

' + Tm where ωA=kzvA(ρ) is the local frequency of resonant Alfvén oscillations with longitudinal wave vector kz on the magnetic shell with radius ρ; ωAp=ωA(ρp) is the Alfvén oscillation frequency at the plasmapause; a = —2 (d In vA / dp) is the characteristic scale of the function vA(p) near the resonance shell, ep = toAAp / mAp a;

^T m = ma ( P ) /P® A ( P ) , Ф 5 =Ф + ⁽ t )•

When calculating the integral over time t' , the upper limit is restricted to the current time t. This is due to the causality principle: the oscillation field at a given point, at time t, is determined by the source function over the entire preceding time interval. A formal justification for this condition can be found in [Leonovich, Mazur, 1998] . Using formulas (3) and (6), we can calculate numerically the magnetic field of resonant Alfvén oscillations with given longitudinal wave vector component k z .

4. RESULTS OF NUMERICAL CALCULATIONS

AND DISCUSSION

Let us consider the distribution of magnetic field components of Alfvén waves excited by FMS pulses moving along the plasmasphere. Figures 3 shows the spatial distribution of the toroidal ( B φ ) and poloidal ( B ρ ) components of the disturbed magnetic field for the fundamental harmonic of Alfvén oscillations, N = 1 (with k z = k z 1 =π/ L , where L ≈2.3ρ p is the field line length in a dipole magnetic field connecting its two intersection points with the ionosphere) at different moments of time across a section of the cylinder. For numerical calculation we have chosen the following localization parameters for FMS pulses: Δρ=0.3 R E , rad, shock front speed v f =500 km/s. Note that the coordinates ( x , y ) used in Figure 3 do not correspond to the coordinates ( x GSM , y GSM ) in Figure 1. The coordinate system ( x , y ) is tied to the shock front/plasmapause first contact point.

Figure 3, a shows the distribution of the oscillation field corresponding to the moment t =0 . 05 t p . The top panel shows the distribution of the disturbed component B _p ; the middle panel, that of the disturbed component B _φ; and the bottom panel, the ratio of their magnitudes, r _pt=| B φ|/| B ρ|. Figure 3, b presents the distributions of the same parameters for the moment t =1 . 1 t p . The ratio r _pt allows us to determine the polarization of the oscillations. The Alfvén oscillations can be conventionally referred to as poloidal for r pt < 1 , or toroidal for r pt > 1 .

In the region located near the FMS pulses the amplitude of the toroidal component of the magnetic field is much larger than that of the poloidal one. However, even in this region there always exists an area where the generated Alfvén oscillations have a poloidal polarization. This is possible because the toroidal component of magnetic field B _ф is proportional to У_фф , while the po-loidal component B _p is proportional to У_рф . Oscillations of the poloidal and toroidal components are phase-shifted in the azimuthal direction. Thus, an area exists in the region of the FMS pulse location, where the amplitude of the toroidal component passes through zero and the amplitude of the poloidal component has a maximum. Therefore, in the region near the source location there always exist adjacent sectors dominated by either toroidal or poloidal magnetic field components.

The distributions in Figures 3, a , b demonstrates another feature of Alfvén oscillations. Alfvén waves always have poloidal polarization in both the region of the first shock front/plasmapause contact (φ=0) and in the region where the contact is lost (ф= ± n). This follows directly from the form of solution (6). All azimuthal harmonics of the toroidal component of Alfven oscillations have a zero amplitude at these points ( ~ sin( m φ)). If such is the case also in the real magnetosphere, this feature of the Alfvén oscillation distribution can be used to determine the sector of the first shock front/plasmapause contact. Note that the position of this sector is determined by the propagation direction and the inclination of the shock front and may differ substantially from the noon-midnight meridional crosssection of the magnetosphere.

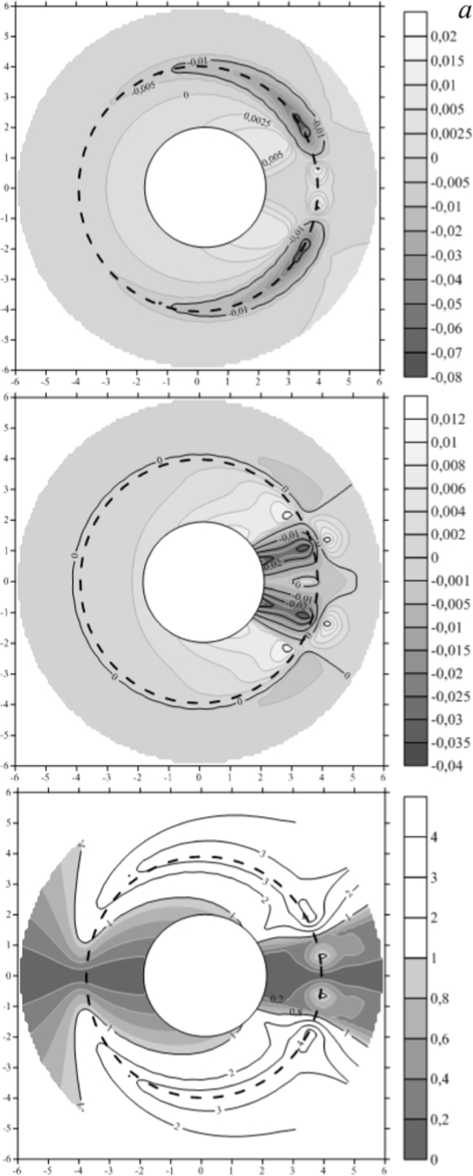
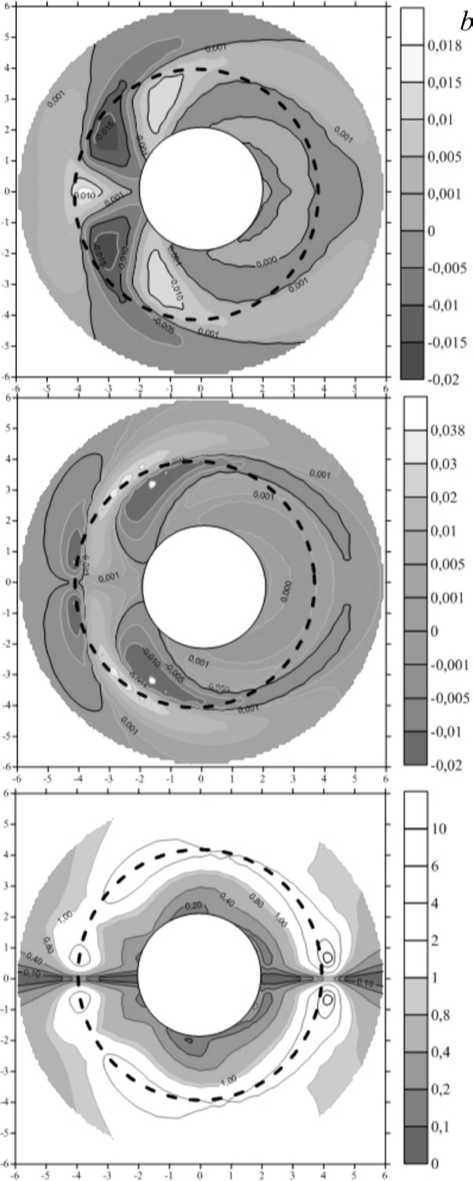
Figure. 3 . Distribution of the resonant Alfvén oscillation field in the ( x , y ) plane perpendicular to the Z axis at time moments: t =0.05 t _p ( a ) and t =1.1 t _p ( b ). The top panels show the distribution of the magnetic field poloidal component Re( B _ρ); the middle panels, the distribution of the toroidal component Re( B _φ); the bottom panels, the ratio r _pt = | B _φ|/| B _ρ| determining wave polarization. Shades of gray show sectors with poloidal polarization of Alfvén waves ( r _pt < 1)

Based on these calculations, the following interpretation can be given for the data in Figure 1. When the shock wave arrived at the plasmapause, CLUSTER C3 was located in the sector, where the amplitudes of po-loidal and toroidal oscillation components were comparable to each other. The spacecraft then left the sector dominated by the poloidal component, which no- ticeably decreased. At the same time, the high-energy (E>50 keV) electron flux began to grow. This growth can be explained as follows. It is known that the toroidal Alfvén waves decay strongly in the plasmapause transitional layer due to their interaction with background plasma electrons [Leonovich, Mazur, 1989]. The phase velocity of Alfvén waves in this region becomes equal to the thermal velocity of electrons, which leads to Cherenkov resonance between them, resulting in electron heating.

The study by A.S. Leonovich and D.A. Kozlov (Sections 2 and 3) was performed with budgetary funding of Basic Research program II.16.