Альфвеновские волны при начальном возмущении в БМЗ-волноводе

Мы рассматриваем в настоящей работе эволюцию возмущения, имеющего место в некоторый момент времени в области, расположенной вблизи поверхности, где альфвеновская скорость имеет минимум в направлении поперек магнитного поля. В такой области имеются условия для волноводного распространения БМЗ-волн, поэтому начальное возмущение приводит к появлению БМЗ-возмущения, распространение которого по координате в направлении неоднородности ограничено. В направлении двух других координат возмущение распространяется свободно. Вследствие наличия связи БМЗ и альфве-новских волн волноводное возмущение постепенно трансформируется в альфвеновские волны и по истечении некоторого периода времени распространяется уже в виде альфвеновского возмущения.

МГД-возмущения, эволюция которых развивается по такому сценарию, могут иметь место в хвосте магнитосферы. В его центральной части имеются условия для локализации БМЗ-волн в поперечном направлении, поэтому хвост можно рассматривать как вытянутый вдоль магнитного поля БМЗ-волновод [Allan, 1998; Allan, Wright, 2000; Mills, Wright, 2000; Lysak, 2009; Mazur et al., 2010]. Возмущения, связанные с различными процессами в дальней части хвоста (например, теми процессами, которые связаны с пересоединением), могут возбуждать БМЗ-волны. БМЗ-волны, распространяясь вдоль волновода, трансформируются в альфвеновские волны, которые достигают Земли, вызывая возмущения геомагнитного поля и высыпания частиц [Wright, Allan, 2008]. Аналогичные возмущения могут иметь место также в солнечных стримерах [Deforest, Gurman, 1998; Verwichte et al., 2005].

Мы полагаем, что начальное возмущение локализовано вблизи оси волновода, и рассмотрим образование альфвеновского возмущения там, где имеет место резонанс между БМЗ-волнами и альфвеновскими волнами, т. е. в области непрозрачности для волноводного возмущения. Предполагается, что в этой области начального возмущения нет, поэтому альфвеновские возмущения возбуждаются в результате трансформации волноводного БМЗ-возмущения, а вызванные непосредственно начальным возмущением отсутствуют.

Сначала мы рассматриваем эволюцию волноводного возмущения. Как известно [Uberoi, 1972; Tataronis, Grossmann, 1973; Grossmann, Tataronis, 1973; Zhu, Ki-velson, 1988], волноводные моды, если пренебречь связью БМЗ и альфвеновских волн, обладают дискретным спектром действительных частот. В таком приближении начальное возмущение должно представляться в виде суммы мод, амплитуды которых постоянны во времени. Однако известно, что при учете связи БМЗ и альфвеновских волн спектр волноводных мод становится непрерывным, а дискретные частоты выделяются только при t →∞ [Tataronis, Grossmann, 1973; Grossmann, Tataronis, 1973; Zhu, Kivelson, 1988]. В настоящей работе связь БМЗ и альфвеновских волн предполагается слабой вследствие малости волновых чисел, соответствующих координате y (в системе координат: x – вдоль направления неоднородности, z – вдоль невозмущенного магнитного поля). Слабость связи БМЗ и альфвеновских волн приводит к медленности резонансной трансформации БМЗ-волн в аль-фвеновские, т. е. к малости декремента БМЗ-волн по сравнению с их частотой. Мы показываем, что в этом случае фурье-образ БМЗ-возмущения (по координатам, вдоль которых плазма однородна) можно представить в виде суперпозиции коллективных мод главного по связи БМЗ и альфвеновских волн приближения. Это моды, частоты и структура по x-координате которых совпадают с частотами и структурой волноводных мод, получаемых без учета связи БМЗ и аль-фвеновских волн. Декремент таких коллективных мод вычисляется методом возмущений.

В координатном представлении волноводное БМЗ-возмущение, вызванное начальным возмущением произвольной пространственной структуры, представляется в виде суперпозиции пакетов коллективных мод, каждый из которых состоит из мод с одним номером. Поэтому мы далее получаем аналитическое описание пространственно-временной эволюции альфвеновских возмущений, производимых такими волноводными пакетами. Для этого мы используем решение уравнения, описывающего трансформацию БМЗ-возмущения в альфвеновское возмущение на языке фурье-образов этих возмущений. Из этого решения посредством обратного преобразования Фурье находим альфвеновское возмущение, в которое трансформируется отдельный волноводный пакет.

Полученные для пространственно-временной эволюции альфвеновского возмущения формулы описывают связь параметров альфвеновского возмущения с параметрами начального возмущения и параметрами, задаваемыми условиями резонанса, – резонансным волновым числом и шириной резонанса по продольным волновым числам. С их использованием проводится анализ зависимости пространственно-временной структуры альфвеновского возмущения, в которое трансформируется отдельный волноводный пакет, от соотношения масштабов начального возмущения и резонансных масштабов.

Исходные уравнения

Обозначим через B ₀ невозмущенное магнитное поле. Будем предполагать, что оно однородно и направлено вдоль оси Z. Будем предполагать, что невозмущенная концентрация n ₀ неоднородна в направлении x . Тогда альфвеновская скорость V_a = Bq /(4 n mn₀ ) ^1/2 также неоднородна в направлении x . Обозначим: B – возмущение магнитного поля, v – скорость плазмы в возмущении. Будем рассматривать волны с заданным волновым числом k y .

Линейные МГД-возмущения описываются уравнениями

V V t d t v , -d z d z v , =d , _V ,

V <  t d t V y -d z d z V y = ik y v ,                       (1)

V = div v = d _xV_x + ik y v y .

Осуществим переход к безразмерным переменным и функциям с использованием каких-либо параметров размерности длины L и размерности времени T :

t >  tT, x >  xL, z >  zL, y >  yL, k, >  kL,

V x > V x L / T , V y > V y L/T , v >v / T.

Тогда, используя обозначение k y для k y L и обозначение V a для безразмерной альфвеновской скорости V a L ^–1 T , мы имеем в качестве исходных по-прежнему уравнения в виде (1), но уже для безразмерных переменных и функций.

Будем полагать, что при t=0 имеет место смещение и ускорение плазмы в направлении, перпенди- кулярном магнитному полю:

v±( t = 0) = Vi(0), d t v±=d t v±(0), где начальные возмущения ν⊥(0) и ∂tv⊥(0) – функции x и z.

Сделаем для возмущенных величин преобразование Фурье по z вида

∞

• ^v ± k = J e ^{- lkz} v ± dz .

  -∞

Обратное преобразование имеет вид

∞

• V ± = ( ^{2 n} ) ^{- 1} J e ik v ± k ^dk .

  -∞

По времени делаем преобразование Лапласа:

• v _± k _m = J e ^{i m} t v ± k dt .

Обратное преобразование дается формулой ∞+ic v±k =(2n) 1 J e-i™tv±kmdto,

-∞+ic где контур интегрирования должен лежать выше всех особенностей подынтегрального выражения.

Умножаем обе части уравнений (1) на e ^{- ikz} e ^{i ω t} и интегрируем от – ∞ до ∞ по z и от 0 до ∞ по t . Обозначив U _l=-!5 t v _± k ( ⁰ ) + i ^to v _L k ( 0 ) и l a =to ² V , ^{-2 - k 2} , получаем из (1)

laVxkm=-5xVk  ■ Ux ,(2)

laVykto=- iky V k to+ Uy ,

ψkω = ∂xvxkω + ikyvykω.(4)

Из этих уравнений следует уравнение на ψ k ω :

dx (l;*d x V k to) + (1-ky l-1 )v k to= F,(5)

где F = d x ( l;*U x ) + zk y l;*U y .

Дивергенция скорости ψ описывает сжимаемую часть возмущения, таким образом, мы имеем уравнение (5) в качестве уравнения для БМЗ-возмущения. Будем для определенности полагать, что альфвенов-ская скорость имеет один минимум при x= 0 и монотонно возрастает как функция I % | , так что V_a >да при I x I >да . Тогда l a > - к ² при I x I >да . В таком случае можно в качестве граничных условий для (5) выбрать убывание возмущения при I x I >да .

Решение уравнения (5) может быть представлено в виде

∞

V k ш = J ^F ( ^ , ^ю ) G ( x , ^ , to ) d ^ ,

-∞ где G(x, ξ, ω) – функция Грина. Она удовлетворяет уравнению dx (/;15 xG (x, ^, to)) + (1 - ky l- )x xG (x, ^, to) = §( x — У и граничным условиям (ГУ) при |x| > да. Мы ука- зываем у F и G в качестве аргументов только те переменные, которые участвуют в последующих преобразованиях с использованием F и G .

Обратное преобразование Лапласа по го дает временную эволюцию БМЗ-возмущения, произво димого vik(0) и dtvik(0). Имеем

• 1    ю+ ic       ю

V k ( x ) = y J e~i ™ t J F ( ^ ’ го ) G ( x , ^ го ) d ^ d ro . (6) ^{2 П} -ю+ ic    -ю

Функция Грина может быть записана в виде

G (x, ^ro) =        1777----7 g (x, ^ro), la (x, ro) W (x, ro)

g ( x , £ , ro ) = V 1 ( x , ro ) v ₂ ( ^ , ro ) 9 ( ^ - x ) + +V₂ ( x , ro )vi ( £ , ro ) 9 ( x -y .

Функции v 1 и V 2 — решения однородного уравнения, соответствующего (5):

5 x ( la^ x V k ro ) + ( 1 - kyla" ) v k ro = 0,               (8)

решение v ₁ удовлетворяет ГУ при x ^ - ю , а решение V 2 удовлетворяет ГУ при x ^ю . W ( V i , V 2 ) в (7) — определитель Вронского для функций Vi и V 2 :

W ( v i , V y ) = V i ^d x V 2 ^- V y ^d x V i ;

произведение

L ^ ( x , ^ro ) W ( x , ^ro )

не зависит от координаты x . Функция 9 в (7) -функция Хэвисайда: 9 =1 при x > 0, 9 =0 при x < 0.

Представление для эволюционирующего МГД-возмущения через решение неоднородного уравнения для преобразования Лапласа этого возмущения с использованием функции Грина применялось, например, в [Tataronis, Grossmann, 1973; Grossmann, Tataronis, 1973]. Исследование выражения вида (6) в [Tataronis, Grossmann, 1973; Grossmann, Tataronis, 1973; Zhu, Kivelson, 1988] позволило определить асимптотическое поведение БМЗ-возмущения при t ^ю при наличии связи БМЗ и альфвеновских волн. Мы хотим сначала получить описание временного поведения БМЗ-возмущения с заданным к во все моменты времени t > 0, а затем, используя уравнение (3), найти также временное поведение альфвеновского возмущения с заданным k . После этого с помощью обратного преобразования Фурье мы получим описание пространственновременной эволюции альфвеновского возмущения.

Для того чтобы с помощью обратного преобразования Лапласа получить описание временного поведения БМЗ-возмущения с заданным k во все моменты времени, мы до его выполнения предварительно преобразуем подынтегральное выражение в (6) – при этом необходимо учесть, что связь БМЗ и альфвеновских волн является слабой, – и перейдем от решений уравнения (5) к решениям соответствующего уравнения нулевого порядка по связи БМЗ и альфвеновских волн.

Волноводные моды без учета связи БМЗ и альфвеновских волн, дисперсионное уравнение, декремент

Мы будем описывать эволюцию возмущения для случая, когда в начальном возмущении являются существенными только малые ky. В этом случае связь БМЗ и альфвеновских волн можно считать слабой, и мы будем далее использовать это обстоятельство. В настоящем разделе мы получим соотношения для нулевого по связи БМЗ и альфвенов-ских волн приближения, которые применим в дальнейшем. Будем обозначать верхним индексом (0) величины в нулевом приближении.

Для дивергенции скорости при ky= 0 имеем из (5) уравнение без учета трансформации в виде dx (la"5 x vS) + vS= F(0),                     (9)

где F ( ^{0 )}=5_;r ( l - U ) . Это уравнение не учитывает связь БМЗ и альфвеновских волн, и, хотя в нем имеется особенность, его решения не имеют особенности, соответствующей резонансу БМЗ и альфвенов-ских волн. В этом легко убедиться, например, с помощью метода Фробениуса. Еще более простой вид ( 0 )

имеет уравнение на v (^^ , через решения которого мы выразим решения (9). Так как при k y = 0 дивергенция скорости определяется только x -компонентой скорости

V k °ro =d x v xk ro ,                                          (10)

то из (9) получаем уравнение для v(°), в виде dx dxvxkro+ lavxk ro= Ux.                                (11)

Граничными условиями для этого уравнения являются условия убывания | v ⁽°)₀| при I x |^ю .

Таким образом, однородное уравнение, соответствующее уравнению (11):

d _x d x v ⁽⁰⁾+ l_av ⁽⁰⁾= 0,                                   (12)

совместно с граничными условиями убывания, является задачей Штурма–Лиувилля на бесконечном интервале.

Обозначим v ^{( 0 )} собственные функции (12), отвечающие собственным значениям Q ^y . Нетрудно убедиться, что задача (12) обладает теми же свойствами, что и задача Штурма–Лиувилля на конечном интервале: собственные функции v ^{( 0 )} , отвечающие различным значениям Q 2 , ортогональны с весом V - ² ; собственные значения Q 2 действительны. Собственные функции могут быть выбраны действительными. Мы будем полагать далее, что v ^{( 0 )} выбраны действительными и нормированы следующим образом:

ю

J V ;² ( ^x ) ^v ^ ⁰⁾( ^x ) ^{v ( O} ( ^x ) ^dx = 5 nm ,                   ⁽¹³⁾

-ю где 5nm - символ Кронекера.

В силу (10) собственные функции v(0) однородного уравнения dx (l-dx V(0)) + V(0)= °                            (14)

( ° )

связаны с v () соотношением

у⁽⁰⁾ = 5 v(⁰¹. т п     x х nr

Обозначим W ( v^{; o |} . V : ⁰ ) ) определитель Вронского для функций v^{( 0 )} , v^J₂ ^{0 |} — решений уравнения (14), удовлетворяющих условиям убывания при x ^ - го и x ^го соответственно. Обозначим W ( v ^{0 )} , v ^{( 0 )} ) определитель Вронского для функций v ^{( 0 )} , v ^{( 0 )} - решений уравнения (12), удовлетворяющих условиям убывания при x ^ - го и x ^го соответственно. Имеем

W ( v 1⁰ ' . V 2^{0 )} ) = v 1^{0 |}5 х V 20 ¹  ^^ d x vY .

^W ( v i ^{( 0 )} . ^v 20 ¹ ) = ’ ^ ^d x v 20 ^{- v} i^⁸x v i ^{( 0 )} •

Так как из (10) и из (10), (14) имеем

w(0| =5 i/0'  / 'c w(01 = —т(0' то

V 1,2    ^d x ^v 1,2 ’ l a ^d х ^V 1.2     4.2 . ^{1о                  (16)}

W ( v^{( 0 )} , v 2^{0 )} ) = l a W ( v ^{( 0 )} . v ) •                      (17)

Функции W ( v ( ⁰ , v v | и l - W ( v^{J 0 |} . V 2 ° ) )

не зави-

сят от x .

Определитель Вронского W (vj0), vj0)) и тождественно равная ему функция l-1W (у^1. V20)) обра щаются в нуль при тех значениях го2, при которых (0)      (0).(0)            (0)    (0)

решения у;1, Т' совпадают c у^). а v 1, v(' сов падают с v(0), т. е. при го2 = 02; таким образом, уравнения W (v, v(°)) = 0 и l-1W (у(0), у(20)) = 0 являются разными формами дисперсионного уравнения нулевого по связи БМЗ и альфвеновских волн приближения. Решения такого дисперсионного уравнения определяют действительные 02 как функции к-2

Уравнение (14) имеет действительные собственные значения го ² = 0 2 потому, что в нем по сравнению с (8) отсутствует член с к 2 , описывающий связь БМЗ и альфвеновских волн. Учитывая этот член в (8) как малую поправку, с помощью стандартной процедуры теории возмущений можно найти мнимые части частот, при которых имеются решения (8) у n , удовлетворяющие граничным условиям убывания при I x | ^го . Дифференцируя обе части (8) по x и используя в первых двух членах обозначение v_n :

vn = - la1^ х V г , получаем д д v + 1 v = —к25 (7-1w V х х n an     ух у a т п )

В этом уравнении правая часть учитывает связь БМЗ и альфвеновских волн. Комплексные частоты, при которых имеются решения (8), удовлетворяющие граничным условиям, записываем в виде

^ГО n ± =±° n — i Y n ,

где для Оn при действительных к выбрано положи- тельное значение. Значение декремента не зависит от знаков к и действительной части гоn; запишем последовательность вычисления уn только для Re гоn=Оn, к>0.

Представляя у _n и v n в виде

V . = l"’ + vY .   |^|i||<<|v"|.

v , = v n ⁴+ v n ".   | v n"|«| v n -'|.

имеем

⁸ х ⁸ х ^ ^{+ l} a ( ° n ) ^v n ^-

-2zQ у   -²v⁽⁰⁾ = -k²d (Z^-1\|/⁽⁰⁾

n « n a n           y х у a I n J

Умножая обе части этого уравнения на v(0) и интегрируя от -го до го, получаем го        ,._..?

2 i О „ Y _и J V;² ( v < °)) dx =

-го го..-

= к2 Im Jv( 'd^l U (02)) у(0) | dx• y     nx  a  nn

-го

Используем условия нормировки (13) и то, что го                        ..-1

J ^vV ⁸ х [ ( ^l a ( ^O n ) ) V n ⁰⁾ ] ^dx =

-го го

= - J ( d x V ⁽ ₁ ⁰⁾ ) ( l„ ( o n ) ) dx .

-го а также полагаем l-1 = ^к^;^ и

^V a = ^V a ( ^хп 1.2 ) ⁺ ( ^d x ^V a ) ( х „, ₂) ( ^х - ^хп 1.2 ) .

где x n 1, 2 – точки, в которых выполняется резонансное условие l _a ( О 2 ) = 0.

В случае, когда альфвеновская скорость имеет один минимум и монотонно возрастает как функция I х I , таких точек две - x_n 1 и x_n 2 . Учитываем, что правило обхода особенности l _a ( О 2 ) = 0 задается тем, что Im го >0; в результате получаем

Y_n=n — 7— Kfd^ v ⁽⁾) (d., V ) / V I +

”     4 к ²О Ю- ^х ” ^{! х} a⁷ a ¹ X )

x i                               in и       (19)

+ f ( d x v г ^o))² 1(5 x V a ) / V a Г* ¹     } •

^                                  ^ ( ^х п 2 1 J

Запишем функцию Грина для уравнения (12). Она нам также понадобится в следующем разделе для использования в (6) малости связи БМЗ и аль-фвеновских волн. Обозначим функцию Грина для уравнения (6) как G^'0* • Она может быть представлена в виде разложения по собственным функциям v(0) • Действительно, если предположить, что решение уравнения д х 5 xG;5+ laGi°)l=8( х-^)

можно представить в виде

G ^{( 0} ) = Уа v⁽⁰ ’

^G ( x )    ^T a n v n ’

n имеем

Tan [[®2-°]]vn°’=5(x-^).

Умножая обе части на v ( ^ и интегрируя с использованием условия нормировки (13), получаем

^G ( x > =E , 2 ’   1 vn“ ( x ) ^V№            (20)

n L®  °n]

Эволюция волноводного  БМЗ-возмущения при слабой связи БМЗ и альфвеновских волн

Описание эволюции начального возмущения при слабой связи БМЗ и альфвеновских волн в настоящей работе основывается на том же методе, который использовался для исследования эволюции в общем случае произвольной связи [Tataronis, Grossmann, 1973; Grossmann, Tataronis, 1973; Zhu, Kivelson, 1988] и который восходит к задаче Ландау о затухании электромагнитных волн в плазме. Ключевым звеном этого метода является аналитическое продолжение функции Грина из области значений го с положительной мнимой частью, для которых осуществлялось преобразование Лапласа, в область го с отрицательной мнимой частью с сохранением правила обхода особенностей, получаемого в верхней полуплоскости. Последующая деформация контура интегрирования по го в обратном преобразовании Лапласа позволяет получить асимптотическое описание эволюции начального возмущения при t ^^ [Ta-taronis, Grossmann, 1973; Grossmann, Tataronis, 1973].

Отличие способа, применяемого в настоящей работе, от классической процедуры исследования интеграла в обратном преобразовании Лапласа состоит в следующем: чтобы получить возможность описания эволюции с начального момента времени, мы до выполнения аналитического продолжения подынтегрального выражения в (6) преобразуем его, используя медленность резонансной трансформации, обусловленную слабой связью БМЗ и альфвеновских волн, а уже затем осуществим аналитическое продолжение.

Запишем Vi 2 в виде

V 1,2 ( x , ®) = V ⁽°2 ( x , ®) + V⁽ 1 ’ 2 ( x , ® ) .

В силу слабости связи БМЗ и альфвеновских волн можно полагать

| V(1 ’t (x, ®)| << |v(02 (x, ®)| ■

Пренебрегая малыми отличиями Vi 2 ( x , ® ) от V ^{( 0}’₂ ( x , ® ) , получаем в (6)

G ( x , ^ ® ) =        ¹ ------- g ⁽⁰⁾ ( x , ^ ® ) ,      (21)

l-W (Vn V2)

где

g(0) (x, £, ®) = V(O) (x, ®)v20) (5,®)9(^-x) + +V20) (x, ®)v(0) (£,®)6(x -^)■

У g(0) нет особенностей, связанных с наличием резонанса, поэтому особенности функции Грина G в виде (21) как функции го обусловлены только знаменателем этого выражения. Функция G имеет полюсы при тех значениях го, при которых знаменатель в (21) равен нулю. Функция l-1W (Vi, V2) не зависит от х; она обращается в нуль при тех значениях го, при которых обращается в нуль вронскиан, т. е. при тех значениях го, при которых решения у,, у2 сов падают c уп, удовлетворяющими граничным условиям на обоих концах. Процедура аналитического продолжения функций Vi, у2 в область значений го с отрицательной мнимой частью с сохранением правила обхода особенностей по го, имеющего место в верхней полуплоскости комплексного го, дает также аналитическое продолжение вронскиана в область значений го с отрицательной мнимой частью. Однако для вычисления нулей вронскиана в случае слабой связи сами функции Vi, V2 не нужны. Мы уже нашли в предыдущем параграфе значения го, при которых имеются решения Vn, удовлетворяющие граничным условиям на обоих концах, тем самым мы определили нули вронскиана. В результате применения теории возмущений мы имеем для нулей формулы (18), (19), содержащие только функции нулевого приближения; при получении (19) использовалось правило обхода, соответствующее аналитическому продолжению Vi, V2 из верхней полуплоскости комплексного го. Нули вронскиана располагаются в области значений го с отрицательной мнимой частью:

® = ®n + = °n - iYn и ® = ®n - = °n - iYn ■

Таким образом, интеграл по ® в обратном преобразовании Лапласа с функцией Грина в виде (21) можно свести замыканиями контуров в нижней полуплоскости при t > 0 и в верхней полуплоскости при t < 0 к суммированию вкладов от полюсов функции Грина (21) при ® = ® _{n +} и ® = ® _n _ .

Перед вычислением интеграла по ® предварительно преобразуем входящий в него интеграл по ^ . Во-первых, полагаем в нем

F = F ⁽⁰⁾ =5 x ( L⁴U_X ) ■

Во-вторых, используем равенства ю                                               1

-[F'•>(?, ®) G (x, . ®) d6 = - i-w^ X xj I- (^, ®) Ux (^, ®)d, g<0) (x, ^, ®) d ^,

-^

5^g<0) (x, ^, ®) = 0(^- x) v10) (x, ®)5^у20) (^, ®) + +0(x-^)v20) (x,®)5^v10) (^,®).

Так как с учетом (16) имеем i-e^ g (0>(х, 5го)=

= —0(5— х > (ах v(0>( х, го> )v 20>(5, го>—

—9(х — 5> (ахv20>(х, го>)v(0> (5, го>, 9(5 — х)v,'0)(х, го)v(0)(5, го) + +9(х — 5)v(0) (х, го)v(■0) (5, го) =

= W ( v ( ^{0 )} , v 2^{0 )} ) G х °)) ( х , 5 , го ) ,

i;‘ (5)d5g(0> (х, 5, го) =

= — W ( v ( ⁰ ) , v 2^{0 )} ) д х б ( 3( х , 5 , го ) .

Обозначение G ( 0 ) введено выше для функции Грина уравнения (12). Так как W ( v (( ^{0 )} ( 5 ) , v ( ^{0 )} ( 5 ) ) не зависит от 5 , то мы заменили W ( v (( ^{0 )} ( 5 ) , v ( ° ) ( 5 ) ) на W ( v (( ^{0 )} ( х ) , v ( ^{0 )} ( х ) ) .

С учетом (20) получаем

IJ1 (5)^5g<0> (х, 5, го) = —W(v(0), v20))х

^X Z z 2 '^Х ( ^д х ^V2⁰ ^ ^х , ^{к 2} )) ^v , ⁽, ^.

• 2    (го -Q„)х

  
  

Таким образом, подставляя (23) в правую часть (22) и учитывая (17), (15), получаем в (6) вместо

JF (5, го, к ) G ( х, 5, го) d5

-го выражение

w^vvV0))

W(vi, v2) n(го2-q2)

V 2 ⁰⁾ ( х )

го

х/их (5, го)рП0>«)d5.

-го

Обратное преобразование Лапласа (6) принимает вид

V к = ~Х

2п го

J e -

-го го

W ^vT,^^ ^W ( V 1 , V 2 ) ² ( го ² -Q 2 )

V 2 °* ( х ) x

xJUx (5, го)v(0) (5)d5dго. -го

Замыкая контур в нижней полуплоскости при t > 0 и в верхней полуплоскости при t <0, можем заменить интегрирование суммированием вкладов от

При го ² — Q 2 = 0 особенности нет, так как

W(0)(v(0), V(0)) = 0

при го2—Q = 0.

вычетов.

Так как можно полагать dW (V1, V 2 ) d го2

- ( ^{го 2} ± )

dW ( v ( ^{0 )} , V"j

d го ²

^{( q 2} )

то вблизи полюсов

^W ( v⁽ °) , V 2^{0 )} )/ ^w ( V ' , V 2 ) ^x

x' (го2-Q2 ) = ' (го2-го2 ±);

для знаменателя имеем

( ^{го 2} — ^{го 2} ) = ^{2 го} 2 ± ^{( го} — ^го 2 ± ) = ^{± 2 Q} 2 ^{( го} — ^го 2 ± ) .

Также следует положить и х ( 5 , го 2 ± ) = и х ( 5 , ±Q 2 ) .

Получаем

V к =9( t )Z(v kn+e "im2+‘ +V kn - e "1го 2—t), где

vkn± = cn± (k2) v20) (х, k2),                       (24)

1 го

Cn±(к2 ) = т — ^ux (5,±Qn, к2) v20)(5,к2)d5.

Поскольку в дальнейшем v^± будут использоваться в обратном преобразовании Фурье по к, то мы выписали в выражениях для них аргумент k2, который опускали ранее. С учетом определения Ux имеем го

cn± =2/1 vA (0)± i7Г5-vхk (0) I v2 (5, к )d5 —го V                             /

Мы получили, что в случае слабой связи БМЗ и альфвеновских волн фурье-образ БМЗ-возмущения с начального момента времени представляет собой суперпозицию мод, которые можно назвать коллективными модами главного приближения при малой связи БМЗ и альфвеновских волн. Структура этих коллективных мод по координате вдоль неоднородности определяется функциями v ⁽⁰> , т. е. такая же, как у мод нулевого приближения, в котором связью БМЗ и альфвеновских волн пренебрегается, но их комплексные частоты содержат декременты, отражающие трансформацию коллективных мод в аль-фвеновские волны.

Эволюция альфвеновского возмущения при начальном возмущении в волноводе

Альфвеновское возмущение является несжимаемым, компоненты возмущения скорости в нем v(a>, v(a> связаны уравнением dxv(a> = -ikyv(a>, поэтому достаточно найти v(a>. Воспользуемся для этого уравнением (3). Нас интересует альфвеновское возмущение, образующееся в результате трансформации БМЗ -возмущения в волноводе, а не альфве-новское возмущение, вызываемое непосредственно начальным возмущением. Поэтому мы предполага- ем, что в области, где происходит трансформация, начального возмущения нет, и полагаем Uy = 0. Так как y-компоненту скорости мы вычисляем только для альфвеновского возмущения, то индекс (a) писать далее не будем. Для сокращения записи мы будем далее рассматривать альфвеновское возмущение, производимое пакетом коллективных мод с одним номером n; будем отмечать такое возмущение нижним индексом n. Сначала найдем альфвеновское возмущение в k-представлении. Из (3) имеем:

ykmn vyk to n       i^y la

Обратное преобразование Лапласа для v дает

__   21    1     (   -itot ykton v.n = -iky;;- I e   —;d

2 n

—x+ica

Записывая yton в виде to

Уkton = p ' (уkpn+e"*”n+t + Уkpn-e-"n-t)dт и сводя интеграл по to замыканием в нижней полуплоскости при (t-т)>0 и в верхней при (t-x)<0 к суммированию вкладов от полюсов, получаем при t > 0

V vykn = iky^ I У kn± Х

------¹------- Г e -^{i to} " ± t - e V a

L kVa -to n ± ^L

+1      Г e - i™n± t — eikV,t kVa + to n ±L

где I означает суммирование выражений с верхним и ± нижним знаками.

Альфвеновское возмущение v_ykn состоит из вынужденных и собственных колебаний:

v ykn = ik y V - iv kn ±

2 k ±

. ^kV a ^-to n ±    ^kV a ^+to n ±.

^V E = ^{- ik} y V- 1У kn ± ^Х

2 k ±

_Х       ¹ e -i^kV a ‘ ₊      ¹ e V

_ kV , ^- Ю „ ±         kV_fl + Ю _n ±

При y n t ^1 вынужденные альфвеновские колебания v ⁽2 затухают и остаются только незатухающие собственные альфвеновские v ⁽ E ¹ .

Мы видим, что vykn как функция k имеет полюсы, положение которых на плоскости комплексного k определяется уравнениями kV- =ton ± (26)

kV_a =-to n ± .                                    (27)

Обозначим решения (26) kn±, где kn± - функции одной переменной x. Их действительные части сов- падают по знаку с действительной частью частоты, которой они соответствуют, и, значит, возмущения с такими k имеют положительную фазовую скорость и распространяются в направлении z=^_ Решениями (27) являются k=-kn±, действительные части которых противоположны по знаку действительной части частоты, следовательно, возмущения с таким k имеют отрицательную фазовую скорость и распространяются в направлении z=-^.

Обозначим K 2 значение k2, которое является корнем уравнения on (k2)- k2V2 (x) = 0.                        (28)

Мы положили для простоты, что такой корень только один. Выбираем K n > 0. Ясно, что K n является функцией одной переменной x . Эта функция (назовем ее резонансное волновое число) дает модуль волнового числа, при котором БМЗ-волна, квадрат частоты которой равен 0 2 ( k ² ) , будет в резонансе с альфвеновской волной, квадрат волнового числа которой равен k ². Запишем решения (26) в виде k n ± = ± K n . Запишем to _n ± ( k n ± ) в виде разложения вблизи k = ± K n :

^to n ± ( k n ± ) = ± ^o na ^- ±--- n- ^^-)" | k =± K n i ^Л n ^- i ^Г n .

Мы обозначили О na =О n ( к - ) и Г n =Y n ( к - ) • Согласно (19)

^Г • =’ 4s; ^d - V . ) 2 ( - ^V . ) / V - Г' )„_/

+ (( ^d .V. ) ²1( 5 -^v. )/ v , Г' 1. J.

⁽ X n 2 ) )

где X_{n 1, 2} – точки, в которых выполняется резонансное условие l _a ( 0 2 ) = 0. Таким образом, декремент Г _n является функцией только x . Он описывает затухание коллективных мод, модуль волнового числа которых равен K_n , вследствие их трансформации в альфвеновские волны на поверхностях (точнее, с учетом коллективного характера мод, вблизи поверхностей), где альфвеновская скорость имеет значение V a ( x ).

Обозначим V gn групповую скорость при k = K n :

dsn-    = v dk lk=к-     gn

Ясно, что V gn равна модулю групповой скорости резонансных мод. О _n как функции k ² определяются из уравнения

W ( v-°? . v< °2> ) = 0.

где W является функцией to ² и k ² (не зависит от x ), так что можно записать W ( to ², k ²) = 0.

Дифференцируя это равенство по k, получаем dto_ k dW , dW dk     to dk2 d to2

отсюда

0^ I „ =-V dk    Kn      gn

Таким образом, гоn±(kn±) = ±Qna -YnЛn -iГn.

Подстановка го_п± ( k_{n ±} ) в таком виде в (26) дает

Л n =Г n / ( V a - V gn ) .

Мы получили, что на поверхности с координатой x в резонансе с альфвеновскими волнами находится набор коллективных мод, у которого спектр значений к имеет ширину Л _п , малую в силу малости Г _п .

Таким образом, наличие функций (kVa - го п ± ) -1 и (kVа+гоп±)-1 приводит к тому, что в возмущении, создаваемом пакетом коллективных мод с номером n, существенен только вклад мод с такими действительными к, что |k ± КД Л^п • Поэтому можно использовать вместо гоп± их разложения вблизи к=Kn и к=-Кп или эквивалентные им в силу малости Лп разложения вблизи кп± и -kn±. Поскольку при к, близких kn±, гоn± = kn±Va + Vgn (k - kn±),

и

vУ ykn

где

, ( I )( - ) ykn

+ v⁽ E ^l(-)

ykn

ik V

_v ⁽ I )B =_____________ ykn     2 k ( V_a - V_g „ )

^X ^V kn ±

±

X

¹        _e- i ( k n ± V a - V gn ( k + k n ± ) ) 1

( ^{k + k} n ± )

у⁽ E ⁾(^-) =__ ^ikyV a _____у      _____¹_____ ik V„l

"■        2 k ( V , - V, ).^V k" ± ( k + k . , )      .

Индексами ( I ) и ( E ), как и выше, отмечены вынужденные и собственные колебания соответственно.

Для получение формулы, описывающей продольную структуру возмущения, следует сделать обратное преобразование Фурье функции v_ykn по k . Вычислим обратное преобразование Фурье сначала для v ykn ^{( I )(+)}. Получаем

V(I)(+) =____ikyV,____у да ik^-c ш<°> (x k 11X vn     4n(V - V I'tJ    n±vn (x’k )X

' ^{a gn}* ^-да                                 (29)

X

и при к, близких -кп±, гоn± = kn±Va - Vgn (k + kn±),

то с использованием этих разложений получаем вместо (25)

ikyVa v 1  =---------?Х yn 2к (V - Vgn)

^X SV n„ ±

±

exp ( ^- i ( k„ _± V + V gn ( к ^- k„ _± ) ) t ) ^- exp ( ^- iki'i ) ( ^{k - k} n ± )                  ⁺

( ^{k + k} n ± )

(^ i ( k n ± ^V a ^V gn ^{( k + k} n ± ) ) ¹    ^ikV a t

) .

Действительная часть k выделяет резонансные значения к (| k | = K_n ), а мнимая часть задает ширину резонанса Л _п по продольным волновым числам.

Возмущение v_ykn состоит из волн v ^, v У, распространяющихся в направлениях z = да и z =- да соответственно. Имеем

V ⁽+) = V , ykn     ykn

( I )( + ).,,    ( E )( + )

⁺ v ykn      ,

где

V_ta ⁽ I ^)Н ykn

ikyVa

^{2 k} ( V - V gn )^Х

^X ^V kn ±

±

^ex P ( - i ( ^k n ± V , + V gn ( ^{k - k} n ± ) ) t ) ( ^k - ^k n ± )

( E )( + )₌_     ik y V a    _y     2 exp ( - ikV , t )

yn    = ^- 2 k ( V , - V gn )^ kn ±    ( k - k n ± )   ;

¹ ^[^{- ik} n ± ^V a ^{- iV} gn ^{( k - k} n ± ) ] ^{1 k} ( ^{k - k} n ± )

dk .

Мы вернулись в (29) к записи ^^± в виде (24).

Запишем д _tv_xk (0) и у_хк (0) в виде интегралов, которые дают преобразование Фурье функций d_z v_x ( 0 ) и v xk (0) по продольной координате:

оо

V xk ( 1 = 0 ) = J e - ikl v, ( 0 ) dl

-да

и oo д .vxk (0 )= J e ",kl д zvx (0) dl.

-да

Подставляя эти интегралы в c , имеем oo cn ± = J e" ,klcn ± dl,

-да где

(да                            A cn±=2 Jvx(0)±ikNд-vx(0) vn^ k )d^. \-да                             /

Вследствие наличия в правой части начальных возмущений д t v x (0) и v x (0), функции c зависят от продольной координаты l, а наличие Q _п и v ^{( 0} ) приводит к зависимости c от k ², так что c – функции l и k ².

Используя c , вместо (29) получим

v ( I )( + ) yn

ik y V a

4 V a - V gn )^X

V (+W ¹ ) ^{(+ )}_+V( E )( + ) yn      yn        yn

,

X

то TO

Z JJ e i ⁽ z — l ) C n ± dl V n ^o) ( x , k ²)

- -TO-TO

x e [-*„ ± V     ^{( k -} kⁿ _±) J t 1 dk .

k ( k — kn ±)

X

Для выполнения интегрирования по к используем то обстоятельство, что подынтегральное выражение имеет полюсы при к= k n ± . Так как k n ± = ± K_n - i Л _n , Л _n > 0, то полюсы находятся в нижней части комплексной плоскости. При ( z - l - V gn t ) < 0 замкнем контур интегрирования по к снизу с охватом полюсов, при ( z - l - V_gnt ) < 0 замкнем контур интегрирования в верхней полуплоскости, где полюсов нет. Как в том, так и в другом случае интеграл по замыкающей части контура стремится к нулю в силу того, что e ik e i ^kl e ^ gn ⁽ ” ^ ^ 0 при | к I ^то , поэтому интеграл от - то до то равен интегралу по замкнутому контуру. Таким образом, интеграл по к сводится к суммированию вкладов от вычетов. Функции v (0) , v ⁽ 0 ) - функции к ² и x . В полюсах при к = к_п ± в силу малости мнимой части к_п ± можно полагать О ( к 2_± ) = О_а, а также

(0)         2          (0)          2

V n (x, kn± ) = V n (x, Kn ) , (0)(x £2       0)/y ^2\ vn (x, kn± )   vn (x, Kn ) •

Поскольку K² - функция x , то v ⁽⁰⁾ ( x , K 2 ) и

v ⁽⁰⁾ ( x , K² ) - функции только x . Обозначим их v„ и V n соответственно; они описывают структуру по координате x возмущений дивергенции скорости и x -компоненты скорости в резонансных модах.

Обозначим также е_п± при к² = K² как Cn ± . Имеем

1 ТО                                           1

C n ± = 2 J V x ( ⁰ ) V n ( 5 ) ^d 5± i ^X

—то                              naa то xjdv (0)Vn (5)d5.

-то

Таким образом, для v ⁽ I ⁾⁽⁺⁾ получаем

V a

v(I)(+) = к 1 V ____________ yn       y 2K   n n V a gn )

X

. j    ₍ e in + ^{( z —} l ^— V a t )_j|+— e^k„ — ⁽ z ^— l ^— V a t ),,_ ) dl.

^{( z —} V gn t )

Аналогично для собственных колебаний получаем

V a

v(E)(+)=— k __1__V __________ yn         y 2K   n n         a     gn

X

. то    ₍ e^ + ^{( z — 1 —} V a t )    — ₍, k — ^{( z — l} — V a t )_B_) dl .

( z — V a t)

Поскольку V_gn < V a , все возмущение

распространяющееся в направлении z = то , описывается формулой

( + )         i ²

v2”^=— кУ 2FVn

V a ( ^V a — V gn )

X

^{( z} V gn t )

^: J ( e

( z — V a t )

,^ik n + ^{( z} l  V a t )

n +

_— e i” — ( z — ¹ — V a t )

) dl.

Поставляя C n ₊ и C n _- из (30), получаем

v(+) = — i yn

k y      V a

2K n    a     gn

V n ^X

(z Vgnt)

X J  eAn (z—1—Va<)| _C” 2 ( sin ( K” (z — l — Vat)))+

( z—Vat)

⁺ TT ^C ” 2 ( cos ( ^K ” ( z ^{— l —} V a t ) ) ) I ^dl ,

^na7

где

то

C n 2 = J d t v x ( 0 ) V n ( 5 ) d 5 ,

-то то

C n 1 = J v x ( 0 ) V n ( 5 ) d 5 .

-то

Коэффициенты С_п 1 и С_{п 2} представляют собой коэффициенты разложения начального возмущения по собственным функциям V ; они являются функциями z . Таким образом, пакет (32) состоит из двух составляющих: одна обусловлена наличием в начальный момент времени начального сдвига плазмы со скоростью v x (0), а другая - наличием ускорения d _tv_x (0), которое получает плазма при этом сдвиге.

Формула (32) описывает весь процесс возникновения, нарастания и распространения альфвеновско-го возмущения. При t = 0 альфвеновское возмущение отсутствует, его нарастание происходит, когда с увеличением t увеличивается интервал интегрирования. Множитель e ^{Л n ( z —} l ^— V^at ) , убывающий при возрастании переменной интегрирования от ее нижнего предела, ограничивает область интегрирования, дающую существенный вклад в интеграл. В результате при Л _n ( V_a — V_gn ) t >1, т. е. при Г _nt >1, верхний предел интегрирования в (32) можно заменить на то , и мы получаем (31), т. е. только собственные колебания. Таким образом, формула (31) описывает аль-фвеновское возмущение после затухания породившего его волноводного возмущения.

Применим (32) для исследования зависимости пространственно-временной структуры альфвенов-ского пакета от соотношения масштабов начального возмущения и резонансных масштабов, т. е. продольных масштабов, задаваемых условиями резонанса. Резонансных масштабов два. Один задается резонансным волновым числом K n . Это длина волны коллективных мод, резонансно поглощающихся на

данной поверхности, Х_п ~ K_п 1 . Другой задается шириной спектра по к этих мод, он есть ~ Л^{- 1} .

Рассмотрим начальные возмущения с различными соотношениями их масштабов и резонансных масштабов.

Альфвеновское возмущение от начального возмущения большого продольного масштаба

Рассмотрим случай, когда начальное возмущение как функция продольной координаты представляет собой гармонику с волновым числом k ₀ и с огибающей большого продольного масштаба, так что C_{n 1} и C_{n 2} можно представить в виде

X cos ф₀ -

-

-Л n

Л,

+2 [(Ik0I - Kn ) +Лn   (|k0I + Kn ) +Лn _

sin Ф 0 ;

^C n 1 = cos ( k 0 z ) A n 1 1 У ,

( Z - Z 0 )

S n

2 = -7--1----\CXP (-Г,1 )X

2 ( Va - Vgn )

-Лn COs (Ф0 + фn ) + (|k0 I - Kn ) sin (Ф0 + Фn )

: V              (Iкcl -Kn )2 +Л2

-Л„COS(фo-ф-) + (|ko|+K-)sin(фo-ф-)

C n 2 = c ^0S ( k 0 z ) A n 2   У, ^{( Z} „ ^{Z 0} )

V       S n

,

2 ( Va - Vgn )

Л2 +(|кa| + Kn )2               j

Лn COs Ф0 - (|k0I - Kn ) sin Ф0

V

(I k 0I - K n ) ² +Л 2

где S_n >Л_и< Если начальное возмущение представляется в виде произведения двух функций, каждая из которых зависит только от одной из координат x и z , то масштаб S n будет одним при всех n .

Множитель e ^{Л 2 (} z ^- l - V a t ) в подынтегральном выражении убывает при возрастании переменной инте-

Лn cos Ф0 - ( к0 + Kn) sin Ф0 +

(I k( J+Kn) +Л 2      j

Мы обозначили

.

грирования от ее нижнего предела, вследствие чего размер области интегрирования, дающий существенный вклад в интеграл, ограничивается размером порядка Л - ¹ . Поскольку 8_п ^> Л - ¹ , то изменением An 1 , An 2 на масштабе области интегрирования можно пренебречь и положить под интегралом

41, 2 I У ,

Sn   j

= A n 1, 2

г y,

V

^{( Z -} V a t ^{- Z} 0 )

Тогда получаем

v(+) = —i V w yn            a T ,

kK

n kr;  ^X

2 Kn ( x )

( ^{Z -} V a t ^{- Z} 0

S n

V

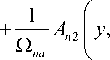
(Z - Vat - Z0 ) '

Sn     j

I ₂

где

I_x =   —¹----; exp ( -Г. ¹ ) x

² ( V a - ^V gn ) ^V     ’

<,,.,__,

(- k0 + Kn )cos(Ф0 + фn )-Лn sin(Ф0 +Фn )

X -----------4-----------------;--+

I               ((| k ,1 - Kn)‘ + Л 2)

^

+ (|кg|+ Kn ) COS (фе - фn ) + Лn sin (Фе - фn )

—

- |kJ + K

j

I ka| + Kn

Iкd|(Z - Vat) = Ф0,Kn (Vgn - Va)t = Фn•

Формулы для I ₁ и I ₂ описывают процесс возникновения и нарастания альфвеновских волн в пакете следующим образом: при t =0 функции I ₁ и I ₂ равны нулю, так как вынужденные колебания (члены с множителем exp(–Г _nt )) и собственные колебания (члены без этого множителя) компенсируют друг друга; затухание вынужденных колебаний приводит к нарастанию суммарного возмущения; при Г_и t > 1 вынужденные колебания становятся малы и остаются только собственные колебания.

Область локализации альфвеновских волн по продольной координате задается A n 1 и A n 2 в (33). Поскольку они являются функциями продольной координаты и времени только через ( z – V_at ), то A_{n 1} и A_{n 2} описывают распространение пакета альфвенов-ских волн с локальной альфвеновской скоростью. Кроме того, как видим из (33), структура огибающей альфвеновского пакета по продольной координате определяется структурой огибающей начального возмущения, так что огибающая пакета имеет продольный масштаб S_n . Если начальное возмущение представляет собой гармоническое возмущение с k = k 0 без огибающей, т. е. A n 1, 2 не зависят от z , то альфвеновские волны, распространяющиеся в противоположных направлениях, складываются в стоячую по продольной координате волну.

Из выражений для I ₁ и I ₂ видим также, что возмущение локализовано по координате x вблизи поверхности, где I к 0 I = K n . Используя неравенство

<<                 ,

(I к 0| - K n ) ’ + Л 2      (| к „I + K , ) ’ + л 2

можно переписать I ₁ и I ₂ в виде

2(V - V-)[(lк.1 -Kn)2 +Л2 +(|к I + Kn)

i2+Л 2

X

11 = 1 (ф0, Ф 2 ) , 12 = 1 |ф0 -П , Ф 2 -П

I = exp (-Г nt )X

x (- \kо| + Kn ) cos (фо + Ф n )-Л n sin (фо + Ф n )

2(Va -Vgn)((|ko|-Kn)2 +Л2)       J

(I ^k ol ^- K n ) cos Ф о ^{+ Л} n sin Ф о

+

2(Va -Vgn)((|kol-Kn) +Л2)

На поверхности x = x_n выполняется равенство I k ₀ 1 = K_n и I принимает значения

I = ^ (-eXP (-Г n ((xn ))t) sin (фо +Ф n ) + sin фо ) . 2Гп

Вблизи x_n имеем K_n ( x )= I k ₀ 1 + K_n ( x_n )( x - x_n ), так что слой, в котором локализуется альфвеновское возмущение, имеет ширину Д_п ~ Л_п ( x_n ) / K ( x_n )| .

Альфвеновское возмущение от начального возмущения малого продольного масштаба

Рассмотрим сначала случай, когда начальное возмущение имеет место только на поверхности z = z ₀. Полагая

C n1 = ^а 2 1 ^s ( z ^{- Z} 0 ) , ^C n 2 = ^а n 2 ^S ( z - ^z o ) , из (32) получаем

(+)     7    1            V

V' 7 = -ik ----ш -----a---- X yn       y 2 Kn  n (Va - Vgn )

xeЛ n(z - z° - Va.)0(-( z - z о - V ))0(( z - z о - Vgnt ))X (-a n 1 ( sin ( Kn ( z - z о - Vat))) +

⁺ 1Г ^a n 2 ( cos ( K n ( z - z о - ^V a ^t ) ) ) I .

^na                           /

Возникновение альфвеновского возмущения и расширение занятой им области по продольной координате описывается произведением 6 -функций. Произведение 6 -функций также описывает перемещение переднего края альфвеновского пакета (обозначим его координату z ₁) по продольной координате с альфвеновской скоростью z 1 = z ₀+ V a t . Как видим, возмущение возникает на поверхности z = z ₀, оно сразу (при t =0) имеет конечную амплитуду на поверхности z=z 1 и дальнейшая потеря энергии волноводным возмущением не приводит к ее увеличению. Однако происходит увеличение размера L альфвеновского пакета по продольной координате: он увеличивается со временем от 0 до L =( V a - V_gn ) t . При Л„ ( V - Vg „ ) t > 1, т. е. при Г_л t >  1, после затухания резонансных коллективных мод увеличение продольного размера пакета прекращается. Таким образом, максимальный продольный масштаб пакета L max - Л _n , а форма огибающей как функции продольной координаты при Г_и t > 1 % может быть описана множителем

6 ( - ( z - z ₀ - V_Qt ) ) e ^Л n ^{( z - z о} - V a * ) .

Теперь рассмотрим случай начального возмущения, локализованного по продольной координате на малом, но конечном масштабе s:

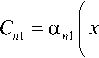
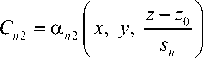
Если начальное возмущение представляется в виде произведения функции x на функцию z , то s _n = s .

Будем полагать, что функции a _d x , у , -—z— ,

V         S n )

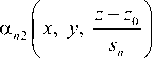
имеют по продольной координате масштаб sn в том смысле, что их можно считать рав- ными нулю при

^{z - z} о s_n

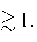
Предположим, что масштаб sn много меньше резонансной длины волны: Knsn ^ 1. Тогда можно пола гать в интегралах все функции, кроме an1,2, равными их значениям при l=z0. Таким образом получаем

у ⁽⁺⁾ = - ik V yn         y a

^n e ^Л n ^{( z z} о ^V a ^t )

2 Kn ( Va - Vgn )

XI cos (Kn (z - zо - Vat)) -1- an2 +

V                     ^ na

+ -sinKn (z - zо - Vat)an 1 ),

X

где a _{n 2}

( ^{z V} gn ^t )                         ^{( z V} gn ^t )

J a n 2 dl ,   ^a n 1 = J ^a n 1 dl .

( ^{z -} V a ^t )                         ( ^{z -} V a ^t )

Поскольку можно считать

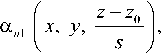
^ 1, то

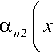
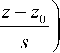
равными нулю при

( ^{z V} gn ^t )

J   a _n 1, ₂ dl = о

( ^z - V a ^t )

при ^{z - z} o    ^V a ^{t +} s n s ^{и z} - ^z о ^Vg^ t - s n .

После затухания вынужденных колебаний при Глt > 1 имеем да                                                  да a n 2 = J a n 2 ( z - zо ) dl, a n1 = J a n1dl.

( ^{z -} V a t )                                      ( ^{z -} V a t )

да

Интегралы J а_{л1 2} dl на интервале z \z - V_at\^s_n ( ^{z - V} a ^t )

изменяют свои значения от нуля до некоторых предельных значений, которые они имеют при z < V a t — s n . Таким образом, за счет наличия этих интегралов в (34) передний край пакета имеет ширину - s _n и его структура дается а_{п t}, а_{п 2}.

Если масштаб sn является малым (sn ^СЛ-1), но больше или порядка продольной длины волны Ks 1 , то в интегралах (32) можно полагать равными своим значениям при l=z0 только экспоненты. Получаем

v(+) = —ik —-— ш yn      y 2 Kn T n

^V a       e ^Л n ⁽ z ^— z 0 ^— V a t ) _X

(Va — Vgn )

X

I “c + сЪ “^ I sin (Kn ( z

\\      ^na    У

—

z ₀

—

—

«У — 1Г “c I cos (Kn (z — z0 — Vat))

⁴¹ na      У                               У

где

( z z 0 V gn t )

0-^,2 = J        cos ( K n n ) d n ,

⁽ z ^— z 0 ^— V a t ) n 1, 2

( z ^— z 0 ^— V gn t )

«^ 2 = J       sin ( K n П ) d П ,

⁽ z ^— z 0 ^— V a t ) n 1, 2

а n = l — z ₀.

После затухания вынужденных колебаний при

Г_й t > 1 имеем

да ac 2 = J cos (KnП) a"1, 2 (x, У, П) dП, ( z—z 0 — Vat )

да

«У 2 = J    ^sin ( K n n ) ^a n i, 2 ( x , У , n ) d n -

( z ^— z 0 ^— V a t )

Функции a⁽ C ) ₂ , O i ) ₂ определяют структуру переднего края альфвеновского пакета. Как и в предыдущем случае, передний край имеет масштаб начального возмущения s_n .

В заключение заметим, что мы полагали резонансное уравнение (28) имеющим только одно решение. Из вышеизложенного ясно, что полученные выше решения (как (32), так и следствия из него) отвечают одному корню, не обязательно единственному. В случае если их несколько, решения, соответствующие различным корням, должны суммироваться.

Заключение