Алгебраическое описание схем алгоритмов программ на основе теории множеств

Для обеспечения однозначности и доказуемости равносильных преобразований алгоритмы должны быть представлены в алгебраической форме (в виде формулы или матрицы) и содержать информацию об операторах алгоритма и связях между ними.

Существующие схемы алгоритмов — граф-схемы (ГСА), логические (ЯСА), матричные (MCA) — не являются алгебраическими описаниями. В частности, ЛСА есть последовательность операторов, не являющаяся уравнением, a MCA представляет собой известную из теории графов матрицу смежности, описывающую только множество дуг ГСА, соответствующих условным и безусловным переходам. То есть в MCA содержатся только переходы алго-ПМТМ9 иг АТА Ч7ТГ‘ТН7\7ТЛ'Г А^Л Ч T-t Я UP ITLf УГ ЛПРПЯТЛПЛП ~                                    *--------,------ что затрудняет математическое преобразование ■ алгоритма в форме MCA. Поэтому, необходимо отыскать способ алгебраического описания алгоритмов программ, который бы позволял: 1) описывать алгоритмы программ любой сложности в виде формулы, и 2) выполнять равносильные

АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ СХЕМ АЛГОРИТМОВ ПРОГРАММ НА ОСНОВЕ ТЕОРИИ МНОЖЕСТВ

При отыскании такого способа необходимо опираться на основополагающие математические дисциплины, каковыми являются теория множеств [1; 7] или конструктивизм [4, 5]. Так как конструктивное направление само построено на уточненном понятии алгоритма (нормальном алгоритме), остается только теория множеств, где одно из ведущих мест занимает понятие «соответствие», через которое, в частности, определяется понятия функции.

Представлению алгебраического способа описания алгоритмов, разработанного под руководством доктора технических наук професора Г. Н. Чижухина и основанного на понятии соответствия из теории множеств и посвящена настоящая статья.

Нами введена основанная на понятии соответствия новая схема алгоритма, названная схемой соответствий алгоритма (ССА), которая в более ранних работах $3; 8; 9] называлась нами инверсной граф-схемой алгоритма.

Схемой соответствий алгоритма называется ориентированный Г = (М,А^ граф, где N' = (1, 2,п ) с N — некоторое подмножество множества натуральных чисел N, образующее множество вершин ССА; А — множество дуг ССА, каждый элемент которого обозначает линейный или условный оператор программы.

Согласно теории множеств [2], соответствие — это тройка, включающая:

• I)    область отправления соответствия. Обозначим ее переменной I,

• 2)    область прибытия соответствия, определяемую переменной /.

■                           © О. В. Кулагин, 2007

• 3)    график преобразования, обозначенный переменной а.

При этом для ССА переменная / есть номер (из множества натуральных чисел) той вершины, из которой дуга исходит, а переменная j - аналогичный номер, но той вершины, в которую дуга входит.

Существует несложный способ перехода ГСА—>, заключающийся в следующем:

• 1.    Каждой дуге ГСА ставится в соответствие вершина ССА.

• 2.    Каждому линейному оператору ГСА ставится в соответствие дуга ССА, обозначение которой совпадает с обозначением этого оператора.

• 3.    Две дуги условных конструкций ГСА переносятся в ССА как две дуги, исходящие из одной вершины предыдущего оператора ГСА.

• 4,    Объединяющимся дугам (циклические и условные конструкции), ставится в соответствие одна вершина ССА (см. вершину 4 на рис. 1, а).

• 5.    Вершины ССА нумеруются натуральными числами (начиная с 1), означающими последовательность прохождения процесса в алгоритме.

На рис. 1 приведен пример перехода от ГСА (рис. 1, а) к ССА (рис. 1, б). На рис. 1, а при помощи кружков с цифрами, соединенных с пунктирными стрелками, показано соответствие дуг ГСА вершинам ССА.

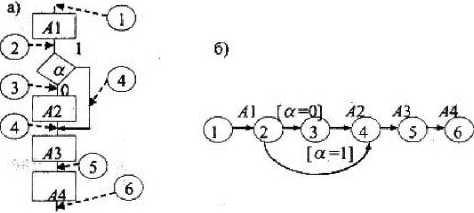
Рисунок. /

Пример перехода от ГСА к ССА: а) ГСА; 6) ССА.

Для описания ССА достаточно указать множество ее дуг, каждая из которых совместно со смежными ей вершинами образует соответствие, которое может быть описано индексными объектами (ИО).

Соответствие, являющееся элементом ССА, может быть представлено в виде индексного объекта, у которого график преобразования а расположен на основном уровне, область отправления I — на нижнем индексном уровне, а область прибытия j — на верхнем индексном уровне. Такой индексный объект нами назван индексным объектом-соответствием (ИОС):

а/ (1)

Всю ССА можно описать с помощью последовательности ИОС. Два ИОС, соответствующие смежным дугам, связанным с разными вершинами, будут иметь одинаковые индексы п, например а- и П_п . При этом первым в последовательности ИОС (в ПИОС) должен находиться ИОС, у которого индекс п находится вверху (область прибытия соответствия), а затем -ИОС, у которого этот индекс находится внизу (область отправления соответствия). Расположенные подобным образом одинаковые индексы п смежных дуг двух ИОС назовем немыми по аналогии с алгеброй индексных объектов [6].

В теории множеств рассматривается только одна операция над — композиция двух соответствий, для обозначения которой используется знак ° [2, 10]. Используя введенное нами обозначение ИОС (1), эту операцию можно записать в следующем виде:

л т ,т

• а, о а„ - Ь_; (2)

При этом количество немых индексов всегда равно двум и порядок расположения их важен: первым всегда должен находиться верхний индекс, при этом композиция по индексам всегда идет слева направо сверху вниз.

Операция композиции двух соответствий применительно к ССА будет означать ликвидацию рассмотрения двух ИОС, соответствующих смежным дугам, и заменой их новым ИОС, график преобразования которого b есть композиция двух исходных графиков преобразования.

Если в выражении (2) заменить т на I, результатом такой композиции будет соответствие, у которого область отправления совпадает с областью прибытия. Такое соответствие описывает циклические конструкции алгоритмов, тогда как выражение (2) — последовательность двух операторов. Поэтому композиция двух соответствий, результатом которой будет являться ИОС с одинаковыми верхними и нижними индексами, названа нами операцией итерации. Для ее обозначения использован знак ромба, и по аналогии с выражением (2) она может быть записана в следующем виде:

4^=^- ®

С точки зрения теории множеств итерация двух соответствий может быть определена как частный случай композиции двух соответствий, когда область прибытия второго соответствия совпадает с областью отправления первого соответствия. В ССА операция итерации будет соответствовать циклическим конструкциям в ней.

График преобразования любого соответствия (1) определяется как некоторое подмножество декартова произведения / х ЛГ В свою очередь, декартово произведение Iх N. само является множеством, из которого можно выделять .разные подмножества, например а" и а” Для этих подмножеств, как и для любых других множеств, справедлива операция объединения (называемая также сложением). На основании этого нами введена операция сложения двух ИОС, имеющих одинаковые нижние и одинаковые верхние индексы:

Операция сложения описывает различные ветвления в программе имеющие одно начало и один конец. Смысл операции сложения ИОС заключается в том, что она означает рассмотрение единой дуги ССА вместо двух параллельных дуг, исходящих из общей вершины и приходящих также в общую вершину.

Для множеств дуг исходной ССА условимся графики преобразований ИОС (переменные на основном уровне) обозначать буквами а. На основном уровне ИОС, который получен в результате выполнения операции композиции (или сложения) двух исходных ИОС, будем размещать следующую маленькую букву латинского алфавита — переменную 6 и т. д. То есть на основном уровне ИОС, получаемых в результате какой-либо операции над двумя ИОС, среди которых хотя бы один ИОС содержит на основном уровне букву Ь, необходимо ставить букву с. Если хотя бы один ИОС из числа тех, над которыми выполняются эти операции, содержит на основном уровне букву с, то результат операции будет содержать на основном уровне букву d, и т. п.

Индексные объекты вида (1) и операции над ними (2) — (3) образуют алгебру, названную нами алгеброй ПИОС, которая основана на теории множеств и позволяет алгебраически описывать ССА (а значит — и весь алгоритм). Для описания ССА необходимо составить для нее последовательность ИОС. После этого составленную ПИОС необходимо упорядочитьсо-гласно возрастанию номеров и согласно условиям выполнения операций композиции, итерации и сложения. При упорядочении двух ИО согласно операции композиции необходимо на первое место ставить тот ИО, у которого немой индекс расположен вверху. Если при этом обнаружатся ЙО, для которых это правило невыполнимо, то такие ИО с «обратным» расположением немых индексов обозначают первый и последний операторы тела цикла.

При выполнении операции композиции в последовательности ИОС не должны нарушаться общие пути в ССА, соответствующей этой последовательности. Это может произойти в том случае, если немой индекс п будет встречаться не только у компонируемых ИОС, но и у других ИОС этой же последовательности.

К операции сложения ИОС (3) это не относится, так как после ее выполнения вершины из ССА не удаляются и пути в ней не нарушаются, т. е. результат операции сложения двух ИОС не зависит от повторяемости индексов складываемых ИОС в других ИОС этой же последовательности.

После всех упорядочений и расстановки знаков операций ПИОС превратится в уравнение, аналитически описывающее ССА. Это уравнение может быть названо индексным уравнением-соответствием (ИУС) и использовано для дальнейших равносильных преобразований.

Индексное уравнение-соответствие для приведенного на рис. 1 примера будет следующим

2 / Зо 4   415.6.

а, "^2 «з + а₂ уа^ а^ . ■■

Представленный в настоящей работе подход к описанию алгоритмов при помощи схем соответствий алгоритмов и индексных уравнений-соответствий позволяет математизировать процесс равносильных преобразований алгоритмов.