Алгоритм анализа числовых последовательностей

При обработке числовых данных часто возникает задача выяснить, подчиняются ли значения элементов имеющейся числовой последовательности какой-нибудь функциональной зависимости. Если удается установить такую функциональную зависимость, то можно сократить объем вычислений при обработке, используя свойства известной функции; найти более простую функцию, значения которой в узлах координатной сетки аппроксимируют имеющуюся последовательность с заданной точностью; экстраполировать числовую последовательность.

В настоящее время существует несколько методов восстановления одномерных зависимостей, которые делятся на интерполяционные и аппроксимационные. Отличием интерполяционных методов является то, что полученная с их помощью функция проходит через заранее заданные точки. Типичным примером глобальной интерполяции (одновременное использование всех изве стных узлов) является использование интерполяционного многочлена. Однако при большом количестве узлов (n > 7) применение такой интерполяции уже не оправдывает себя по ряду причин [1]. Прежде всего, возрастают погрешности из-за того, что интерполяционный многочлен требует гладкости по производным n-го и высших порядков. Поэтому чаще применяют локальную интерполяцию (например, сплайны), которая тоже обладает недостатками. Оба метода (глобальной и локальной интерполяции) требуют большого объема памяти для хранения информации об интерполирующей функции, сравнимого с объемом исходной информации.

Предложенный алгоритм основан на принципах цифровой фильтрации и позволяет выявлять функциональные зависимости в последовательностях чисел. Алгоритм является интерполяционным и представляет решение (найденную функцию) в более простом виде, чем рас- пространенные методы. Процесс цифровой фильтрации описывается выражением вида [2]

NM

У ⁽ n ) = ^ b_kx ⁽ n - k ) - ^ a_ky ⁽ n - k ) ,       (1)

k = 0                    k = 1

необходимо выбрать Ми А, т. е. количество коэффициентов фильтра. Пусть М произвольно и больше единицы, а А=М- 1. Запишем систему уравнений в матричном виде:

РС У,

гдеу(и)- выходная, а x(n) - входная последовательность, а и Ъ - действительные коэффициенты. Выход цифрового фильтра зависит от текущего входа и от некоторого числа предыдущих входов и выходов. Если на вход подать единичный импульс 8(и), равный

где У- исходная последовательность, записанная в виде вектор-столбца, С - вектор неизвестных коэффициентов фильтра:

:

^{8 (} n ) =

1, n = 0,

0, n * 0.

выходом будет являться импульсная характеристика к(н).

Если принять все коэффициенты а_к равными нулю и, таким образом исключить обратную связь, получим циф

ровой фильтр (ЦФ) с конечной импульсной характеристикой (КИХ-фильтр). Импульсная характеристика (ИХ) такого фильтра конечна и ее коэффициенты равны весовым коэффициентам фильтра Ък:

Л( _И )-{Ъ_Й,Ъ„^,Ъ „ }.              (3)

Если есть отличные от нуля коэффициенты а_к, импульсная характеристика становится бесконечной за счет обратной связи, устанавливающей зависимость текущего выходного отсчета отМ предыдущих выходных отсчетов [2]. Системы подобного вида называются фильтрами с бесконечной импульсной характеристикой (БИХ-фильт-ры). В дальнейшем будем рассматривать БИХ-фильтры, потому что они позволяют сопоставить конечное количество коэффициентов и бесконечную последовательность. Импульсная характеристика устойчивого БИХ-фильтра должна со временем затухать, но в нашем случае это не важно, так как работоспособность алгоритма не зависит от того, устойчив фильтр или нет.

Пусть имеется достаточно длинная последовательность чисел У= {у_к} длины L. Сформулируем задачу следующим образом: требуется установить, подчиняются ли значения элементов последовательности (все или только на некоторых участках) какой-то функциональной зависимости.

Предлагаемый алгоритм состоит из двух шагов. На первом для последовательности У необходимо найти БИХ-фильтр, начало импульсной характеристики которого совпадает с У. Найденный фильтр будем называть фильтром, соответствующим последовательности У. Если невозможно найти такой фильтр для всей последовательности, можно разбить ее на части и искать соответствующий фильтр для каждой части. На втором шаге коэффициенты каждого найденного фильтра анализируются, и делается вывод, какой функциональной зависимости подчиняются элементы последовательности, которой он соответствует

Основная задача на первом шаге алгоритма - нахождение коэффициентов а_к и Ъ_к БИХ-фильтра, у которого первые L элементов импульсной характеристики совпадают с исходной последовательностью У. Для нахождения коэффициентов фильтра составим систему L линейных алгебраических уравнений (СЛАУ), воспользовавшись уравнением фильтрации (1). В нашем случае у(н) — У — {у }, а х(п) = 8(и) - единичный импульс. Для построения СЛАУ

а Р - матрица системы, имеющая следующий вид:

P =

N + 1

- У ₀

^- У 1

^- У 0

^^^^^в

L

^^^^^в

- y N

- y N - 1

L

^^^^^в

^^^^^в

^^^^^в

^^^^^в

L

^^^^^в

^^^^^в

^^^^^в

^^^^^в

L

- y L - M

y L - M - 1

1 4 4

4 4 4

4 4

Как видно, матрица системы структурно состоит из

двух частей - правой и левой. Причем левая имеет тепли-

цеву структуру. Размерность матрицы равна Р - L • (М+

+ А+ 1). То есть квадратной она не является, и сразу при

менить какой-нибудь из стандартных методов для реше-

ния системы не представляется возможным, так как они предполагают, что матрица системы квадратная и невырожденная. Подбирать М и А такими, чтобы матрица Р была квадратной, не является приемлемым решением, так как L обычно велико и может достигать сотен тысяч. По

этому предлагается применять следующую методику:

• 1)    сначала рассматриваем только первыеМ+А+1 уравнений системы (4), в этом случае матрица системы уравнений является квадратной, находим ранги матрицыР и расширенной матрицы системы P ;

• 2)    если ранги равны М + А + 1, система имеет единственное решение, и мы можем его найти;

• 3)    когда решение для первых М+А+ 1 уравнений существует и найдено, добавляем к квадратной системе уравнений одно следующее уравнение и находим ранги новых матриц системы - расширенной и обычной;

• 4)    если ранги не изменились, значит добавленное уравнение линейно зависимо от остальных, и оно не делает СЛАУ несовместной и не изменяет решения; поэтому его можно отбросить и добавить в систему следующее уравнение (т. е. фактически заменить i-е уравнение на (i + 1)-е, i >М+А+ 1); затем вернуться к шагу 3;

• 5)    если после добавления i-го уравнения ранги оказались неравны, значит найденное решение справедливо только для (i - 1) уравнений, и только (i - 1) первых элементов У совпадают с началом импульсной характеристики найденного ЦФ. Для выбранных Ми Ане существует другого фильтра, начало ИХ которого совпадает с исходной последовательностью У. В случае если найденное решение неудовлетворительно (например, i значительно меньшеL), есть два возможных пути: либо искать другой ЦФ при больших М и А, либо оставить этот фильтр для первых (i - 1) элементов У, а для оставшейся части У искать другой фильтр.

Замечания к описанной последовательности действий:

- методика оказывается работоспособной, если удачно выполняется шаг 2:

rang(P) = rang( P ) = М+ N + 1. (7)

В остальных случаях справедливо следующее:

• а)    если rang(P) = rang( P ) <  М+ N+ 1, система уравнений недоопределена, поэтому можно отбросить М+N + + 1 - rang(P) линейно-зависимых уравнений, затем дополнить СЛАУ следующими уравнениями из (4) до исходного размера и опять вычислить ранги;

• б)    если rang(P) Ф rang( P ), при данных Ми Nне существует такого цифрового фильтра, у которого начало импульсной характеристики совпадало бы с У;

• -    шаг 4 следует выполнять, пока i <  L;

• -    предполагается, что порядок ЦФ (наибольшее из М и N) значительно меньше длины исследуемой последовательности: max(M, N) <У на части, каждая из которых интерполируется импульсной характеристикой отдельного фильтра (прим. 1).

Пример 1. Дана последовательность У= {0 2 5 9 14 20 27 35 44 54 65 75 84 91 96 99 100 99 96 91 84 75 64 51 36 19 0-18-4-18-4-18-4-18-4-18-4-18-4}. Необходимо найти соответствующий ей фильтр.

ПриМменьшем, чем длина У, не существует фильтра, у которого начало импульсной характеристики совпадает с данной последовательностью. Однако если разбить ее на три части (рисунок), можно для каждой части найти ЦФ с небольшим количеством коэффициентов.

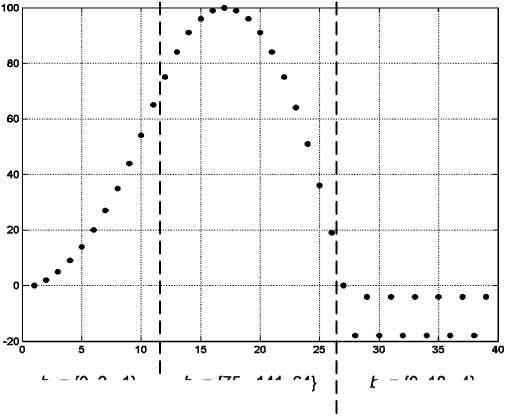
ьк = ^0 18 -4} at={0 -1} bk= -141 64} ak = {-3 3 -1}

Рисунок bk=P 2 -1} ak = {-3 3 -1}

Когда определены Ми N, для которых существует искомый фильтр, решить систему уравнений (4) не составляет труда. Поэтому наиболее важным этапом является выбор MиN. Поскольку целью алгоритма является определение того, подчиняются ли значения элементов последовательности У некоторой функциональной зависимости, можно воспользоваться этим для определения М и N, подходящих для разных функций. Для этого подста вим в исходную СЛАУ вместо yi значения рассматриваемой функции, заданной в общем виде. А затем, меняя М и N, найдем такие, при которых система обязательно будет совместна, т. е. rang(P) = rang( р) (прим. 2).

Пример 2. Найдем Ми N цифрового фильтра, импульсная характеристика которого интерполирует L значений полинома второй степени:y_i = а ■ i² + b ■ i + с, а Ф 0, i = 0,..., L - 1. Для этого подставим выражения^, в Р и р и найдем их ранги. Из вида матрицы Р следует, что каждое из первых (N+ 1) строк линейно независимо от всех остальных, поэтому для краткости при вычислении ранга будем рассматривать только правую нижнюю подматрицу Z матрицы Р размером (L - N - 1) ■ М. Ранг будем искать путем приведения матрицы к простейшему виду при помощи элементарных преобразований. Пусть М = 3, N=2,L = 8.

( -4 a - 2 b - c

- a - b - c

( -4 a - 2 b

-9 a - 3 b - c

-4 a - 2 b - c

- a - b

-8 a - 2 b

Z = -16 a - 4 b - c -9 a - 3 b - c

-4 a - 2 b - c --12 a - 2 b

-25 a - 5 b - c -16 a - 4 b - c

-36 a - 6 b - c -25 a - 5 b - c

-4 a - 2 b - a - b    - c

• - 4 a    -2 a    - a - b

• - 8 a     —4 a   -4 a - 2 b

• - 12 a    -6 a   -9 a - 3 b

• - 16 a    -8 a   -16 a - 4 b

• -    a - b      - c

• - 3 a - b   - a - b - c

• - 5 a - b -4 a - 2 b - c ~

• - 7 a - b -9 a - 3 b - c

• - 9 a - b -16 a - 4 b - c

• - 2 a - a - b-

0    -2 a - a - b

0     0

0     00

0     00

• -9 a - 3 b - c     -16 a - 2 b

• -16 a - 4 b - c l 1-20 a - 2 b

(—2 a — a — b— c

0    -2 a - a - b

~ 0     0     ^- 2 a ~

0     0

0     0

/ X/

Так как а Ф 0, ранг матрицы Z всегда равен 3.

Матрица

( - 4 a - 2 b - c    - a - b - c        - c

- 9 a - 3 b - c   - 4 a - 2 b - c    - a - b - c

Z = - 16 a - 4 b - c - 9 a - 3 b - c

- 4 a - 2 b - c

- 25 a - 5 b - c - 16 a - 4 b - c - 9 a - 3 b - c

- 36 a - 6 b - c - 25 a - 5 b - c - 16 a - 4 b - c

9 a + 3 b + c ^

16 a + 4 b + c

25 a + 5 b + c

36 a + 6 b + c

49 a + 7 b + c

/ аналогичными преобразованиями приводится к виду

2a - a - b - c 0 0 —2 a - a - b 0 0 0 —2 a 0 0 0 0 0 0 0 0 0 т. е. rang( Z ) = rang(Z), при любых значениях а, b и с. При этом rang(Z) максимален, а значит М меньше трех уже брать нельзя. Если взять Мбольше трех, то М- 3 столбцов после элементарных преобразований станут полностью нулевыми и ранги останутся равными трем. Таким образом, М> 3 тоже приемлемо, но чем меньше М, тем лучше (так как меньше решаемая СЛАУ и проще фильтр).

С выбором N аналогичная ситуация: при N меньшем, чем в разобранном примере, ранги получаются неравными, а при большем N- не изменяются.

Таким образом, для интерполяции последовательности значений любого полинома второй степени достаточно цифрового фильтра с шестью коэффициентами, из которых половина - коэффициенты обратной связи.

Аналогичным образом могут быть получены минимальные значения Ми N для различных функциональных зависимостей, которым могут подчиняться члены исследуемой последовательности (табл. 1).

Приведенные в табл. 1 зависимости являются достаточно простыми и скорее всего члены исследуемых последовательностей будут подчиняться им в редких случаях. Гораздо более реальным представляется случай, когда значения ИХ у. подчиняются сумме простейших функций. Назовем функции, для которых существуют конечные Ми Nи они характеризуются функциями, известными алгоритму. Если значения коэффициентов импульсной характеристики ЦФ подчиняются конечной сумме таких функций, то для такого фильтра могут быть найдены М и N и он может быть идентифицирован (аналогично прим. 2). ПримерыМи^Удля фильтров с более сложными импульсными характеристиками приведены в табл. 2.

Чем более сложна функциональная зависимость, тем больше коэффициентов у соответствующего фильтра. Однако рост числа коэффициентов невелик.

Когда выполнен первый шаг алгоритма и последовательность разбита на части, каждой из которых сопоставлен свой цифровой фильтр, можно перейти ко второму шагу. Он заключается в определении вида функциональной зависимости по характерным особенностям коэффициентов ЦФ.

Для некоторых классов функциональных зависимостей сам вид зависимости возможно сразу определить по значениям коэффициентов обратной связи а., а все параметры (константы) функции определяются по коэффициентам Ъ. Назовем такие функции простыми. Для других (назовем их сложными) необходим более сложный анализ, так как в них информация о параметрах функции влияет и на коэффициенты обратной связи (табл. 3).

Коэффициенты обратной связи а . зависят от вида функции, а не от ее параметров. Например, фильтры (рисунок), соответствующие первым двум частям последовательности, имеют одинаковые коэффициенты а . = (-3 3-1). Значит, элементы каждой из этих частей подчиняются квадратичной зависимости, что вполне прослеживается на графике.

Коэффициенты Ъ. для простых функций однозначно определяются параметрами анализируемой последовательности (табл. 4).

Поскольку коэффициенты Ъ . связаны с параметрами искомой зависимости линейным преобразованием, а также минимальное их количество равно количеству параметров, то выразить параметры из коэффициентов фильтра не составляет труда.

Таблица 1

Зависимость		M	N
Линейная	у = kx + b	2	1
Квадратичная	у = ax2 + bx + с	3	2
Кубическая	у = ax ’ + bx2 + ex + d	4	3
Полином 4-й степени	у = ax4 + bx3 + ex2 + dx + e	5	4
Периодическая, с периодом Т	произвольная	Т	Т- 1
Показательная	у = ka + e	2	1
Синусоида	у = a - sin(bx+ e) + d	3	2

Таблица 2

Зависимость		M	N
Сумма линейной и периодической с периодом 2	у = ax + b(-1)x + e	3	2
Сумма квадратичной и периодической с периодом 3		5	4
Сумма двух синусоид	у = k1-sin(f1x + ф 1) + k2-sin(/ 2 x + ф 2) + e	5	4
Сумма показательной, квадратичной и синусоидальной функций	у = k1-abx + kyx2 + k3-x + k4-sin(^ + ф) + e	6	5
Сумма трех синусоид	у = kj-sin(/ j x + ф 1) + kysin^x + ф 2) + + kysin^x + ф 3) + e	7	6

Таблица 3

Зависимость		M	Коэффициенты a ,
Линейная	у = kx + b	2	(-2 1)
Квадратичная	у = ax2 + bx + e	3	(-3 3 -1)
Кубическая	у = ax3 + bx2 + ex + d	4	(-4 6 -4 1)
Полином 4-й степени	у = ax4 + bx3 + ex2 + dx + e	5	(-5 10-10 5-1)
Периодическая, с периодом Т	произвольная	Т	(00...00-1)

Таблица 4

Зависимость		N	Коэффициенты bt
Линейная	у = kx + b	1	(k+b -b)
Квадратичная	у = ax2 + bx + e	2	(a+b+e a-b-2e e)
Кубическая	у = ax3 + bx2 + ex + d	3	(a+b+e+d 4a-2e-3d a-b+e+3d - d )
Полином 4-й степени	у = ax4 + bx3 + ex2 + dx + e	4	(a+b+e+d+e 11a+3b-e-3d-4e 11a-3b-e+3d+6e a-b+e-d-4e 0
Периодическая, с периодом Т	произвольная	Т- 1	(ЖЛ- у т -1 )

Такой же анализ применим к последовательности, значения членов которой подчиняются конечной сумме простых функций. Сумма простых функций является простой функцией. В этом случае так же вся информация о форме зависимости содержится в коэффициентах а, а вся информация о параметрах зависимости - в коэффициентах Ъ соответствующего цифрового фильтра (табл. 5).

Однако встречаются сложные функции, для которых значения коэффициентов а . соответствующего цифрового фильтра не являются постоянными, а зависят кроме вида функции еще и от ее параметров. Тем не менее, хотя в этом случае коэффициенты фильтра связаны с параметрами зависимости нелинейным преобразованием, найти обратное преобразование и выразить параметры через коэффициенты возможно. Рассмотрим выявление сложной функции и нахождение ее параметров (прим. 3).

Пример 3. Коэффициенты ЦФ при минимальных Ми N, соответствующего показательной зависимости у = ка¹ + с равны

Ъ₀ = ка + с, Ъ = - а(к + с), a_t = - а - 1, а₂ = а.

Так, значения членов исходной последовательности являются значениями показательной функции, если для соответствующего фильтра выполняются следующие условия:

М= 2, N= 1, а +а₂ =-1, а₂>0, а₂^ 1.     (8)

Параметры искомой зависимости вычисляются из коэффициентов фильтра следующим образом:

—b — b о a 2 a ₂ (1 — a ₂ )

b + b a = a,, c =------ 2         1 — a 2

.

Сумма двух сложных функций или простой и слож ной является сложной функцией. Это несколько услож няет анализ, так как многие сигналы разлагаются на сумму синусоид, а синусоида является сложной функцией.

Таким образом, для выявления функциональных зависимостей, которым подчиняются члены некоторой последовательности, алгоритм должен обладать некоторой базой знаний коэффициентов а. фильтров, соответствующих простым функциям (табл. 3), а также базой знаний для выявления сложных функций (например, условия (8) для выявления показательной функции). Меняя базу знаний, можно настраивать алгоритм для определенных целей. Например, внеся туда данные только о си нусоиде и суммах синусоид (2.. .А), можно узнать, разлагается ли последовательность на сумму синусоид (аналог Фурье-анализа). Как известно [2], в дискретном Фурье-анализе разложение производится по гармоникам 25k, где к = 0, 1,..., L/2, а L - количество отсчетов L сигнала, которые могут и не совпадать с реальными гармониками исследуемого сигнала. Использование предложенного алгоритма позволяет произвести разложение не по частотам алгоритма дискретного преобразования Фурье (ДПФ), а по оригинальным частотам сигнала, которых, как правило, гораздо меньше, чем L / 2.

Кроме возможности настройки под определенные цели, предложенный алгоритм выгодно отличается от распространенных методов интерполяции тем, что найденная интерполяционная функция имеет меньше коэффициентов. Например, интерполяционный многочлен, соответствующий первой части последовательности У (прим. 1), содержит 11 коэффициентов (столько же, сколько исходных элементов). В то время как соответствующий ЦФ - только 6 коэффициентов. А если из коэффициентов ЦФ восстановить искомую функцию (ах² + Ъх + с), то коэффициентов останется всего три (а, Ъ и с). Это позволяет использовать рассмотренный подход для сжатия данных [3].

Таким образом, в статье предложен двухшаговый алгоритм поиска функциональных зависимостей в числовых последовательностях. Описана методика идентификации БИХ-фильтра по L первым элементам импульсной характеристики, используемая на первом шаге. Установлена взаимосвязь между видом зависимости и коэффициентами соответствующего цифрового фильтра.