Алгоритм численного решения симметрических T-гиперболических систем с постоянными коэффициентами на односвязной двухмерной области
Автор: Давлатов Ш.О.
Журнал: Мировая наука @science-j
Рубрика: Основной раздел
Статья в выпуске: 6 (87), 2024 года.
Бесплатный доступ
В этой статье исследована смешанная задача для симметрических t-гиперболических систем с постоянными коэффициентами. В ней обоснована схема конечных элементов в случае равномерной сетки. Разработана программа расчета численного решения.
Метод конечных элементов, алгоритм, смешанная задача, гиперболическая система, базисные функции, неявно-разностная схема
Короткий адрес: https://sciup.org/140306436
IDR: 140306436
Текст научной статьи Алгоритм численного решения симметрических T-гиперболических систем с постоянными коэффициентами на односвязной двухмерной области
Постановка смешанной задачи для двумерных симметрических t-гиперболичес ких си стем с постоянными коэффициентами.
Пусть Q c R . В области G= [(t,x,у)A e (О,T), (x,у) g Qj найти вектор- функцию и , удовлетворяющую системе
Ади(х,у^ +Bdu(x,y,t) + Coll<x^O + £^ (1)
C t (. А С V с граничными
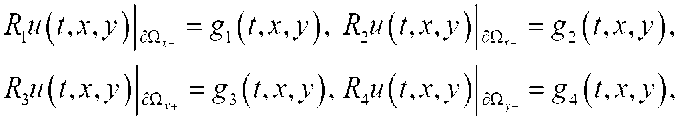
и начальным
u(o,x,y) = uo(x,y) , (х;у)еО. ; (3)
условиями. Здесь A,B,C~ действительные постоянные симметричные матрицы размерности NxN, причем A - положительно определенная; D- произвольная действительная постоянная матрица размера NxN; R{,R2^R^R4~ постоянные матрицы, количество столбцов которых равно N , а количества строк матриц rvr2
равны количеству положительных и отрицателных собственных значений матрицы A-'B соответственно, а количества строк матриц r„r4 равны количеству положительных и отрицателных собственных значений матрицы A 'C соответственно; Sv Si? Si’ g^ заданные вектор-функции, согласованные с размерностью матриц ^,в2,в3,в4 соответственно; aQT+,5Qv - части границы an , где ставятся условия, соответствующие положительным и отрицательным собственным значениям матрицы A-]B соответственно, а ao^ao^.- части границы an , где ставятся условия, соответствующие положительным и отрицательным собственным значениям матрицы A ^C соответственно; 1ф,У)~ заданная вектор-функция; u(t,x,y) = (ul,u2,...,uM)T - неизвестная, а Рф,У) = (/ф2,---,/м)' ~ заданная вектор-функция.
Q - Аппроксимация области.
Двумерная ограниченная область аппроксимирована следующим образом. При описании границы области в качестве составляющих ее частей могут использоваться отрезки прямых и дуги окружностей.Началом некоторой части границы S считается та ее концевая точка, при движении из которой по S область остается слева. Отрезки прямых определяются двумя точками – концами, а для дуг окружностей дополнительно задается точка центра окружности.
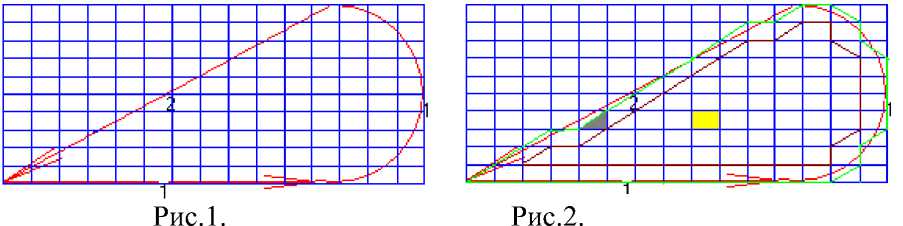
Область Q заключим в наименьший прямоугольник со сторонами, паралельными осям Ox и Oy : . Проведем прямые x = xi = a + hyi (i = O,...,NJy=^) , y = y/=c + hvj (j = Q,...,Ny,hy=^-^-) пересекающие отрезки, соответсвенно, [a;b] , [c; ^ ] . В результате область Q покроется равномерной сеткой (рис.1).
У = У,- =c + hvj , называемую
Точку пересечения прямых x = Xj =a + hy и узлом сетки, обозначим через .
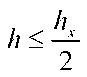
или
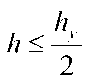
1-определение. Узел, находящийся на расстояние от 6Q , или лежающий на dQ называется граничным узлом.
На рисунке 2 граничные узлы соединены линией зеленого цвета.
2-определение. Узел, лежащий внутри области Q и являющийся соседным узлом граничного узла, называется околограничным узлом.
На рисунке 2 околограничные узлы соединены линией коричневого цвета.
3-определение. Узел, лежащий внутри области Q и не являющийся соседным узлом граничного узла, называется внутренным узлом.
4-определение. Узел, не лежащий внутри области Q и не являющийся граничным узлом, называется внешным узлом.
Сетка разбивает область ^^h на части (элементы). Каждый элемент является прямоугольником (на рис.2. желтого цвета) или треугольником (на рис.2. серого цвета) . Э лемент обозначим через К . Элементы, одной из вершин которых является узел My , называются элементами этого узла. Объединение этих узлов обозначим через . Тогда справедливо равенство .
Построение неявной разностной схемы для задачи (1)-(3)
Построим неявную разностную схему для системы (1).
Отрезок [OX] разобъем на X частей:
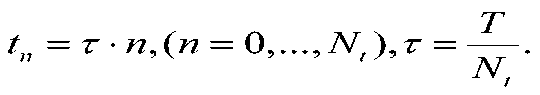
Будем искать приближенное решение смешанный задачи (1)-(3) на каждом слое tn по времени в виде < = 11!, V,^y)= X "№j (X’ У^. Здесь Q.^y) базисные функции, в узле Щу,у^ значение Q^y) равно i , а в остальных узлах - 0,
^ = и(у,угО = ^^^ = (11"^,...^ .
Аппроксимируем систему (19) в узле Mg т.е. в системе (1)
du u(t + T,x,v}-u(t,x,y)
производную по времени аппроксимируем отношением ot т вместо u(t,x,y) подставим ^Р^п^’У) , каждое уравнение полученной системы умножим на QiS^y} и проинтегрируем по ^u .Здесь ^'7 - объединение всех элементов узла My . В итоге получим неявную разностную схему:
(a„(A + rD) + pIJrB + /„rC)y +
У„(а +гл)+ рМ1тв+r.^cy^ +
Уч»(А + ^) + РммтВ + Г^гСУ'У + yaA + rDi + ^rB + ^TC)^
(су^Л + rD) + P^B + Y^j^)11г-U+l +
(a^A + rD)^^^
(a^A + tD^^tB + Y^Cy^ + (4)
[a^A+rD^p^B + r^TCy^
Y^,-SA + ^) + PMJ_yB + 7м,^С}и'ш,л =
|
r^Fr |
+ тА(а^ + cc__ 7C . + «HJy+Iw;i>+J + |
|
aij+iuy+i |
+ °A-l j+[Ut-[ J+l + at-[ JUi-l J + ^i-l j-lUi-l j-l + |
|
^ aMj-YlMj-\^ (^p^jJ^^ ■ |
Здесь
^j^ \ Qy(x,y)dxdy, Д = | у у с дО (х, у)
А = f ^——Qyx^dxdy, А дУ
дО.(х, у) ^-—Q^y)dxdy,
Qy = J Q^xyydxdy.
Граничных и начальных условий аппроксимируем следующим образом
„+!’
11+1’ и+Р
|
■wj |
8у,х+ — ^1 (С?+1 Ар. |
|
Х^У]} |
— ^2(^+1 АА |
|
x^j) |
dQhr+ — ^з(А+1АА |
|
^yj) |
3Q- — ^4 (А+1 АА |
У^М^у^еХ!^-, 'У^М^у^ед^у у’Ум^у^Ед^.у ^^М^у^Ед^у
при / = 0:
Uyv^X-^yj ) у \, у j , м^УУ^ь.
В качестве базисной функции возьмем функции Q^y^P,^^ где
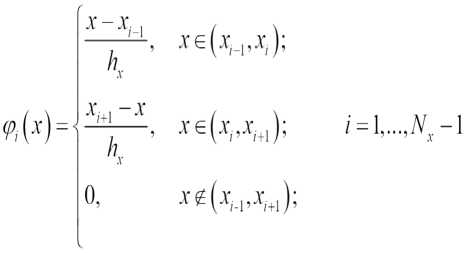
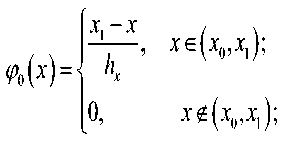
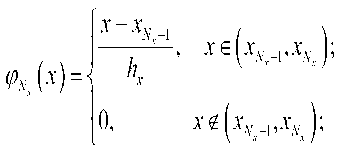
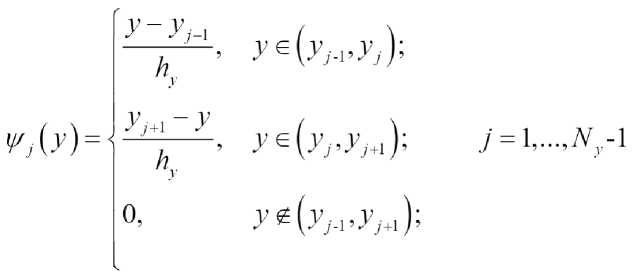
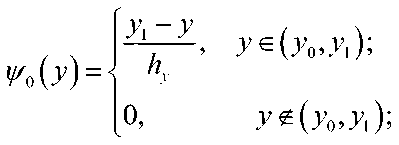
|
' у-Уу-1 |
|
|
^Ы=< |
0, |
Считая, что найдено приближенное решение смешанный задачи до tn (w = 0,1,2,...) слоя включит ел ьно, для нахождения приближенного решения смешанной задачи на слое ^1+1 объединим систему разностных уравнений (4) каждого узла My^M^y^Ed^ и граничные условия (5) каждого граничного узла M^y^ E д£\ . В итоге получим систему линейных уравнений относительно компонентов векторов 111/ . Для того чтобы эта система линейных уравнений была замкнута, на граничнах узлах MyMfxyyJed^ , для компонентов решения n(x.yj) , для которых не поставлены граничные условия, возмем соответсвующие разностные уравнения из системы (4). В итоге получим замкнутую систему линейных уравнений. Решив эту систему методом главных элементов, получим численное решение задачи (1)-(3).
Следующая теорема, показывающая условную устойчивость разностной схемы, полученной методом конечных элементов для смешанной задачи (1)-(3).
Теорема. При выполнении условий разностная задача (4)-(6) имеет единственное решение ^h , причём при любых
^’^У и при всех 11 < выполняется неравенство
Здесь ll"Lm=./К“И’ , F = maxIlF" , ^ ^X^ + ЛуС , n = (nx,ny)- внешняя нормаль к .
На основе этих схем создана программа, решающая численно задачу (1)-(3) и рисующая график решения. При этом в случае не выполнения условий устойчивости (9) программа информирует об этом. Созданная программа проверена на основе вычислительных экспериментов в модельных задачах.
Пример:
Дано система
Q = {(x, y): 0 < x < 2,0 < у < 2} да
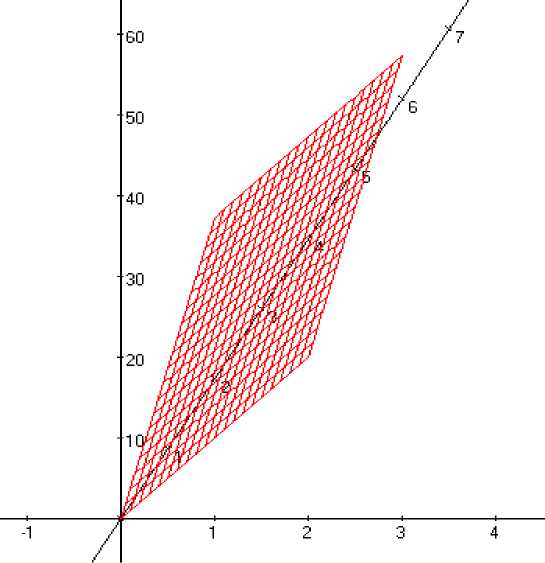
= О- -I- >o x-2 да z/, = -yu2 + (y2 + 4y)/ ; у = 0 да IIt = It2 ~Xt; У = 2 да u2 = -2xii} + (4x2 + x + 2)1; и начальными данными r = 0 Найти численное решение системе удовлетворяющей граничных и начальных условий методом конечных элементов. Точные решения системе следующие щ = xyt II-, = (.V + y)t Если количество разбиений по времени nt = 5 , количества разбиений по х и у соответственно равны wr = 20, /7 v = 20 ,то тогда разность между точным и приближенным решением во время Z = 10 равно ||г/ - v|| = 0,0823485 .Где Лг/] Л f ri Л ^ ' V J точное решение, приближенное решение. Рис. 3. Графиг . Рис. 4. Графиг Ъ Литературы: 1.Годунов С.К. Уравнения математической физики. М.:Наука,1979,372с. 2 .С.К.Годунов, А.В.Забродин и др.Численное решение многомерных задач газовой динамики. М.:Наука,1976. 75с. 3 .Марчук Р.И., Агошков В.И. Введение в проекционно-сеточные методы.-М.:Наука,1981.416 с. 4 . Applied Finite Element Analysis. Larry J. Segerlind. John Wiley & Sons, Inc. 1976. 289-308 с. "Мировая наука" №6 (87) 2024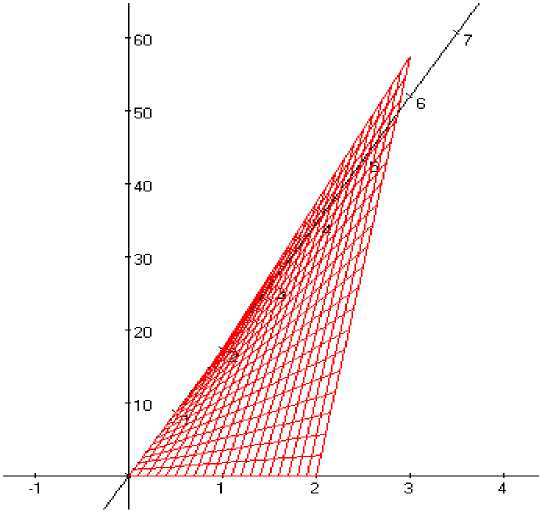
Список литературы Алгоритм численного решения симметрических T-гиперболических систем с постоянными коэффициентами на односвязной двухмерной области
- Годунов С.К. Уравнения математической физики. М.: Наука,1979,372с.
- С.К.Годунов, А.В.Забродин и др.Численное решение многомерных задач газовой динамики. М.: Наука,1976. 75с. EDN: UESERL
- Марчук Р.И., Агошков В.И. Введение в проекционно-сеточные методы. -М.: Наука,1981.416 с.
- Applied Finite Element Analysis. Larry J. Segerlind. John Wiley & Sons, Inc. 1976. 289-308 с.


