Алгоритм численного решения задачи Шоуолтера-Сидорова для систем леонтьевского типа

В [1, 2] предложен численный алгоритм решения задачи Коши

и(О) = ио (1) для линейной системы обыкновенных дифференциальных уравнений й = Su + g, (2) основанный на идеях теории полугрупп операторов. Здесь S - квадратная матрица порядка и. В [3, 4] этот подход был распространен на задачу (1) для вырожденной системы уравнений

Lit = Ми + / (3) с использованием идей теории вырожденных полугрупп операторов [5] (здесь L и М - квадратные матрицы, порядка и, причем det L = 0). Одним из важных случаев системы (3) является хорошо известная система В .В. Леонтьева «за-траты-выпуск» с учетом запасов (см. в [6]), поэтому в [3] было предложено такие системы уравнений называть «системами леонтьевского типа».

Простота предложенного в [3, 4] алгоритма обеспечивает высокое качество получаемого программного продукта, что выгодно отличает данный алгоритм от использовавшихся ранее методов Эйлера, Рунге-Кутта, итерационных и других методов [7-9]). Основным недостатком этого алгоритма (как впрочем, и всех остальных)

является принципиальная неразрешимость задачи (1) для системы (3) при произвольных начальных векторах ы₀ e SR”. Эта трудность преодолевается, например в [3], где вектор-функция / :[0,Т]->91" постоянная, введением множества допустимых начальных значений, понимаемых как фазовое пространство системы (3). В [4] при снятии условия постоянства вектор-функции / налагаются условия согласования / с начальным значением и₀ . Заметим, что условия согласования в том или ином виде имеют место и во всех других алгоритмах.

Для условий согласования (как и для построения фазового пространства) необходимы проекторы, которые либо выражаются через контурные интегралы от матриц-функций, либо являются пределами матричных последовательностей. Ввиду неустойчивости любого проектора относительно малых возмущений такое вычисление матрицы проектора очень затруднительно. Поэтому, например в [10], при построении системы (3), моделирующей экономику коммунального хозяйства, пришлось ограничиться малыми городами, т.е. такими, где матрицы L и М имеют порядок не больше 10. Именно малость порядка матриц L и М сделало возможным вычисление проекторов «вручную».

Между тем в современной математической литературе существуют попытки теоретического осмысления так называемых «неклассических» задач для системы (3) [11, 12], основным достоинством некоторых является однозначная разрешимость при любых начальных данных w0 е 91”. Разработка численных алгоритмов решения таких задач позволит избавиться как от трудоемкого построения фазового пространства (и не менее трудоемкой редукции системы (3) к системе (2), заданной на нем), так и от трудоемкой проверки условий согласования. Основная цель данной статьи - построение алгоритма численного решения задачи Шоуолтера-Сидорова aL-M^ 'zj (и(О)-ио) = О для системы (3) (числа аир вычисляются на первом шаге алгоритма). Статья кроме введения и списка литературы содержит две части. В первой дается теоретическое обоснование алгоритма, а во второй приведены основные этапы вычислений.

Пусть L и М - квадратные матрицы порядка и, причем, следуя [13], гл. XII, п. 2, пучок матриц pL-M назовем регулярным, если существует число 2 6 С такое, что det(2Z -Л/) * 0 . Заметим, что условие регулярности пучка матриц эквивалентно условию L -регулярности матрицы М [3, 4]. Поэтому, как показано в [5], гл. 4, при условии регулярности пучка существуют единственным образом определяемые матрицы Н, S, М_о, Ц, Q порядка п, такие, что L-резольвента (pL-M)”^x матрицы М разлагается в ряд Лорана

(PL-М)"1 =t,^HlMQ(l-Q) + 1=0

V^p-'S^Q                 (4)

/=1 в окрестности бесконечно удаленной точки, причем Н - нильпотентная матрица со степенью нильпотентности р, Q - идемпотентная матрица, ММй, MQM, ЦЬ и ЬЦ - диагональные матрицы с нулями и единицами на главной диагонали. Поскольку det(2Z-Af)^O, то многочлен det(2Z-A/) = O имеет не более п различных нулей, которые расположены в круге радиуса а, а значит, при |ц| > а разложение (4) имеет место. Точка оо называется устранимой особой точкой L -резольвенты матрицы М, если р = О в (4); и полюсом порядка р е N в противном случае. В дальнейшем, немного отходя от клас сического стандарта, будем называть устранимую особую точку полюсом порядка нуль. Итак, пусть пучок pL-M регулярен, и оо - полюс порядка р е {0} uN; тогда можно выбрать число а и рассмотреть задачу Шоуолтера-Сидорова

^Wy (w(O)-wo) = O,           (5)

для системы уравнений леонтьевского типа

Ьй = Ми + f,                        (6)

где R^M^^aL-М^ ¹L -правая L-резольвента матрицы М , в отличие от ее левой L -резольвенты Ь^М^ЦаЬ-Му¹, а /:[0,Т]^91" -некоторая вектор-функция.

Решением системы (3) называется вектор-функция u_Q еС¹((0;Т);91")пс([0;Т];91”), удовлетворяющая уравнениям системы. Решение системы (6) называется решением задачи (5), (6), если оно вдобавок удовлетворяет уравнениям (5). Имеет место [5, гл. 4]

ТЕОРЕМА 1.1. Пусть пучок pL-M регулярен, pe{0}uN - порядок полюса L-резольвенты матрицы М, вектор-функция /: [0,Т] -» 91” такая, что ^Ь„(М)У f е С^[0; Т]; 91”), а I - ^L^ (М)У f е С^¹ ((0; Т); 91") п С^р ([0; Т]; 91" ). Тогда при любом и₀ е 91” существует единственное решение задачи (5), (6), которое к тому же имеет вид

«(О=-£ ™о¹ (I - qV⁹4o+u*u₀ + q=0

+jR‘-^sQf(s)ds. о

Здесь

y

R* =Уя1\И-мУхец,ар, Y

Y контур у = ^p e С: |ц| = r > aj. Контурные интегралы не очень удобны в численных расчетах, поэтому в [3, 4] предложен другой подход, основанный на аппроксимациях типа Уиддера-Поста [5, гл. 2]. Именно справедлива

ТЕОРЕМА 1.2. Пусть пучок pL-M регулярен, pe^OjuN - порядок полюса L-резольвенты матрицы М. Тогда lim к->«:

Г ,      *|(р+1)

lim AZf(AZ)

£->00 L         J

= Q,

k(p+i)-i

lim к-»<»

L------

. ^O + D

М L

xZ----- = R*.

I   *(/? + !) )

Теперь пусть пучок pL-M регулярен, pejO^uN - порядок полюса Z-резольвенты

матрицы М в

точке оо. Фиксируем Т е 91.

/g(O,T), ZgN и положим г,                 ч _1 i^Cp+I)

и*к =

L-

-------L

Построение алгоритма начнем с допущения, что det М *0. Это допущение не ограничивает общности предыдущих рассуждений. Действительно, при условии регулярности пучка pL-M , можно сделать замену и = e^v в уравнении (3) и перейти к уравнению

Lv^M-XEy+e^f ^ того же вида, что и (3), но det(AZ - AZ) ^ 0. Обратный переход от решений системы (7) к решениям системы (3) очевиден.

На первом шаге алгоритма нужно найти числа а е 91 и р g {0} и N. Можно разумеется, разложить Z -резольвенту матрицы М в ряд (4) и тем самым сразу же найти эти числа. Однако, существует другой менее трудоемкий путь. Рассмотрим многочлен det(//Z - М) = апрп + ап_хрп-х + . + ахр + а0 . Поскольку ап = detZ, то а„ = 0. Далее, коэффи

\

циент а, есть сумма слагаемых, каждое из кото

Rk =

L---—

. ^ + 1)

V¹ М\ L

-|*(r+i)-i

рых есть произведение одного из миноров порядка I матрицы L на число, 7 = 1,..., и-1,

х L-----М

I ^ + 1) .

а0 = det(-AZ). Поэтому степень многочлена det(//Z-AZ) не выше rankZ, т.е. ранга матрицы Z. Итак, det(//Z-AZ) = aqpq + aq_xp4-x + ... + ахр + а0,

Выберем вектор ы0 с 91”, вектор-функцию / G С^1 [(0; Т); 91" ) n С* ([0; Т]; 91" ) и построим вектор-функцию ик (О = -f Я’М0-1 (I-Q^^w + u«kUo + q=0

+ р?ГаЖ)Д. О

ТЕОРЕМА 1.3. Пусть пучок pL-M регулярен, pG^OjuN - порядок полюса L-резольвенты матрицы М в точке оо. Тогда существует константа С = C(L, М, Т) g 91+ такая, что

||и(0-м4(0|

с

< — при всех

7g[0;T],

и₀ G 91^й, и f g С⁷’*¹ ((0; Т); 91^й ) п С^р ([0; Т]; 91" ).

Доказательство теоремы основывается на оценках г . пО+i) II Й                       II Т II

[КИ -ф£—_^|«i(„)|

^рь-м^1 м^

взятых из [5, гл. 2], где Д g 91+ где q = deg det(/zZ - M) < rank L, поэтому если

взять число a g 91 таким, что

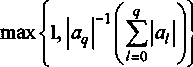
то det(aZ - AZ) ^ 0, и значит, существует матрица (aL -Мух. Далее, считая, что матрица М обратима, представим det(//Z - AZ) = det AZ det(//AZ-1Z -1).

Зная, что порядок полюса в точке оо резольвенты ^pl-M^-XL^ равен нулю, легко найти, что порядок полюса Z -резольвенты матрицы М в точке оо равен n-q. Итак, числа а и p = n-q найдены.

Тогда находя значение к, с которого можно начинать считать приближенные проекторы, получим, что при

1    ”

к>т— _г У Ы+1

мы не сможем оказаться даже вблизи точки Z -спектра оператора М.

Рассмотрим многочлен det(p(/> + 1)Z - /AZ) = aqt4цч (p +1)9 +

-vaq_xtq+xp^Vp-vVy^ + ...+ axt”"1 p + t"a0, где aq Ф 0, q < rank/,. Тогда, учитывая p = n-q при

И

(n-₉) I I I'- ¹      I=q+1

если |/| < 1

/п-9) /77

мы не сможем оказаться даже вблизи точки L - спектра оператора М.

Теоретическая оценка сходимости не позволяет сделать вывод о точности предлагаемого алгоритма. Тем не менее, практические результаты показывают, что уже при числе итераций более ста, результаты вычислений дают не менее точные результаты, чем неявная схема Эйлера или метод Рунге-Кутта. Последний факт позволяет надеяться на развитие предлагаемого подхода как в теоретическом, так и практическом аспектах.

Операторы L и М зададим матрицами

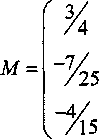
-х

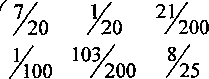
О

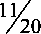
-70836357

Если переобозначить L = B,M = У-А, то матрицы В и А почти совпадут с матрицами из классического примера [6]. «Почти» означает, что элементы тгг и /и23 подобраны специально с целью упростить вычисления и отличаются от приведенных в примере чисел 22/25 и -3/5 на величины

22 -252291

22 25 11996000

-3   1139643

=---.                       (о)

23   5 119960000

В.В. Леонтьев рассматривал взаимосвязи между тремя отраслями экономики: сельским хозяйством, промышленностью и домашними хозяйствами. Элемент ау матрицы А означает количество продукции i -й отрасли, необходимой для производства единицы продукции j -й отрасли. Элемент Ьу матрицы В представляет определенный технологический запас особого типа благ - машин, механических инструментов, промышленных зданий и сооружений, рабочих запасов первичных и промежуточных материалов, производимых отраслью, который используется в отрасли j для производства единицы ее продукции. Другими словами, каждый столбец матрицы В описывает потребность некоторой отрасли в физическом капитале (в расчете на единицу ее валового выпуска) таким же образом, как соответствующий столбец матрицы А описывает ее затраты. Именно поэтому последняя строка матрицы В содержит только нулевые элементы, так как труд невозможно запасти.

Перейдя к расчету системы (3), найдем L - спектр оператора М a^L{M) = {0,2; 2,7}. Именно для того, чтобы точки L -спектра оператора М были рациональными, сделаны поправки (8). Точки L -спектр оператора М в исходном примере иррациональны и отличаются от найденных не большее, чем на одну сотую.

Далее по формулам, приведенным в первой части статьи, построим точное и приближенное решение. Приведем точное решение и результаты счета по алгоритму без комментариев, взяв при этом в качестве / = (2/, It, 2?) (табл. 1,2).

Таким образом, рассмотренный в данной работе алгоритм позволяет численно решать задачу Шоуолтера-Сидорова с достаточной степенью точности: расхождения в точном и приближенном решении начинаются с тысячных долей.