Алгоритм цифровой поддержки работоспособности малогабаритных аэродинамических экспериментальных установок

Введение. Эксперимент представляет собой один из ключевых методов научных исследований, однако при этом возникает проблема невозможности учета всех погрешностей и неточностей, особенно если речь идет о модельных экспериментах. Для уменьшения влияния вышеописанных факторов видится необходимой разработка алгоритмов и методов цифровой поддержки жизненного цикла экспериментальных установок, для чего над их точными компьютерными копиями должны проводиться вычислительные эксперименты, результаты которых могут быть учтены в комплексной методике расчета, нивелирующей погрешности физического испытания.

При проектировании зданий и сооружений сложной геометрической формы актуальным является вопрос корректной оценки аэродинамической нагрузки при взаимодействии с атмосферой [1–6]. Нормативные методики [7, 8] не всегда позволяют корректно провести полноценный учет ветровых воздействий [9], что приводит к необходимости проведения физических и компьютерных экспериментов, и, следовательно, к созданию точных масштабных копий проектируемых зданий [10–13].

Формообразование объектов сложной геометрической формы является первостепенным пунктом при изучении аэродинамических взаимодействий, анализе ветровых нагрузок и прочих задачах архитектурно-строительной аэродинамики. В классической аэродинамике геометрическое подобие не является подобием аэродинамическим ввиду необходимости соблюдения подобия чисел Рейнольдса модели и проектируемого здания. При этом в строительной аэродинамике исследование проводится при малых скоростях ветрового потока, в результате чего отношение чисел Рейнольдса пропорционально линейному масштабу моделирования, т. е. геометрическое подобие практически гарантирует аэродинамическое.

Физический эксперимент на ветровые нагрузки проводится над точными геометрическими копиями проектируемых объектов в аэродинамических трубах. Использование крупногабаритных аэродинамических труб обеспечивает высокую достоверность результатов эксперимента [14]. При этом такие установки являются сложными инженерными объектами, занимающими большие площади и требующими крупных материальных затрат. Аналогом крупногабаритных труб являются трубы малого диаметра, но вследствие их размера такие трубы ограничены в мощности [15]. Ветровой поток в них менее равномерный, в результате чего появляются неточности в результатах эксперимента, из-за которых труба считается неприменимой. Целью исследования является создание цифрового двойника, который позволит не только констатировать несовершенства работы, но и визуализировать их, а также качественно и количественно оценить возникающие в трубах малых габаритов недостатки. Цифровым двойником будет являться виртуальный прототип реальной установки, который полностью имитирует её характеристики и внутренние процессы. При этом в данном случае точная цифровая копия создается для аэродинамической трубы и происходящих в ней аэродинамических процессов во время проведения физических экспериментов, а не для полномасштабных зданий и сооружений, как в большинстве задач компьютерного моделирования.

Таким образом, для обеспечения жизненного цикла таких труб возникает необходимость оценки искажений результатов и их учета в дальнейшем расчете с помощью поправочных коэффициентов. Компьютерное моделирование дает возможность проведения цифровой поддержки и обеспечения эксплуатации изучаемой экспериментальной установки.

Материалы и методы. В настоящей статье исследуется установка для проведения аэродинамических испытаний: аэродинамическая труба лаборатории кафедры «Отопление и вентиляция» ННГАСУ (рис. 1), которая относится к вертикальным малогабаритным дозвуковым аэродинамическим трубам с открытой рабочей областью.

Диаметр основного канала составляет 1000 мм; диаметр выходного сечения – 400 мм; длина рабочей области – около 1200 мм (рис. 2). Общие габариты установки: высота – 3100 мм, ширина – 4400 мм. Скорость ветрового потока, создаваемого осевым вентилятором трубы, – до 12 м/с.

Рис. 1. Аэродинамическая труба малого диаметра: 1 – выходное сечение; 2 – входное сечение; 3 – подмакетник

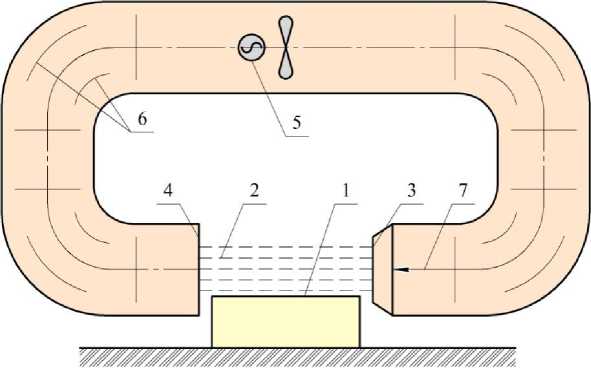
Рис. 2. Схема экспериментальной установки: 1 – подмакетник; 2 – рабочая область; 3 – выходное сечение; 4 – входное сечение; 5 – аэродинамическая труба с осевым вентилятором; 6 – направляющие ребра; 7 – направление ветрового потока

Экспериментальное исследование аэродинамической трубы проводилось без установленных макетов зданий и сооружений в рабочую область с целью изучения распределения выдуваемых ветровых потоков и оценки их потерь, так как трубы с открытой рабочей зоной характеризуются появлением нежелательной циркуляции воздуха и высокой степенью турбулентности.

Измерения производились в плоскости выходного и входного сечения аэродинамической трубы, а также в различных точках рабочей области электронным термоанемометром Testo 405v1.

Следующим этапом исследования аэродинамической трубы является создание цифрового двойника (рис. 3) на основании натурных измерений её рабочих показателей, с точным геометриче- ским соблюдением выходного и входного отверстия трубы и конструкции подмакетника так, чтобы двойник полностью имитировал характеристики установки и её процессы.

Для получения наиболее достоверных результатов при создании точной копии аэродинамической трубы также учитывались основные геометрические особенности и несовершенства установки, например, небольшое отклонение в параллельности плоскостей входного и выходного отверстий (рис. 3, а).

Создание максимально приближенной копии трубы и последующая дискретизация окружающего пространства позволяют считать полученную модель цифровым двойником, моделирование процессов над которым позволяет выполнять ва-

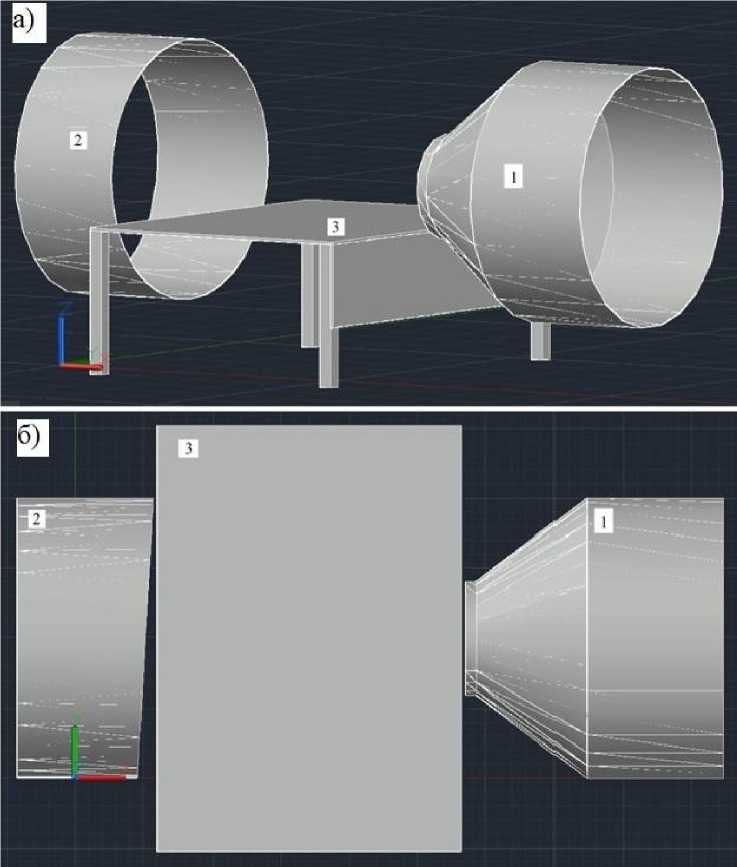
Рис. 3. Геометрическая модель для создания цифрового двойника аэродинамической трубы: а – общий вид, б –вид сверху: 1 – выходное сечение; 2 – входное сечение; 3 – подмакетник

лидацию и обеспечивает цифровую поддержку изучаемой аэродинамической установки.

Компьютерное моделирование аэродинамического эксперимента проводилось в программном комплексе ANSYS с использованием модуля вычислительной гидрогазодинамики ANSYS CFX [16–18], препроцессора ANSYS Meshing и рабочей среды программного обеспечения ANSYS Workbench. Для выполнения моделирования задавались граничные условия:

– размер моделируемой области: по высоте ограничивается полом и нижней поверхностью верхней части трубы; по ширине – к размеру рабочей области добавлены стомиллиметровые выпуски трубы; по длине – с двух сторон от подмакет-ника добавлено по 500 мм;

– все твердые изучаемые поверхности имеют условие «непротекания», при котором обеспечивается свободное проскальзывание воздушных потоков вдоль этих поверхностей;

– вход воздушных потоков в моделируемую область осуществляется через сечение выходной части аэродинамической трубы и имеют начальную скорость 10 м/с (модуль скорости принят по результатам экспериментальных замеров);

– выход воздушных потоков осуществляется через поперечное сечение во входной части трубы и по всей поверхности вокруг неё, где назначается граничное условие отсутствия избыточного давления;

– на остальных поверхностях задаются условия, не влияющие на распределение ветровых потоков;

– расчетная сетка формируется со сгущением к поверхностям выпусков трубы и подмакет-ника.

Результаты исследования. По результатам натурных замеров были построены изополя распределения потоков в двух взаимно перпендикулярных плоскостях (рис. 4, 5).

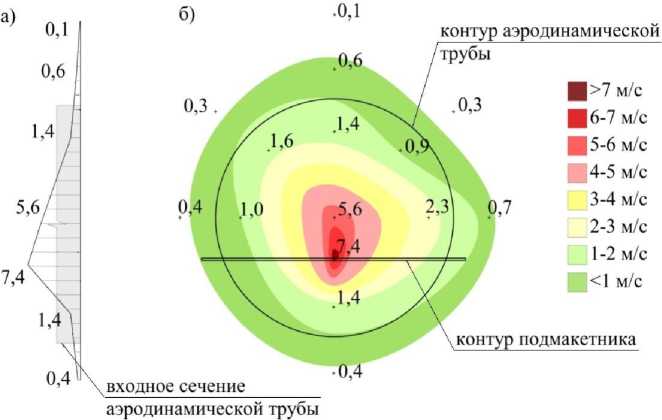
Рис. 4. Профиль (а) и изополя (б) распределения ветровых потоков во входном сечении аэродинамической трубы

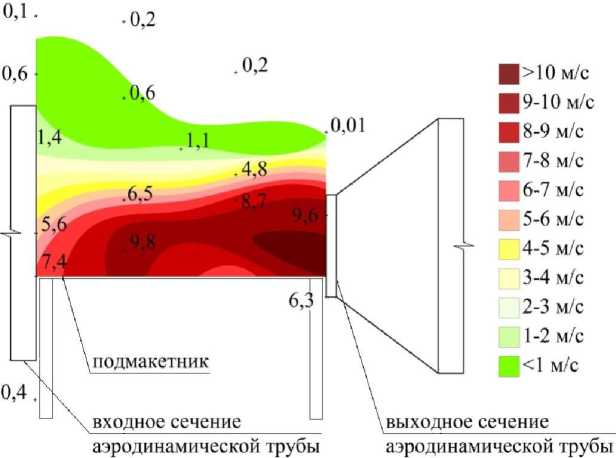
Рис. 5. Распределение ветровых потоков по центральной вертикальной плоскости рабочей области аэродинамической трубы

Распределение основной части ветровых потоков происходит вблизи поверхности подмакет-ника. Полученные результаты объясняют высокую сходимость результатов физического и компьютерного экспериментов большепролетных зданий [19–21], а также подтверждают неточности при сопоставлении данных для высотных зданий [22], так как компьютерное моделирование здания воссоздает воздействия на него в условиях «натурного» эксперимента, в то время как масштабные геометрические копии выходят за пределы однородного распределения ветрового потока в рабочей области аэродинамической установки.

Проведенное компьютерное моделирование распределения ветровых потоков в цифровом двойнике аэродинамической трубы показало достаточно близкие результаты с проведенным физическим экспериментом (рис. 6, 7).

По распределению векторов скоростей в центральной вертикальной плоскости определяется снижение их модулей по высоте и при приближении к входному отверстию трубы (см. рис. 6). При столкновении со стенкой подма-кетника часть потоков устремляется вниз, что также подтверждается измеренной анемометром скоростью (см. рис. 5).

Оценивая распределение векторов скорости в параллельных плоскостях на поверхности стола – подмакетника (рис. 7, а) и выше (рис. 7, б), результаты компьютерного исследования оказываются

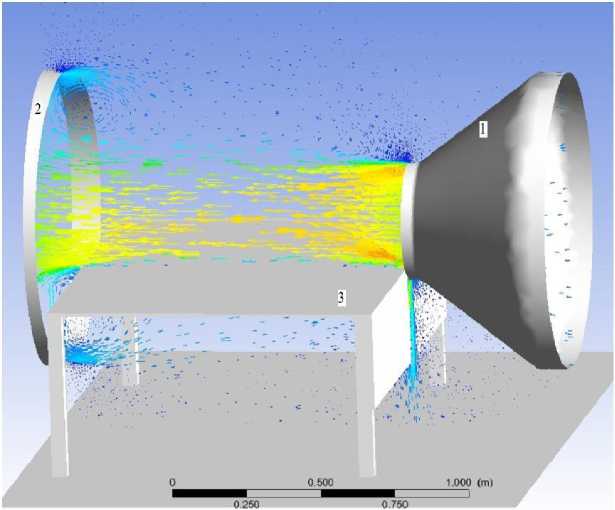
Рис. 6. Распределение ветровых потоков по центральной вертикальной плоскости в рабочей области аэродинамической трубы: 1 – выходное сечение; 2 – входное сечение; 3 – подмакетник

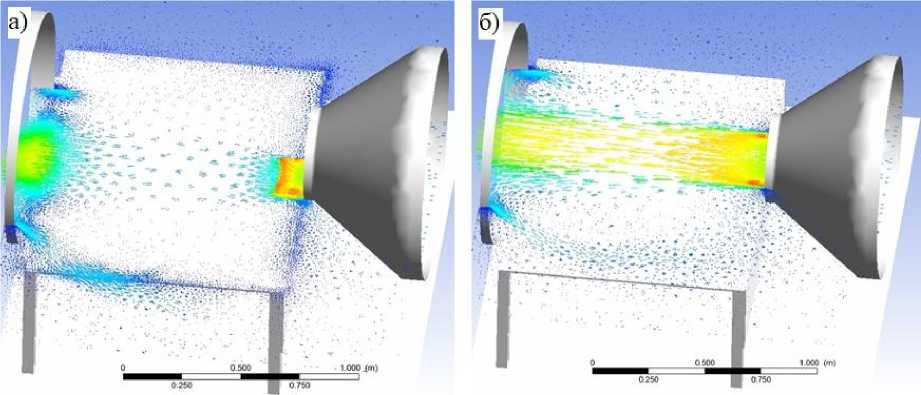
Рис. 7. Распределение ветровых потоков на поверхности подмакетника (а), в горизонтальной плоскости выше (б)

сопоставимы с ранее полученными экспериментальными данными. Наибольшая скорость потока наблюдается при столкновении с поверхностью подмакетника, далее участок небольшого затухания скорости и снова её увеличения. Повторяется волновое движение потока, полученное экспериментально.

Полученные результаты дают возможность всесторонне проанализировать распределение ветровых потоков в аэродинамической трубе, что позволит в дальнейшем провести верификацию данных модельных экспериментов в ней для оценки и создания методики учета погрешностей по разработанному алгоритму (рис. 8).

Выводы

Аэродинамические установки с открытой рабочей областью предполагают расширение ветрового потока, а значит, циркуляцию потоков в помещении и возникновение сторонних, искажающих измерения вихревых потоков. Результаты натурного эксперимента показали, что поток остается достаточно однородным по рабочей области, а скорости потоков за её пределами резко снижаются до нуля.

Для проведения компьютерного эксперимента необходимо точное соблюдение геометрических аспектов, как непосредственно применяемых моделей, так и изучаемых аэродинамических процессов, например, возникновения завихрений в ре-

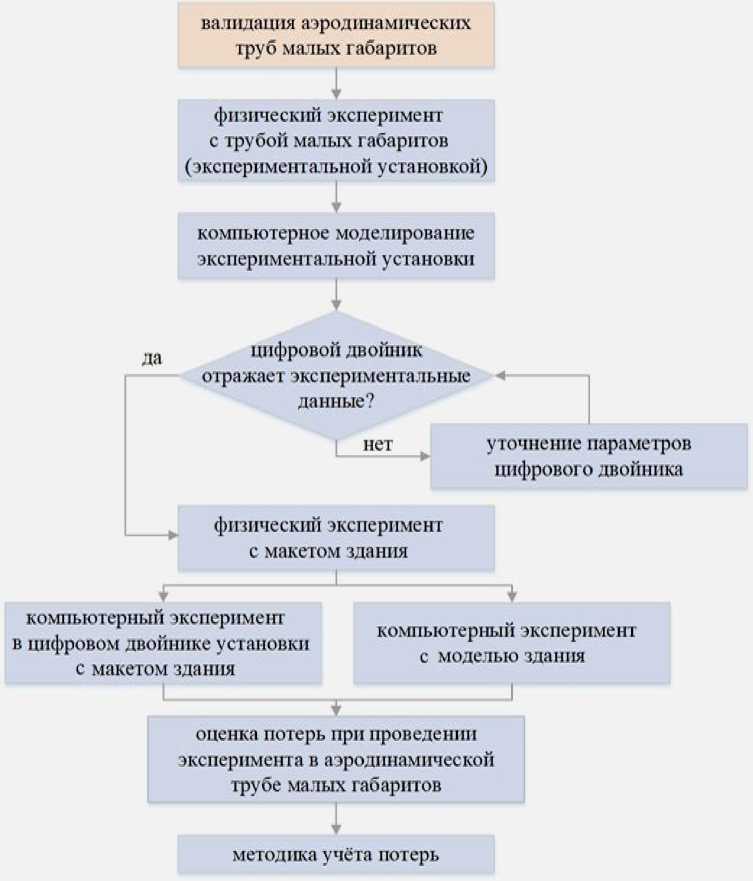
Рис. 8. Алгоритм цифровой поддержки в разработке методики валидации малогабаритных аэродинамических труб

зультате сложной геометрической формы. Создание точной цифровой копии аэродинамической установки при проведении компьютерного эксперимента позволило получить данные, подобные экспериментальным, визуализировать возникающие ветровые потоки и некоторые недостатки в работе труб малых габаритов.

Создание цифрового двойника аэродинамической установки позволило получить результаты, которые можно использовать при дальнейших проведениях экспериментов с установкой масштабных геометрических моделей в рабочей области аэродинамической трубы и создании их цифровых копий для виртуального прототипа в компьютерном эксперименте. Исследование дает возможность оценить качественно и количественно возникающие погрешности измерений, на основании которых могут быть введены поправочные расчетные коэффициенты и разработана методика их учета (см. рис. 8).