Алгоритм фильтрации запросов к ресурсоемким web-сервисам на основе алгебраических соотношений

ВВЕДЕНИЕ                                      Поскольку только управление запросами

Одним из важнейших требований к любой сетевой системе, ориентированной на предоставление информационных услуг широкому кругу пользователей, является обеспечение устойчивой бесперебойной работы, в том числе и в режимах нагрузки, близкой к предельным возможностям системы по количеству обрабатываемых запросов [2], [5]. Ситуации, когда система не справляется с обработкой поступающих запросов из-за недостатка имеющихся аппаратных ресурсов, будем называть перегрузкой. В частности, данная проблема актуальна для корпоративных информационных систем, построенных на базе интерактивных web-технологий, где функционал системы является отражением бизнес-функций предприятия.

Основные меры, направленные на предотвращение перегрузок, сводятся либо к наращиванию общей производительности системы [3], либо к управлению запросами, то есть к отклонению части из них на этапе поступления в систему в соответствии с некоторыми критериями. Надо отметить, что в силу специфики функционирования web-сервисов подходы, успешно применяемые при функционировании некоторых транспортных протоколов, например TCP [8], и основанные на обратной связи, позволяющей предотвратить перегрузку путем направления соответствующего сообщения отправляющему запросы клиенту, неприменимы, что вынуждает искать иные альтернативы.

позволяет предотвращать ситуации перегрузок даже при недостатке имеющихся вычислительных ресурсов, в рамках данной статьи сосредоточим внимание именно на этом методе.

В работах [4], [7] рассматривалось управление запросами к ресурсоемким web-сервисам (системам дистанционного обучения и сетевым системам моделирования). В частности, было предложено производить управление запросами путем отсечения части из них согласно долям, определенным соответствующими коэффициентами для каждого сетевого сервиса. Пересчет коэффициентов производится регулярно с периодичностью, позволяющей учесть изменения характеристик потока поступающих в систему запросов.

Несмотря на явные достоинства предложенных моделей управления запросами, они не лишены недостатков: при поиске параметров управления запросами необходимо всякий раз решать оптимизационную задачу, что при регулярном пересчете и большом количестве учитываемых факторов может стать ощутимой дополнительной нагрузкой на сервер и ограничивает как сферу применения предложенных моделей, так и возможности их развития.

Поэтому основными задачами исследования стали поиск возможностей для снижения вычислительной сложности рассмотренных схем управления запросами и повышение эффективности управления в ситуациях значительной флуктуации интенсивности поступающих запросов.

ИЗМЕНЕНИЕ ПАРАМЕТРОВ УПРАВЛЕНИЯ

ЗАПРОСАМИ

В идеале параметры управления запросами должны в точности соответствовать характеристикам потока поступающих запросов, однако на практике такое соответствие поддерживать затруднительно: в общем случае предугадать поведение сетевого трафика крайне сложно, к тому же изменение параметров управления запросами требует учета большого количества влияющих факторов, что неизбежно сказывается на вычислительной сложности алгоритма.

В предложенных моделях в целях актуализации параметров управления их пересчет предлагается производить регулярно через интервал времени т, выбираемый индивидуально для каждой системы (см. рисунок). Фактически параметры управления запросами изменяются дискретно, в то время как параметры потока запросов - непрерывно.

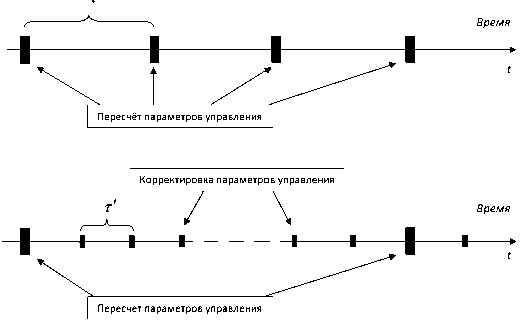
Моменты изменения параметров управления запросами

Учитывая, что пересчет является затратной с вычислительной точки зрения операцией, один из возможных путей развития данной схемы заключается в том, чтобы взамен полного пересчета осуществлять корректировку параметров через меньший интервал времени т'. Алгоритм корректировки должен позволять получать пусть и не строго оптимальный результат, но близкий к нему, при этом требуется гораздо меньше вычислительных ресурсов. Это позволит снизить нагрузку на сервер за счет увеличения временного интервала между полными пересчетами параметров управления без ущерба для их адекватности.

Достижение таких требований возможно, если алгоритм будет учитывать лишь наиболее значимые факторы при принятии решения об обслуживании.

УЧЕТ ТОЛЬКО ОДНОГО ВИДА РЕСУРСОВ

Возможности системы по обработке всех поступающих запросов определяются количеством имеющихся доступных вычислительных ресурсов. В информационных системах в роли таких ресурсов, как правило, выступают производи- тельность процессора, доступный объем оперативной памяти, пропускная способность линий связи, доступный объем дисковой памяти и т. д.

На практике перегрузка обычно возникает вследствие недостатка ресурсов только одного-двух видов, в то время как остальные не востребованы полностью. Поэтому в ряде случаев можно говорить о наличии в системе наиболее востребованного ресурса, запасы которого будут истощены в первую очередь. При наличии в системе такого ресурса его достаточность фактически будет определять предел общей производительности системы, а ограничениями на объем остальных можно пренебречь.

Пусть в системе имеется множество сетевых сервисов M (I Е M) и множество видов вычислительных ресурсов K (j Е K ) . Будем считать известными интенсивности потоков запросов к сервисам X и потребности сервисов в ресурсах каждого вида S j . Доступное количество имеющихся в системе ресурсов каждого вида ограничим соответствующим значением V^j .

Введем в рассмотрение степень востребованности j -го ресурса W , представляющую собой отношение необходимого количества данного ресурса для обслуживания всего потока запросов к его доступному количеству в системе.

У А "У

w* =   j Е K

Если w ^j < 1, можно говорить о том, что данный ресурс не израсходуется полностью и не может стать причиной перегрузки, а потому не влияет на принятие решения об отклонении запросов. Если w ^j > 1, доступного количества данного ресурса недостаточно для обслуживания всех поступающих запросов, что должно быть учтено при определении параметров управления.

Чем больше степень востребованности wj, тем в большей мере ресурс j ограничивает возможности системы по обработке запросов. Таким образом, выбор наиболее востребованного ресурса может происходить по формуле wq = max{ wj | wj > 1}.

Поскольку потребность в ресурсах различных видов для работы разных сервисов различна, а управление запросами не всегда предполагает пропорциональное сокращение трафика ко всем сервисам, приведенная формула должна быть усилена в части выполнения ограничений по имеющимся объемам для ресурсов всех видов.

В наиболее общем случае достаточно, чтобы значение wq наиболее востребованного ресурса значительно превышало значения потребности в ресурсах других видов.

w q = max{ w j | w j >  1}

<

w q >>  max{ w j }

j e K

J e K \ q

Таким образом, при соблюдении ряда условий число ограничений на количество доступных вычислительных ресурсов в модели может быть сокращено за счет исключения тех из них, которые не влияют на итоговый результат.

СПОСОБ КОРРЕКТИРОВКИ БЕЗ РЕШЕНИЯ ЗАДАЧИ ОПТИМИЗАЦИИ

Рассмотрим способ поиска параметров управления запросами, основанный на отказе от формулирования задачи математического программирования. Для предотвращения заторов при передаче дейтаграмм в IP-сетях успешно применяется метод взвешенной максиминной схемы равномерного распределения ресурсов [1]. Ниже представлена адаптация данного алгоритма применительно к управлению запросами к web-сервисам. Будем исходить из того, что в системе имеется лишь один ресурс, количество которого определяет ее возможности по обработке запросов.

Введем основные обозначения модели. Пусть в системе имеется множество сетевых сервисов M (i G M). Будем считать известными интенсивности потоков запросов без^управления к сервисам на предыдущем X = { X ,..., X n } и текущем X = { X 1 ,..., X n } этапах определения (корректировки) параметров управления. Общий объем разделяемого ресурса ограничим значением V. Через S. обозначим объем ресурса, необходимый для выполнения сервиса i.

Результатом работы алгоритма будем считать определение компонент вектора Ц = {ц1,...,Цп} как максимально возможные интенсивности за- просов к соответствующим сетевым сервисам, не вызывающим перегрузки. Зная Ц = {/4,—,Цп} и X = {X,,..., Xn}, легко найти коэффициенты, определяющие долю запросов, которые необходи- мо отклонить для предотвращения перегрузки.

Будем считать, что определенный для каждого сетевого сервиса приоритет P. влияет на определение доли ресурса. Объем ресурса V , гарантированно доступный для i -го сервиса, может быть найден по формуле

Р

V = V ^{P i} = V ⋅ P

£ P k      .

k ∈ M

Дополнительно в модели делается допущение, что объемы имеющихся вычислительных ресурсов являются постоянными величинами. Данный подход не вполне соответствует реальным системам, где эти величины зависят от многих факторов [6]. К тому же при одновременном выполнении нескольких запросов общий требуемый объем ресурсов не всегда может быть представлен в виде алгебраических сумм потребностей каждого запроса в отдельности.

Из-за указанных допущений результат работы алгоритма не является строго оптималь- ным, что особенно может проявиться в случаях, когда количество активных сервисов невелико, а характеристики потока запросов подвержены значительным флуктуациям. Это позволяет рассматривать предложенный способ как пригодный только для корректировки имеющихся параметров управления, а их расчет должен производиться по другим схемам.

Для начала рассмотрим систему, в которую поступают запросы только к одному сервису. Интенсивность потока с управлением ц либо совпадает с интенсивностью входного потока без управления X , если имеющихся ресурсов достаточно для обслуживания всех поступающих запросов, либо ограничена имеющимися возможностями системы. Зависимость между X и ц можно представить в виде

X = Ц } ц = Ц

V

Ц 1 = min ^{— , Л ^}.

⁵ 1

Рассмотрим систему, в которой функционируют два сервиса. Интенсивность потока запросов с управлением к сервису в этом случае ограничена либо интенсивностью потока запросов без управления X , либо гарантированно выделяемым этому сервису объемом ресурса V в совокупности с объемом ресурса, незадействованно-го вторым сервисом, если тот не использует свой лимит полностью.

X = Ц , X }      ц = { Ц 1 , ц ₂}

,V. V - min{ 5 X , V }„

Ц 1 = min{ X 1,max{ V -, { ^{X 2}} }}, ⁵ 1             ⁵ 1

. ..      .V V - min{ 5,X , V }_н

Ц = min X , max { 5- 5    ° }}.

Поскольку при работе 2 ресурсов V = V 1 + V ₂, справедливо неравенство

V - min{ 5 2X2, V>} = V1 + V> - min{ 5 2 X V2} - V, а форму- лы могут быть приведены к виду

P

V - min { 5, X , V ²—}

• .    .. V - min{ 5₂ X , V ₂ L ■                      P + P .

Ц = mm^,------ 2 2 2J} = mm^,----------

P

V - min { 5. X , V ¹—}

• .     V - min{ 5. X , V .}.     .              ¹¹¹ p + P₂\

Ц2 = min{X,,--------{ ' 4 , ' }} = mm{X2,-------------

Рассмотрим систему, в которой запросы поступают к нескольким сервисам. Для начала разделим все имеющиеся сервисы на два множества:

• 1)    м ДОСТ = ! { _г1 5 ,. X, < V , } i е M , (1) если сервису достаточно предоставляемого гарантированного объема ресурсов V_i для обслуживания потока запросов X_i в полном объеме ( X . = ц . ). В таком случае объем предоставляемых сервису ресурсов может быть сокращен до необходимого значения (произведения интенсивнос-

• ти входящего потока λi и сложности выполнения этого одного запроса Si ).

• 2)    M НЕДОСТ = {i I S i • A i >  V i } i e M , если сервису недостаточно предоставляемого гарантированного объема ресурсов V_i для обслуживания потока запросов λ_i в полном объеме.

Учитывая, что сервисы из множества M^ДОСТ не используют полностью предоставляемые им вычислительные ресурсы, образующиеся резервы могут быть перераспределены в пользу сервисов из множества M^НЕДОСТ . Найдем объем невостребованных сервисами из множества M^ДОСТ резервов V^СВОБ через разность между гарантированно предоставляемыми объемами ресурса и фактическим его использованием:

VСВОБ = Z jSj.Aj) = V- Z Si"Aj- Z  Vj j eM ДОСТ                         jeM ДОСТ            jeM НЕДОСТ

= V - Z min{ S ,' A J , V j } = V - Z min{ ^S j" A j , V - P j } .

. i e M                             j e M

Полученный объем разделим между нуждающимися сервисами i ∈ M^НЕДОСТ согласно принципам приоритетов. Тогда объем дополнительно выделяемых ресурсов для каждого конкретного сервиса V_i^ДОП ( i ∈ M^НЕДОСТ ) может быть найден по формуле:

V i ДОП = V СВОЕ --J i ----= I V - Z min{ S j ■ Aj , V ■ P j } I-- =P----

Z  Pk  V   jeM              ) Z  Pk k eM НЕДОСТ                                           k eM НЕДОСТ i e MНЕДОСТ .

В результате для сервисов из множества M^ДОСТ интенсивность потока μ_i будет определяться интенсивностью потока λ_i , а для сервисов из множества M^НЕДОСТ – отношением объема предоставляемых ресурсов (гарантированно предоставляемый объем V_i и дополнительно выделяемый из неиспользуемых резервов объем V_i^ДОП ) к сложности выполнения запросов S_i . Итоговая формула примет вид:

A = { A , A 2 ,..., A n }         ^ = { ц _х, ц _г,.„, H n }

V + у^ДОП

Н, = min{Ai,      ----} = ri                          ) p (3)

V ■ P i +1 V - Z min{ S j. A j , V ■ P j } I- i V    j e M                ) Z ^Pk

.                                                           k e M НЕДОСТ ,

= min{ A i ,------------------------------------------------- } .

Коэффициент, отражающий долю запросов, которые необходимо пропустить для выполнения к конкретному сервису, может быть легко найден через соотношение:

H i

x = 1 ^A i

A i >  0

A i = 0

Алгоритм управления запросами:

Шаг 1. Определение необходимости в управлении запросами

Оценивается разница VНЕДОСТ между общим количеством имеющегося ресурса и фактической потребностью в нем для обслуживания всех поступающих в систему запросов.

V ^недост = Z A i. S i

i e M

- V

В зависимости от значения:

1) Если V^НЕДОСТ <  0 ^ H i = 1

V i e M ,

име-

ющегося в системе объема вычислительного ресурса достаточно для выполнения всех поступающих запросов, управление запросами не требуется. Работа алгоритма прекращается.

• 2)    Если V^НЕДОСТ> 0, имеющегося в системе объема вычислительного ресурса недостаточно для выполнения всех поступающих запросов, требуется фильтрация части запросов (переход к шагу 2).

Шаг 2. Определение необходимости в корректировке

Определяется необходимость корректировки существующих параметров управления запросами исходя из изменения характеристик потока запросов. Составляется перечень сервисов, интенсивность запросов к которым существенно не изменилась. Введем поправочный коэффициент ω > 0 для устранения незначительных флуктуаций параметров трафика.

M неизм = U { i |(1 - го ) ■ A i <  A i < (1 + ^ ) ■ A i } i e M .

Если M^неизм = М , можно говорить о том, что характеристики потока запросов изменились незначительно, а существующие параметры управления запросами не нуждаются в корректировке. В остальных случаях необходима корректировка (переход к шагу 3).

Шаг 3. Корректировка параметров управления запросами

Производится определение параметров управления запросами в зависимости от сложности их выполнения, уровня приоритета и интенсивности поступления.

• 1)    По формуле (1) определяется перечень сетевых сервисов, интенсивность запросов к которым не превышает выделенные для них квоты.

• 2)    По формуле (2) определяются объемы дополнительно распределяемого ресурса для каждого сетевого сервиса.

• 3)    По результатам полученных значений с использованием соотношения (3) на основе имеющейся информации об интенсивности запросов к каждому сервису определяется доля запросов, которые должны быть отклонены с целью предотвращения возникновения перегрузки.

Шаг 4. Фильтрация трафика

На основе полученных коэффициентов и длительности периода управления запросами определяется предельное число запросов для каждого сетевого сервиса. Запросы, превышающие установленные квоты, отклоняются.

ЗАКЛЮЧЕНИЕ

Предложенный алгоритм позволяет упростить процесс управления запросами по сравнению с ранее предлагаемыми моделями за счет учета лишь наиболее значимых факторов, а также дает возможность более оперативно реагировать на изменение характеристик потока поступающих запросов. Управление запросами может дать положительный эффект, однако результат во многом зависит от динамики изменения характеристик потока запросов и правильности выбора критериев управления.

На наш взгляд, развитие подобных алгоритмов должно следовать по пути уменьшения вычислительной сложности при обеспечении достаточной эффективности управления запросами. Вопросы применимости в реальных системах, оценки эффективности предложенных моделей являются темой дальнейших исследований и оставлены за рамками данной статьи.

В заключение стоит отметить, что управление запросами не является полноценным восполнением недостающих вычислительных способностей системы, хотя и позволяет системе с минимальными потерями преодолевать ситуации, когда возможность качественного оказания информационной услуги наиболее уязвима. Гарантированное обслуживание подразумевает наращивание вычислительных ресурсов сервера и/или уменьшение сложности выполнения запросов.