Алгоритм формирования сигналоподобных помех с использованием адаптивных фильтров

О дним из способов надежной защиты информации, которая циркулирует в выделенном помещении, является постановка помех, затрудняющих прием и расшифровку полезного сигнала. В этом случае широко используются различные генераторы шумовых помех, которые маскируют сигнал, затрудняя возможность у противника его обнаружения и выделения в приемном устройстве. При этом в условиях априорной неопределенности относительно параметров сигнала зачастую используются генераторы шума, излучающие помеховый сигнал достаточно высокой мощности и широкой частотной полосы.

В этой связи актуальной представляется разработка алгоритма формирования сигналоподобной помехи, которая могла бы генерировать помеху с минимально возможной мощностью и амплитудно-частотной характеристикой, повторяющей спектр сигнала.

Алгоритм формирования сигналоподобной помехи

В основе синтеза алгоритма формирования сигналоподобной помехи (рис. 1) лежит схема классического винеровс- кого фильтра. Основным отличием представленного алгоритма формирования сигналоподобной помехи является принудительное «примешивание» белого шума к полезному сигналу. В свою очередь, формирующий белый шум в смеси возбуждает N-мерное пространство весовых коэффициентов [1], а адаптивный фильтр 1 настраивается таким образом, чтобы его выходной сигнал соответствовал исходному процессу по критерию наилучшего среднеквадратического приближения.

В результате импульсная характеристика адаптивного фильтра 1 будет стремиться к соответствию с полезным сигналом. Передаточная функция адаптивного фильтра 1 в установившемся режиме согласно [2] определяется как:

км =

sxn sxwsM

где S_x(ω) – спектральная плотность полезного сигнала, S_υ(ω) – спектральная плотность формирующего белого шума.

Для того чтобы сформировать сигналоподобную помеху необходимо переписать весовые коэффициенты в адап-

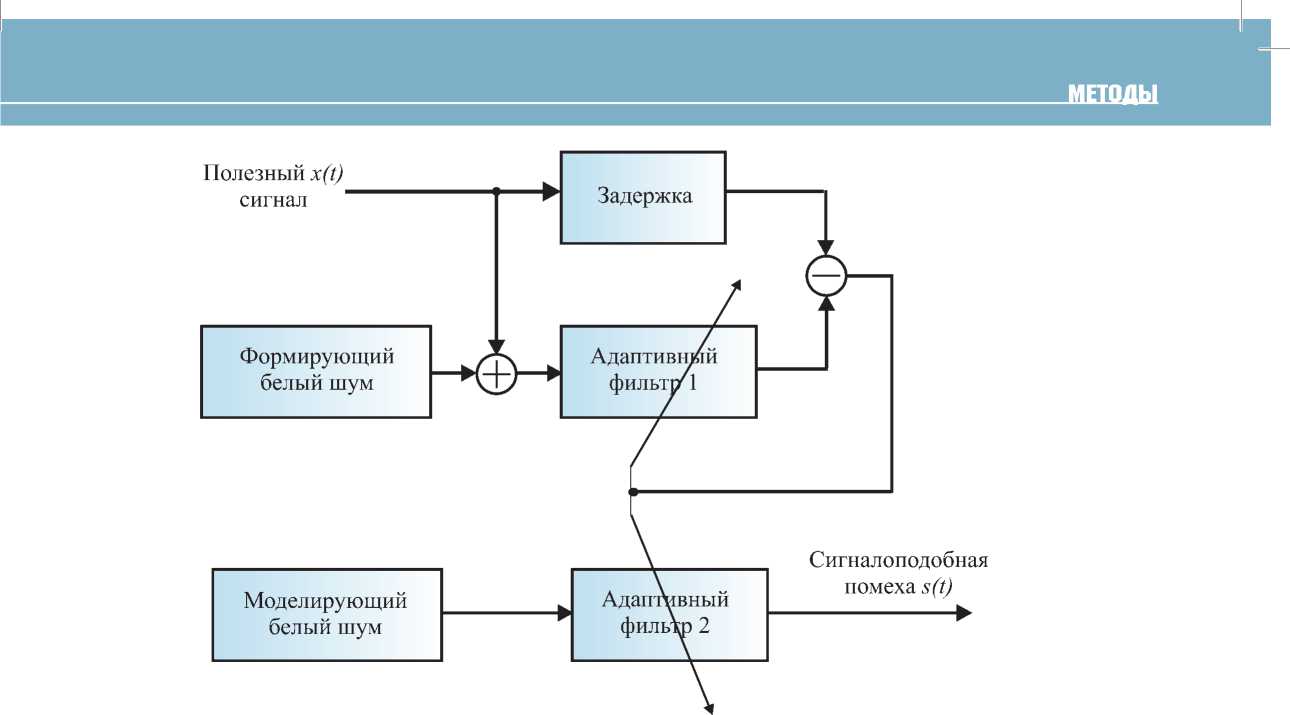
Рис. 1. Структурная схема формирователя сигналоподобной помехи

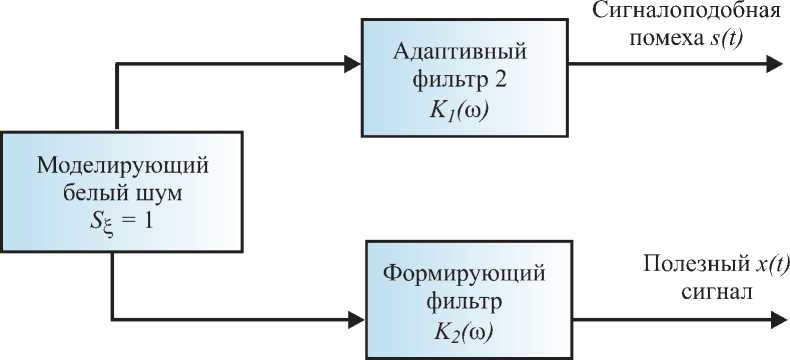
Рис. 2. Структурная схема устройства оценки адекватности модели

тивный фильтр 2, на входе которого действует «белый шум». Таким образом, на выходе такого адаптивного фильтра 2 генерируется сигналоподобная помеха, которая по сути является адаптивной моделью сигнала [3].

Определенный выбор задержки позволяет несколько снизить дисперсию ошибки моделирования сигналоподобной помехи. В [2] задержку рекомендуется выбирать равной половине длины адаптивного фильтра.

Для оценки адекватности (или качества) формируемой модели полезного сигнала [4] проведем оценку среднеквадратического отклонения временной реализации сигналоподобной помехи от временной реализации полезного сигнала в соответствии со схемой на рис. 2 .

Численно адекватность модели можно оценить по нормированному среднему квадрату ошибки:

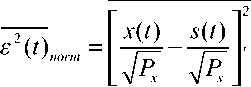
где x(t) – временная реализация оценки полезного сигнала, s(t) – временная реализация сигналоподобной помехи, P_s – мощность сигналоподобной помехи, P_x – мощность полезного сигнала.

Перейдем в формуле (2) к спектральным плотностям и получим:

f2(0

v /norm

з s(tMt)

7^7^"

= 2

-2   ----- ----- s(f) X^ _S2(t) X2(t) .

s

1--Д r-

р

×

^2a J

—7---dco cl' + co'

j S^K_x , (3)

где R_sx – взаимная корреляционная функция сигналоподобной помехи и полезного сигнала, К₂(jω) – ко эффициент передачи формирующего фильтра, S_ξ – спектральная плотность мощности моделирующего белого шума.

Учитывая, что для стационарных входных сигналов спектральные плотности S_x(ω) и S_υ(ω) , входящее в выражение (1), есть неотрицательные и вещественные функции [5], то коэффициент передачи адаптивного фильтра также является неотрицательным и вещественным. Тогда коэффициент передачи формирующего фильтра K₂(jω) можно принять равной квадратному корню из отношения спектральной плотности полезного сигнала к спектральной плотности моделирующего белого шума.

Поэтому, подставляя (1) в (3), окончательно находим

e\0 = 2 v / norm

×

--------Js (co)dco . s»+s>r

Пусть в качестве полезного сигнала выступает непрерывный гауссово-марковский процесс [6] со спектральной плотностью

^.(to)^

Аэ'2а a2 +co2

Тогда оптимальная передаточная функция адаптивного фильтра 1 представляется

KM =

2aq co2 +a2 +2aq

где q - отношение мощности марковского процесса и формирующего белого шума.

Подставляя спектральные плотности в выражение (4), получаем адекватность модели марковского процесса:

1     7 lag

.

Вначале найдем мощность модели марковского процесса:

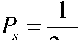
2n

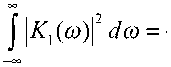
2aq co2 + a2 -v2aq

(agf

^2aq + a2y

Затем вычислим интеграл в выражении (7):

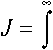
2aq co2 +a' +2aq

^2a j

^---dco = a' + co

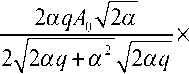
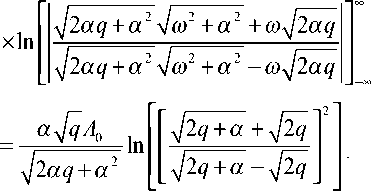
Подставляя выражения (8), (9) в (7) получаем:

е\Л =2 v /norm

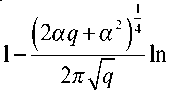
^2q + a + -^2^ ^2q + a -y/2q

Находим минимум выражения (10), продифференцировав

его по параметру q и приравняв полученное выражение к

нулю, a4

3                 5

2nq- {2q + aY

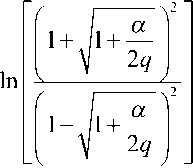
× ^q-va^^2q-va - %-j2q- -4a^2q

Jl ^^. ^-^^1    ^.

Решая полученное выражение численными методами, определяем оптимальное отношение сигнал-шум q , при котором модель сигнала наиболее адекватна:

qonm-2,%6a =2^6-271^- где Δf – ширина полосы сигнала в Гц, fs – частота дискретизации в Гц.

Таким образом, оптимальным параметром формирования адаптивной модели полезного сигнала является отношение мощности полезного сигнала и формирующего белого шума q ( рис. 3 ).

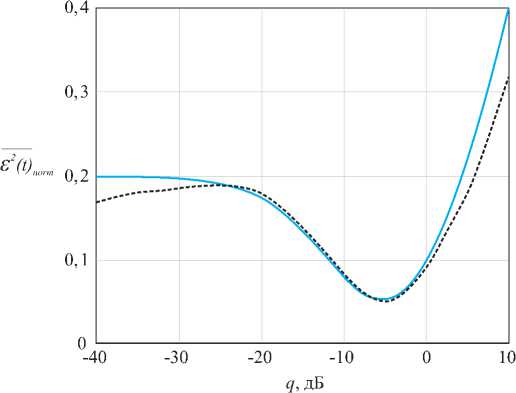
Рис. 3. Зависимость E (У) от q для марковского процесса при α = 0,1: теоретическая (сплошная) и моделируемая (пунктирная)

Компьютерное моделирование

Для оценки маскирующих свойств сигналоподобной помехи, сформированной предложенным алгоритмом, использу- ется устройство формирования оценки дисперсии ошибки фильтрации (рис. 4). В него входит генератор помехи, декоррелятор в виде нерекурсивного фильтра, адаптивный автокомпенсатор помех (АКП) [2], устройство оценки дисперсии ошибки фильтрации.

С помощью двухканального адаптивного автокомпенсатора и устройства оценки дисперсии ошибки фильтрации оценивается возможность обнаружения и выделения полезного сигнала (марковского процесса) при использовании в качестве помехи белого шума, марковского процесса, а также адаптивной модели марковского процесса.

Устройство формирования оценки ошибки позволяет моделировать работу адаптивного автокомпенсатора как в условиях действия коррелированных помех на обоих входах компенсатора, так и при их частичной (или полной) декорреляции. Декорреляция помех осуществляется декоррелятором, выполненным в виде нерекурсивного фильтра. Декоррелятор функционально необходим для создания условий, приближенных к реальной работе автокомпенсаторов. На вход устройства формирования оценки дисперсии ошибки фильтрации подается сигнал, к которому примешивается сформированная помеха. Смесь поступает на один вход автокомпенсаторов, а на другой помеха, частично декоррелиро-ванная с помехой в основном канале. По дисперсии ошибки проводится оценка работы автокомпенсаторов. Для удобства представления дисперсия ошибки определяется как где δ12 – нормированное к мощности полезного сигнала среднеквадратическое отклонение полезного сигнала от его оценки на выходе АКП.

С помощью разработанного программного обеспечения «Система адаптивной постановки помех» были получены зависимости дисперсии ошибки фильтрации полезного сигнала от отношения мощности сигнал-помеха, когда в качестве полезного сообщения использовался гауссово-марковский процесс, в качестве помехи - белый шум, гауссово-марковский процесс и адаптивная сигналоподобная помеха с разными коэффициентами взаимной корреляции помех в каналах ( r ).

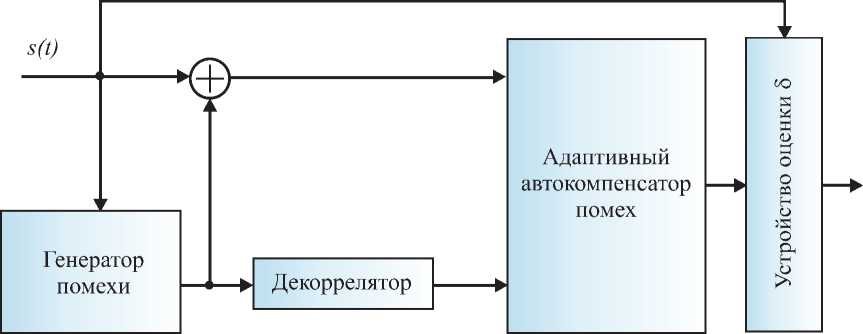
Рис. 4. Структурная схема устройства формирования оценки дисперсии ошибки фильтрации

Параметры моделирования отображены в табл. 1 , параметры сигнала и помех – в табл. 2 . Результаты моделирования изображены на рис. 5–8 . Измерение мощности сигнала и помех проводились в полосе Найквиста.

Таблица 1. Параметры моделирования

Параметр	Значение
Частота дискретизации ( fS ), Гц	200000
Объем выборки для оценки δ2	65536
Количество выборок для усреднения δ2	10
Число весовых коэффициентов АКП	2048
Коэффициент адаптации АКП	0,01
Алгоритм адаптации АКП	метод наименьших квадратов [2]

П, дБ

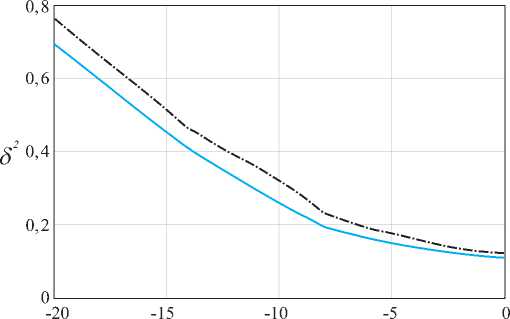
Рис. 6. Зависимость нормированной дисперсии ошибки фильтрации от отношения мощности сигнал-помеха в условиях действия адаптивной помехи (сплошная) и марковской помехи (штрихпунктирная) при коэффициенте взаимной корреляции помех r = 0,99

Таблица 2. Параметры сообщения и помех

Тип	Параметры
Марковский процесс	ширина полосы = 3354 Гц
Адаптивная помеха	длина адаптивной модели L = 128 ; коэффициент адаптации M = 0,01; отношение с/ш qопт = -5дБ; алгоритм адаптации – метод наименьших квадратов [2]

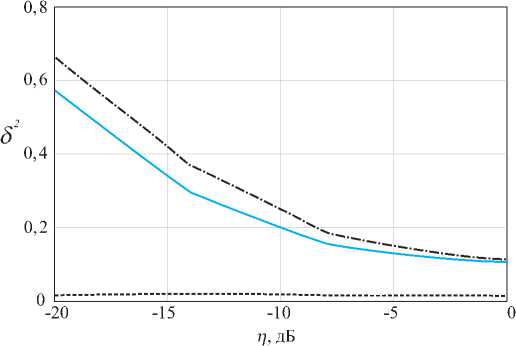
Рис. 5. Зависимость нормированной дисперсии ошибки фильтрации от отношения мощности сигнал-помеха в условиях действия адаптивной помехи (сплошная), марковской помехи (штрихпунктирная) и белого шума (пунктирная) при коэффициенте взаимной корреляции помех r = 1

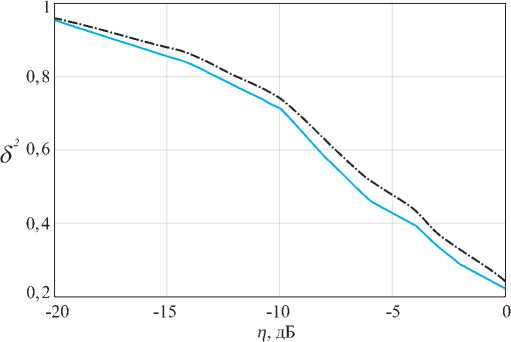
Рис. 7. Зависимость нормированной дисперсии ошибки фильтрации от отношения мощности сигнал-помеха в условиях действия адаптивной помехи (сплошная) и марковской помехи (штрихпунктирная) при коэффициенте взаимной корреляции помех r = 0,88

Анализ рис. 5 - 8 свидетельствует о высокой эффективности постановки адаптивной помехи, сформированной на основе алгоритма формирования адаптивных моделей случайных процессов. Данный алгоритм позволяет сформировать сигналоподобную помеху, по спектральной плотности мощности совпадающей с сигналом и с минимально возможной мощностью помехи.

Алгоритм формирования адаптивной модели полезного сигнала позволяет получать сигналоподобную помеху по эффективности значительно выше, чем широкополосный шум и при небольшом проигрыше марковской помехе. В частности, при единичном коэффициенте корреляции помех в каналах и отношении мощности сигнал-помеха рав-

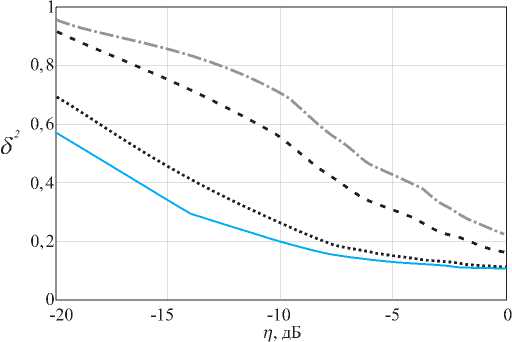
Рис. 8. Зависимость нормированной дисперсии ошибки фильтрации от отношения мощности сигнал-помеха в условиях действия адаптивной помехи при коэффициенте взаимной корреляции помех r = 1 (сплошная), r = 0,99 (точечная), r = 0,95 (пунктирная), r = 0,88 (штрихпунктирная)

ном -15дБ, дисперсия ошибки фильтрации для белого шума составляет 0,02, для марковской помехи – 0,42, тогда как для сигналоподобной помехи – 0,35, что позволяет сигналоподобной помехой «накрывать» полезный сигнал при меньших ее уровнях по сравнению с широкополосной помехой.

Чтобы обеспечить дисперсию ошибки фильтрации 0,4 при использовании сигналоподобной помехи экономия мощности по сравнению с белым шумом составляет более 20 дБ, а проигрыш марковской помехе составляет всего 3 дБ