Алгоритм форсирования режимов ударных испытаний, сформированных по данным натурных измерений

АЛГОРИТМ ФОРСИРОВАНИЯ РЕЖИМОВ УДАРНЫХ ИСПЫТАНИЙ, СФОРМИРОВАННЫХ ПО ДАННЫМ НАТУРНЫХ ИЗМЕРЕНИЙ1

Рассматривается форсирование режимов ударных испытаний, сформированных по результатам натурных измерений, на примере воздействий, возникающих при авиационном транспортировании космических аппаратов самолетами Ил-76. Форсирование проводится относительно максимальных значений уровнейударны.х спектров ускорений, зарегистрированных при натурном транспортировании.

Для анализа нагружения космического аппарата (КА) при авиационном транспортировании используются алгоритмы разделения воздействий на стационарные и нестационарные составляющие [1; 2].

Нестационарные воздействия, полученные после разделения исходного процесса на стационарные и нестационарные составляющие, включают в себя общее количество воздействий для всех случаев реализации (количество случаев транспортирования), а для того чтобы проводить испытания, необходимо выделить время действия нагрузки на конкретных режимах из условий дальности полета и количества взлетов и посадок.

Следует отметить, что нагрузки с максимальными амплитудами действуют на самолет только незначительную часть всего временного интервала, соответствующего конкретному режиму транспортирования. Кроме того, часть нагрузок, соответствующая, например, крейсерскому полету, не представляет опасности для сохранности транспортируемого груза ввиду их малости, а только увеличивает время загрузки испытательного оборудования при отработке таких режимов.

То есть процедура получения нагрузок по результатам обработки данных о натурном транспортировании [1], давая реальные нагрузки (спектральные плотности мощности виброускорений и величины ударных спект ров ускорений) для формирования режимов вибрационных и ударных испытаний, не решает проблему их оптимального проведения.

При формировании режимов отработочных испытаний на случай авиационного транспортирования таких специальных грузов, как КА, необходимо учитывать следующие параметры: условия транспортирования (тип самолета, его загруженность, типы аэродромов взлета и посадки, погодные условия и т. д.), дальность транспортирования, количество взлетов и посадок за время транспортирования. Если условия транспортирования определяют, в первую очередь, амплитудные величины нагрузок, то дальность транспортирования и количество взлетов и посадок определяют время воздействия этих нагрузок. Создание оптимальных режимов отработки грузов представляет собой нетривиальную задачу С одной стороны испытания на повышенных режимах могут привести к отказу КА, а с другой - стоимость часа работы испытательного центра очень велика, так как приходится использовать уникальное оборудование. Поэтому испытания на режимах, не представляющих опасности для КА, необходимо обоснованно сокращать, заменяя их эквивалентными испытаниями на более жестких режимах нагружения.

Наиболее распространенным на сегодняшний день является подход к формированию эквивалентных режи- мов испытаний, основанный на гипотезе линейного/не-линейного суммирования (накопления) повреждений [3].

Как известно, уравнение кривой усталости наиболее часто записывается в виде [4]

о m N = A = const ^,

где т - показатель наклона кривой усталости материала исследуемой конструкции; о - напряжение в материале; У - число циклов перемен напряжений в материале до разрушения.

Очевидно, что путем простых преобразований можно получить следующую формулу:

m = lg N 2 — lg N 1 , lg O i - lg O 2 где т - показатель наклона кривой усталости материала исследуемой конструкции;^ и У₂ - число циклов до разрушения материала при уровне напряжений о ₁ и о ₂ соответственно.

Тогда время испытаний Т_р можно связать со временем транспортирования T_t на основе гипотезы суммирования повреждений через коэффициент пропорциональности К и показатель наклона кривой усталости материала т :

T p = K^mT_t .

Так как при выводе формул используется гипотеза линейных повреждений, то, очевидно, что коэффициент К для ударного спектра ускорений равен

S

K =     ,

S _max так как ударный спектр ускорений функция линейная по g . Рассмотрим теперь следующий алгоритм формирования режимов испытаний. Полученный по результатам натурных измерений для каждой точки контроля транспортируемого груза псевдоисходный процесс с длительностью, равной общей длительности всех измерений, разделяем на стационарную и нестационарные составляющие.

Максимальные значения ударных спектров ускорений (УСУ) получаем по методу огибающих по данным обо всех случаях авиационного транспортирования для всех заранее определенных амплитудных диапазонов, а количество ударов определяем по формуле q=a

^NP =    £ ( ^S _h / ^S  ) N jq } ,

M t j =1 q =1

где N_p - количество ударов при испытаниях; У - количество ударов нау-ом режиме транспортирования в д-ом амплитудном диапазоне (общее количество ударов за время транспортирования N = ^У ); 5 . - текущее значение ударного спектра ускорений при транспортировании в амплитудном диапазоне; 5 - максимальное значение ударного спектра ускорений, полученное при транспортировании; М - необходимое количество взлетов и посадок; М - количество взлетов и посадок, для которых был сформирован режим ударных испытаний; в - коэффициент эквивалентности ударных испытаний; а - количество амплитудных диапазонов; п - количество режимов транспортирования.

Количество ударов форсируется относительно максимальному значению УСУ. Кроме того, при определении количества ударов максимальные значения ударно-

I -

го спектра ускорений, полученные по методу огибающих для всех амплитудных диапазонов по данным обо всех случаях авиационного транспортирования, заменяем ударными спектрами ускорений от их импульсов. Такие УСУ должны отличаться от огибающих УСУ на величину меньшую, чем погрешность определения ударных спектров ускорений.

Проведение испытаний по методу ударных спектров ускорений приводит к замене временной зависимости ее частотным представлением, так как при таких испытаниях не важен вид воздействия, а важна вызванная этим воздействием реакция объекта испытаний. Так как у одного и того же УСУ может быть бесконечное множество временных реализаций, то его воспроизведение возможно воздействиями, не отражающими физику реального нагружения. Чтобы этого избежать, необходимо формировать режимы испытаний с учетом частотных составляющих как внешнего воздействия, так и объекта испытаний.

Для замены ударных спектров ускорений одиночными импульсами воспользуемся подходом, предложенным в работе [5], где при формировании ударного импульса предлагается использовать частоты, на которых переносится основная энергия ударного воздействия. При совпадении частот воздействия и собственных частот конструкции возникают резонансы. Очевидно, что эти частоты всегда будут переносить основную часть энергии ударного воздействия, т. е. достаточно формальная характеристика (УСУ) дополняется содержащим физический смысл набором частот.

Будем искать внешнее воздействие в классе функций вида

m

* ( t ) = Z Ae

-

^a i t sin( to i t + ф i ) ,

где T( t) - ударный импульс ускорения; Ai -амплитуда ускорения при i частоте; ®i = 2пf - круговая частота колебаний;,/?-собственная частота колебаний; фi - фазовый сдвиг; ai = ^^, 8i = ln Zi, 8i - логарифмичес-π кий декремент колебаний; Zi - коэффициент затухания; i - номер текущей частоты; т - количество частот; t -время действия ударного импульса.

Это объясняется, в первую очередь, реальным набором сигналов, воспроизводимых системами управления электродинамическими стендами, которые наиболее часто применяются при вибрационных и ударных испытаниях.

После выделения массива частот to ? (а эта процедура плохо формализуется и требует определенного опыта) можно построить различные достаточно легко формализуемые алгоритмы получения необходимого воздействия.

Рассмотрим один из них, основанный на методе коллокации [6], в котором требуется обеспечить совпадение эталонного сигнала (ударного спектра v * ( to ) ) с ударным спектром от воздействия (ударного импульса)Л(t) только в заданном наборе точек to k ,( k = 1, 2,..., N ) .

Пусть имеется некоторый набор воздействий A m ( t ), m = 1,2,..., M , равный

M

^{A (} t ) = Z ^a m^Am ⁽ t ) .

m =1

Для каждого из воздействий строится свой ударный спектр, например, с использованием алгоритма, предложенного в работе [7]. Таким образом, получается зави симость ускорения от частоты, имеющая вид

^v ( ® ) = mах \а„ ⁽ t , ю )|.

Получаем нелинейную систему уравнений

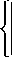
Е “ m a m ⁽ t , ® k )

m

= ^v ’ ⁽ ® k ) ,

гдек = 1, ...,М.

Решить данную систему можно итерационным способом. Для каждого воздействия А_дД) определяем дискретную последовательность я_т.( щ _к), где i - параметр времени, to _k - частота в методе коллокаций. Для каждой частоты to , выбираем тах_; |я_т . ( ю _к)| получаем выражение вида

A m = ^mах М® k )|.

Начальное приближение вычисляем как решение системы вида

M

Z A km « 0, m = ^⁽® k ), m =1

гдек = 1,2,..., m.

Система уравнений может быть вырожденной. В этом случае в качестве решения выбирается то решение, которое имеет наименьшее начальное | а ₀|. Если система несовместна, то от ряда уравнений можно отказаться, пожертвовав несколькими точками to _k в методе коллокаций. Дальнейшее построение итерационной последовательности а ₀, а ₁, ., а . ведется следующим образом. По приближению а определяется номер точки во времени, в которой отклик резонатора с частотой to _k достигает своего пикового значения при воздействии

M

A j ⁽ t ) = X “ j -, m A m ⁽ t ) .

m =1

Пусть этот номер будет Д, тогда определяем таблицу Aj,km = amД (®k )sign [^j,mamД (®k )] , по которой составляем систему линейных алгебраических уравнений

M

Z A jkkm ^a j + 1,m = ^VX ^ k ) m =1

для вычисления нового приближения а = 1. Сходимость итерационного процесса не является обязательной, поэтому целесообразно вести контроль последовательности а с целью выявления сходимости. В случае неудовлетворительной сходимости необходимо изменить выбор точек to_k на графике ударного спектра. Возможен вариант, в котором несколько различных наборов вектора а дают одинаковый или близкие друг другу ударные спектры. Итерационный процесс в этом случае может перескакивать с одного набора на другой. Это не является плохой сходимостью метода, а означает, что любое решение является приемлемым.

В качестве примера по рассмотренному алгоритму для этапа «взлет-посадка» выполнена замена ударных спектров ускорений, полученных при транспортировке космических аппаратов самолетами Ил-76, УСУ от одиночных импульсов по направлениям А', У, Z. Максималь ные значения УСУ-1 и аппроксимирующие их УСУ-2 от ударных импульсов: 3g sin (р/Зу + 6g sin(р/10)/ в направлении X, 6g sin(р/3)Z в направлении У, 9g sin(р/3)Z в направлении Z показаны на рис. 1-3.

Отличие полученных ударных спектров от экспериментальных не превышают погрешности измерений.

16-

-----СИзающопоматимуму — — — Норлироеанный УСУ

-■ 14

-. 12

14-

12-

10-

4-

2-

| 8'

6-

.„.а.   20 40 60 80 100 120 140 160 180200220240260280300

Частота, Гц

Рис. 1. Максимальный УСУ-1 по направлению Z и УСУ-2 его аппроксимирующий

0'

0 ’

10 20

50 аз 70 80 93 100 110 120 130 140 150 160 170 180 190 200 210 220 230 210 250 260 270 280 290 300 310

20 40 60 80 100 120 140 160 180 200220 240260 280300 Частота, Гц

7-

6-

• 5-

• 4-

К

2-

0-

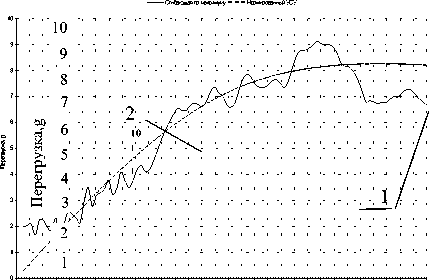
Рис. 2. Максимальный УСУ-1 по направлению У и УСУ-2 его аппроксимирующий

-----Сгибающая па максимуму---Нармироеанный УСУ

-11

" 10.

- 9V

6;,

3' "

1 "

0 10 20    0 ^П

50 ЯГ 70 80 90 100 110 120 130 140 150 160 170 180 100 200 210 220 230 240 25 260 270 280 200 300 310

20 40 60 80 100 120 140 160 180 200220 240260 280 300

Частота, Гц

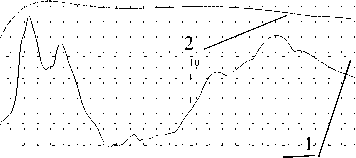
Рис. 3. Максимальный УСУ-1 по направлению^ и УСУ-2 его аппроксимирующий

Формирование испытательного воздействия, имеющего требуемый УСУ и включающий в себя частоты, несущие основную энергию ударного воздействия, позволит более качественно проводить данный вид испытаний.