Алгоритм функционирования имитационной модели процедуры калибровки инерциальной навигационной системы

В работе [1] выполнено математическое описание для процедуры калибровки инерциальной навигационной системы (ИНС) на движущемся объекте относительно вращающейся Земли. Следуя методу этой работы и использованным в ней обозначениям, но принимая основное допущение о том, что ИНС-А и ИНС-В функционально можно разделить на три подсистемы, каждая из которых представляет собой одноосную стабилизированную в инерциальном пространстве площадку и установленные на этой площадке два взаимно ортогональных акселерометра, расположенных в плоскости, перпендикулярной оси площадки, найдем решение задачи для одной такой подсистемы, т.е. частной задачи. Изменяя ориентацию оси площадки путем циклической перестановки, получим решение общей задачи для платформенных ИНС-А, ИНС-В.

. 1. Постановка задач

Платформенные эталонная ИНС-А и калибруемая ИНС-В установлены на объекте так, что начала связанных с ними системы координат (СК) совпадают с заданными точками О_А, О_в объекта (рис. 1).

Рис. 1. Расположение на объекте ИНС-А и ИНС-В

Модели погрешностей площадки и акселерометров ИНС-В имеют вид:

^ = pg+pQ_a®+pQ_a®;             (1)

А^-^+^-ь^,         (2)

где а® - проекции вектора кажущегося ускорения в СК Z® связанной с площадкой ИНС-В; Р^, Ру , z = 1, 2; у = 0, 2 - подлежащие определению калибровочные коэффициенты (КК), являющиеся постоянными.

Движение объекта в плоскости O_zZ_xZ₂, связанной с Землей СК, задано функциями:

q(f) = а^е sin coz, te [Z_o, Г];                   (3)

W;(t) = a_i2t² + a,y, z = 1, 2; Ze[Z_o, T],      (4)

где q - угол поворота вокруг оси Z₃, перпендикулярной плоскости движения, W, - проекции вектора ускорения точки Оу - объекта на оси СК Z.

Задача заключается в разработке:

• •    имитационной модели (ИМ) для процедуры определения КК площадки и акселерометров ИНС-В и составлении алгоритма функционирования этой ИМ;

• •    алгоритма определения КК для ИНС-В на основе заданной априорной информации о величине гравитационного ускорения, измерений: сигналов датчиков углов ИНС-А Q^A = q, ИНС-В Q®, сигналов акселерометров ИНС-А А^а = а_х, сигналов акселерометров ИНС-В А®.

Поставленные задачи будем решать при допущениях:

• •    не учитываем вращение Земли;

• •    гравитационное поле в объеме объекта является одинаковым во всех его точках.

• 2.    Математическое описание для решения поставленных задач

Модель погрешности площадки (1) представляет собой дрейф (уход) площадки от идеальной стабилизации в горизонтальной плоскости, определяемой площадкой ИНС-А, а поэтому на основе Аб необходимо определить Аб. А так как количество неизвестных КК площадки ИНС-В равно трем, то нужно иметь величины Аб, определенные для трех разных моментов времени, и для определения КК площадки следует использовать систему уравнений

- ^ + Р?«п + Р?а®1 = Аб₂;             (5)

pQ+pQa®3+p2a®3=^3.

В рассматриваемой задаче принято А0 = (sin 6^s -sin<7)/cos<7, где q = Q^A.

Найдем решение системы (19) в виде:

pQ = D^/ D^q , j = 0^2,                   (6)

где D^ - определитель системы; D^ - определитель, получаемый из D^ заменой элементов у-го столбца свободными членами системы.

Для решения задачи по определению КК акселерометров ИНС-В в качестве исходной информации используем известные векторные равенства, выражающие зависимости векторов ускорений точек Од, О_в твердого тела от ускорения точки Оу этого тела (в нашем случае - объекта):

W^A =^ + ехЛ^л+Пх(ох^),         (7)

W^B = ^ + exZ^b+Qx(qxZ^s),         (8)

где W — вектор ускорения точки Оу объекта; Q, е - векторы угловой скорости и углового ускорения объекта соответственно; L^A =O_YO_A, L^B =O_YO_B - радиус-векторы положения точек Од, О_в относительно ТОЧКИ Оу (рис. 1).

W^A = A^A + g;                         (9)

W^B=A^B+g,                     (10)

где, согласно допущению, g - вектор гравитационного ускорения любой точки объекта; А^а, А^в - векторы кажущихся ускорений точек Од, О_в объекта.

Обозначим символами WA, WB вектор W, входящий соответственно в первое и второе полученные равенства, фиксируя этими обозначениями факт «определения» этого вектора на основе информации соответственно с ИНС-А, ИНС-В. Критерием неидеальности является вектор kW = WB-WA.(11)

С учетом (9), (10) перепишем (7), (8):

ЙД = Лл+5-ДД-Пх(пхД?),(12)

^s=Hs+5-e^Zb-Qx(qxZ5).(13)

После записи векторных равенств (12), (13) в скалярной форме, получим (j= 1,2):

MV, = Y.H^A⁸-a_t-W^B = W^B-W^A, (14)

2=1

где

W.^L = lf(H^AE-H^An²)-I^AB(H^AQ² + H^ae), (15) L^a, L^b, g, - заданные величины, Я, e - вычисляемые величины на основе измерений угла Q^A =q датчиком угла ИНС-А путем дифференцирования по времени:

Я = 9;                                  (16)

е = £                                 (17)

На основе сравнения этих величин можно определить выражения для М.⁸ , после чего можно определить КК акселерометров ИНС-В.

Сигналы А^в акселерометров ИНС-В имеют погрешности М^в, что можно записать в виде:

А^в=а^в+М^в,                  (18)

где а^в — точные значения проекции вектора кажущегося ускорения точки О_в объекта в СК 2^s, входящие в выражения моделей (1), (2).

Тогда из (14) получим:

№» =

2=1

= а, -ЦН^^ва^в + АЖ, +^^£, z = 1, 2.    (19)

2=1

Уравнения (19) запишем в виде:

Н^\АВ + НАВ^ = Fx;

Н^М^ + Н^М₂ = F₂, где F, = Аб, cos q,.

Решив эту систему, найдем:

;mb=habfx-habf2, мв =h^f2-habfv где

Р,=а, + MV, + W⁸-(^H^ а^в + НД^ва₂), / = 1,2. (21)

Имеет место векторное равенство:

а⁸ =а^А -exL⁴⁸ -Qx^xL⁴⁸),        (22)

которое в скалярной форме есть: 2

a⁸ ^H^aj+W⁸, i = 1,2.         (23)

2=1

Таким образом, правые части уравнений (2) известны.

Найдем КК акселерометров ИНС-В, используя переобозначение:

Ы^М⁸, i = 1,2.                (24)

Используем уравнения (2), где величины АЛ, определены для трех разных моментов времени t_k, k = V3.

P^P^Pn^^

.Р^А*Р^Аа^в₂₊Р^Аа^в₂=^₂,           (25)

^о + ЛДв + ^з = Мз> * = 1- 2.

Найдем решение систем (25) в виде:

рА = d^ ]d^a , z = 1, 2, j = оД. (26) где D^a - определитель системы; D^A - определитель, получаемый из D^A заменой элементов у-го столбца свободными членами системы.

• 3.    К решению задачи разработки имитационной модели процедуры определения КК ИНС-В

Для решения задачи разработки ИМ определения КК необходимо задать:

Алгоритм функционирования имитационной модели процедуры калибровки...

• •    модели (имитаторы) измеренных величин: сигналов датчиков углов и сигналов акселерометров ИНС-А, ИНС-В;

• •    модели (имитаторы) определяемых КК площадки и акселерометров ИНС-В;

• •    критерии точности определения КК.

Модели сигналов датчика угла площадки и акселерометров ИНС-А зададим в виде:

Q^A = q = a? sin co/;                        (27)

a; = a_i2/² + a_n/ -g„ z = 1, 2.               (28)

Для задания сигналов датчика угла площадки и акселерометров ИНС-В необходимо вначале задать соответствующие модели погрешностей дрейфа площадки

Аб⁵ = Р^ + Р^ а^в + Р^ а^в,              (29)

где Р®, j = 0, 2 - модели (имитаторы) КК площадки ИНС-В, и акселерометров:

АД- ^ М= = Р^А + Р^Аа_х + Р^Аа₂, z = 1, 2, (30)

где Ру , / = 1, 2, у = 0, 2 - модели (имитаторы) КК акселерометров ИНС-В.

Модель погрешности для угла площадки ИНС-В имеет вид:

Ag5=Ag5(/0)+jAg5(/)^/,(31)

<0

а значит, модель сигнала датчика угла площадки ИНС-В:

QB=q^QB.(32)

Имея (30), можно определить модели сигналов акселерометров ИНС-В

Ав = aB+Mj, i = V2.(33)

В качестве критериев точности определения КК введем величины относительных погрешностей КК:

S? = |pf - pQ\/pf ,j = 6/2;(34)

Sy = |^ - Py \!p^, i = 1, 2, j = 5Д, (35) где в качестве эталонных значений выступают заданные модели (имитаторы) КК: Р~, Ру .

Введем величины вида: 1 2

1 2 2

^=тЕ2Х             (37)

° 1=1 у=0

представляющие собой средние арифметические величины относительных погрешностей всех КК площадки (5е) и относительных погрешностей всех КК акселерометров (5^) и принимаемые в качестве обобщенных критериев точности алгоритма функционирования имитационной модели (ИМ) процедуры калибровки.

• 4.    Решение задачи разработки алгоритма функционирования ИМ процедуры определения КК

Предполагаем, что:

• •    процедура калибровки ИНС-В начинается сразу после окончания процедуры выставки ИНС-В на основе информации с ИНС-А;

• •    в первую очередь осуществляется калибровка акселерометров ИНС-В, а затем - калибровка площадки ИНС-В;

• • калибровка акселерометров осуществляется за малое время. В этом случае можно допустить, что в течение всего интервала времени калибровки акселерометров ориентация площадки ИНС-В совпадает с ориентацией площадки ИНСА, а значит, в этом случае Ад = 0.

Определим значения исходных параметров.

Значения моделей КК площадки ИНС-В зададим такими, чтобы выполнялись условия:

l^+peg+^I^Ag,,(38)

где Ад, - заданная модельная величина дрейфа (ухода) площадки ИНС В. Из (38):

Рое=1/ЗАд„ (с4);

■^ = l/3-Ag./g, (с/м);(39)

pQ=\l3AQ,lg, (с/м).

Значения моделей КК акселерометров ИНС-В зададим из условий l^o+^g + T^AA,(40)

где ДА. - заданная модельная величина абсолютной погрешности измерения ускорения. Из (40)

7$ =1/3 АД, (м/с2);

• Р^ = 1/3-АД/g, (безразмерная);(41)

Р^ = 1/3 ■ АД /g, (безразмерная).

В качестве исходных параметров о проекциях вектора кажущегося ускорения целесообразно иметь средние значения соответствующих проекций на интервалах времени [0; /2], [0; /3], т.е. величины вида

4 = — J^ (t)dt, z = 1,2, к = 2,3.         (42)

^tk о

Подставив (28) в (42), получим:

^ =— [(ai2f2+ant-g,)dt,

*к 0

ИЛИ aik ~ ^Ьк ^l^^il^k ^V^^iAk ~ SAk) ’

ИЛИ

<4 = l/3a,₂/² +l/2a_n/_t -g„ i = 1,2, к = 2,3. (43)

Полагая к = 2, 3, запишем (43):

(1/3 /j) a,₂ + (1/2 /₂ ) a„ = <4 + g,;

1                                                  (44)

(1/3 /₃²) a,₂ + (1/2 /₃ ) а_л = 4 + g,.

Решая систему (44) относительно а/ь а(2, получаем а^.=^/^,(45)

где обозначено:

^оо ="" 1/6 (?з - ?2 ) ^з;(46)

D” ^Z2^ +g,)-l/2/3^ ^(47)

D=» =1/2/3(^ + g,)-l/2/2(^ + g,).(48)

Если ввести коэффициенты кратности g, то 4=^g, / = 1,2, ^ = 2,3.(49)

Задавая К^, вычисляем а^ по формулам (49), затем вычисляем D^, D^ по формулам (46)-(48) и находим коэффициенты а,у, необходимые для получения модели сигналов акселерометров ИНС-А.

Алгоритм функционирования ИМ процедуры определения КК представляет собой последовательность действий:

• 1.    Задать: g - модуль g (м/с²); Г_о = 0 - начальный момент времени (с); t_x, t₂, t₃ - первый, второй, третий моменты времени (с); Т - конечный момент времени; N_B , N_L- количество точек решения, вывода; а^е - амплитуда угловых колебаний (рад); со -частота угловых колебаний (с^-1); KS, KS, К₂₂, к^ (-); 1^, ^, iL 4 (м); Р^, (с"¹); Р?, Р^ (м/с); Р^А_й , Р₂1, (м/с²); Д4 , Р^А , Р^ , /% Н-

• 2.    Д/ = (Г-/_О)/А_В; 4 по (49); D^, D^ DS по (46)-(48); а_у по (45); L^AB=L^B-L^A, / = 1, 2; t = t₀.

• 3.    AQ^B =0, Ag = 0.

• 4.    t_p = t + Дt, t_pp = t + 2M

• 5.    9=a^sinco/, q_p =a-sino)Z_/,, q_pp=a~ s\ntot_pp no (27); a, no (28).

• 6.    ^^p-q^At; £ = ^_Pp-2q_P+qV^^t)² (численное дифференцирование (ЧД)), H^A_X = cosq, Н^А₂ = -sin q, H_2X = sin q,      H^A₂₂ = cos q,

• 7.    H^B = ^ H^H^A , i, j = 1, 2; W® no (15). m=l

• 8.    a® no (23).

• 9.    A^⁵, A4, no (29), (30).

• 10.    AQ^B =^^в+Дб^ВМ (ЧД).

• 11.    Q^B =q + kQ^B; Л® =а^в +M,, z = l, 2 no (32), (33).

• 12.    Ag = (sin Q^B - sin ^)/cos q;   W,^A , W^B ,

• 13.    ^W_l=W^в-W_l^A, / = 1,2; F, no (21).

• 14.    A^ no (20).

• 15.    t = / + А/, t_p = Z + AZ , t_pp = 1тШ

• 16.    <7 = a^sinco/, q„ =a^esinoy_n, o„=a^esin(nZ_m no (27).

• 17-    Q = p-q)/^; E = (q_pp-2q_p+q^(&tf; H_xx = cos q, H^A₂=-sm.q, H_2X=smq, H₂₂=cosq; ^^^s=cos(A0, H^ = -sin(A0, H₂^=sin(Ag), H^ =cos(A0.

• 18.    H^B = ^H^H^A, i,j = l,2; W^, a, no m=l

• 19.    a^B no (23).

• 20.    A^⁵ no (29).

• 21.    A0^S =Ag^S+Ag⁵A/ non. 10.

• 22.    Q^B =q + ^Q^B non. 11.

• 23.    AQ_p =(sinQ^B -smq)/cosq.

• 24.    дё = (дд_р-дд)/м (чд).

• 25.    Если (/>/,-0,5A/) и (/ x +0,5А/), то Ай =Аё; ДА1 =М; 4 =а^В, / = 1, 2.

• 26.    Если (/>/₂-0,5А/) и (/ 2 +0,5А/), то Д0 =АЙ; М,₂ =М_Х; а^в=а^в, i = l, 2.

• 27.    Если (/>/₃-0,5А/) и (t3 +0,5А/), то дёз =Аё; Мз =М; ^з =«Л 1 = 1, 2.

• 28.    t = t + M.

• 29.    Если t < Т, то п. 4.

• 30.    pQ, Р^ по (6), (26).

• 31.    Sf, S^ по (34), (35).

• 32.    S^Q, S^A по (36), (37).

• 33.    Вывести: pQ, S^, S^Q, P^, S^, S^A.

• 34.    Закончить.

H® = cos(A0, H^ = -sin(A0, H^ = sin(A0, H^AB =cos(A0.

A^, no (14).

(15), (28).

Заключение

На основе этого алгоритма разработана программа, реализующая имитационную модель процедуры определения КК для трехосной стабилизированной платформы (ТСП) и трех акселерометров ИНС-В (рис. 2), на вход которой подается информация о номерах акселерометров (z), а значит, и об ориентации оси площадки, о проекциях вектора гравитационного ускорения (G/) и проекциях радиус-векторов начал связанных с ИНС-А, ИНС-В систем координат (Д), моделях сигналов датчиков углов

Алгоритм функционирования имитационной модели процедуры калибровки...

ИНС-А, ИНС-В (q_b Q) и моделях сигналов акселерометров ИНС-А, ИНС-В (а„ А), а выход которой -величины КК платформы и акселерометров (рис. 3).

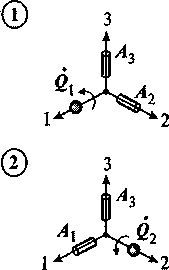
Аё^+^2+^3;

• - АЛ₂ = Тэд ⁺ ^22^а2 ⁺ р23^а3’ АА₃ = Р30 +^32^2 + Р₃₃а₃.

^Ог ⁼ ^20 ⁺ ^^а1⁺ ^^а3’

• • АЛ, = /jo + 7ц а₃ + 71з ^аз >

А^з = Р₃₀ + Р31 ^1 + Тзз а₃.

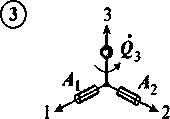
'^Р^Р^М-Р^, " ^А ⁼ ^10 ⁺ ^ ^а1 ⁺ ^12 ^а2 ’

А^2 = ^20 + ^21<21 + -^22а2-

Рис. 2. Варианты установки датчиков и математические описания для подсистем 1, 2 и 3