Алгоритм и информационные технологии построения оптимальной ассортиментной политики предприятия

ВЕСТНИК 2015

В условиях финансового кризиса, дороговизны заемных ресурсов, риска оказаться в кредитной ловушке с перспективой потери бизнеса для коммерческого предприятия особенно актуальным становится поиск альтернативных источников финансирования.

При определенных условиях предприятие может изыскать дополнительные необходимые финансовые ресурсы за счет собственных средств.

Варианты выбора очередности финансирования проекта

Проанализируем возможные варианты выбора проектов. Ограниченность средств предполагает приоритеты в финансировании и ранжирование проектов по определенному критерию, в данном случае - по эффективности проекта. Существует немало известных способов опреде- ления эффективности и выбора проектов из ряда предлагаемых на основе критериев внутренней доходности (IRR) и других показателей.

Предлагается рассмотреть метод выбора очередности финансирования на основе маржинальной рентабельности.

Пусть имеется n проектов [3]. Возможное число размещений из n проектов по n определяется перестановкой из n элементов и рассчитывается по формуле A n = n !. Предположим, число проектов равно пяти, тогда количество перестановок (число) будет равно 5! = 120. Ста двадцатью различными способами (по очередности финансирования) можно расставить пять проектов.

Рассмотрим графики очередности финансирования проектов (рис. 1). При принятом критерии (в нашем случае эффективность) на графике найдется один лучший вариант (1), один - худший (2) (проектов с равной, максимальной или минимальной эффективностью может быть несколько, но это не меняет сути). Остальные 118 вариантов будут располагаться между ними (3).

Самым худшим выбором является выбор, обратный лучшему, то есть соответствующий критерию наименьшей эффективности. При этом проекты ранжируются по возрастанию маржинальной рентабельности. Последние и первые проекты меняются местами.

Чтобы представить всю серьезность рассматриваемой задачи, скажем, что уже для 10 проектов теоретически существует 3 628 800 различных вариантов выбора. Один (или несколько) лучше остальных, с точки зрения максимальной финансовой отдачи.

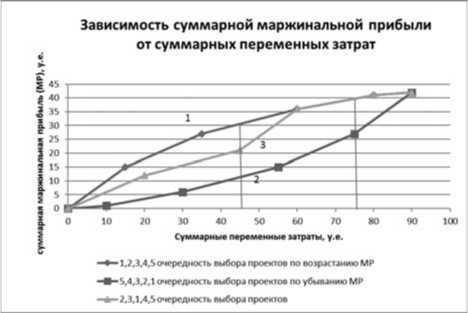
Рис. 1. Зависимость маржинальной прибыли от суммарных переменных затрат по проектам

Маржинальная рентабельность портфеля в целом или средняя маржинальная рентабельность по портфелю есть отношение суммарной маржинальной прибыли к суммарным затратам. Очевидно, в портфеле есть проекты с большей и меньшей маржинальной рентабельностью, чем средняя. При возникновении ограничений на финансы возникает необходимость приостановки финансирования портфеля проектов на недостающую сумму. Нужен простой, надежный механизм гарантирующий сохранение финансирования наиболее выгодным проектам (с точки зрения максимальной финансовой отдачи).

Маржинальная рентабельность есть отношение маржинальной прибыли к переменным затратам. Геометрически – это тангенс угла наклона отрезка, характеризующего данный проект к горизонтальной оси. Принцип убывания маржинальной рентабельности означает, что тангенс угла наклона каждого последующего отрезка меньше предыдущего. Соответственно, получается ограниченная сверху выпуклая вверх параметрическая кривая. То есть, площадь под этой кривой является максимально возможной из всех возможных вариантов их расположения. На рис. 1 – это кривая 1.

В общем виде оптимальная кривая носит степенной характер. Показатель степени положительный и меньше единицы:

y = x p , 0 <  p <  1 ,              (1)

n где p = —, n и m - натуральные числа, n < m.

m

Функция монотонно возрастает, не имеет экстремумов, выпукла вверх.

Функция, позволяющая находить выигрыш между оптимальным и средним способами реализации проектов находится по следующей формуле:

y = Ax^p - Bx ,               (2)

где A и B – масштабные множители.

y = Bx                (3)

прямая среднего распределения проектов.

Дифференцирование уравнений (2) и (3) и их последующее решение дает возможность определить максимальную разницу в результате.

Максимум достигается при x=m

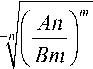
nm

, I An im-n      । An im-n y = AI       I - BI       I

I Bm )       \ Bm )

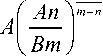
B ( An i

¹ ;i I

A V Bm )

Пример практических расчетов по разности выигрыша между наилучшим и средним вариантами выбора проектов приведён на рис. 4.

Производная уравнения (2) отрицательна, кривая выпукла вверх.         ₁

Для случая n = 1, m = 2, p =— выигрыш между оптимальной и средней кривыми будет иметь следующий вид:

y = A4x - Bx ,             (6)

где A и B – масштабные множители.

На рис. 2 это область между кривой и прямой линиями.

ВЕСТНИК 2015

Зависимость маржинальной прибыли от суммарных переменных затрат

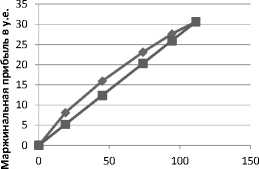
Зависимость сумм. МП от сумм. ПЗ зависимость сумм. МП по итоговой МР от сумм. ПЗ

Суммарные переменные затраты в у.е.

Рис. 2. Зависимость максимальной и средней маржинальной прибыли от суммарных переменных затрат

Максимум достигается при

A2

x=      , y=

4B2

Для полноты рассмотрим еще один случай, а именно: разницу между наилучшим и наихудшим распределением проектов (кривые 1 и 2 на рис. 1).

В общем виде функция кривой 2 носит степенной характер, степень больше единицы (функция кривой 2 является обратной к функции кривой 1). Функция кривой 2 имеет следующий вид:

m y = Bxⁿ .

Тогда функция разности между прямой и обратной функциями будет иметь вид:

nm y = Ax^m - Bxⁿ .

Дифференцирование уравнений (8) и (9) дает возможность определить координаты точки мак- симума:

y = A

' An 2_ I Bm m

mn

2 2 An ² m - n

Bm ²

ВЕСТНИК 2015

I m - n )

B ^ An ²^ ^{m 2 n 1}

A ( Bm ² J

Результаты практических расчетов по фактическим опытным данным по разности выигрыша между наилучшим и средним и наилучшим и наихудшим вариантами выбора очередности финансирования проектов приведены на рис. 3 и 4, соответственно.

Производная уравнения (9) отрицательна, кривая выпукла вверх.

Алгоритм выбора выгодного ассортимента

Шаг 0. (Подготовительный). Составляется таблица, куда заносятся результаты всех последующих шагов.

Пример построения таблицы – по алгоритму (см. табл. 1). В таблицу уже внесены данные пяти проектов.

Шаг 1. Формируется перечень бизнес-проек-тов. Графа 1.

Шаг 2. Для каждого бизнес-проекта рассчитывается ожидаемая выручка в течение заранее заданного срока. Графа 2.

Шаг 3. Определяется процент маржинальной прибыли в выручке. Графа 3.

Шаг 4. Рассчитывается величина маржинальной прибыли для каждого бизнес-проекта (результат шага 2 умножается на результат шага 3). Графа 4.

Шаг 5. Для каждого бизнес-проекта рассчитываются переменные затраты (результат шага 2 – соответствующий результат шага 4). Графа 5.

Шаг 6. Рассчитывается маржинальная рентабельность для каждого бизнес-проекта (результат шага 4 делится на соответствующий результат шага 5). Графа 6.

Шаг 7. Ранжируются бизнес-проекты по данным шага 6. Графа 7.

Шаг 8. Расставляются в таблице бизнес-проекты согласно данным о ранжировании (графа 7) в порядке возрастания номеров.

Шаг 9. (Оптимальное распределение). Рассчитываются суммарные значения маржинальной прибыли (данные графы 4 после ранжирования выписываются для бизнес-проектов накопительным итогом). Графа 8.

Шаг 10. Рассчитываются суммарные значения переменных затрат (данные шага 5 выписываются для бизнес-проектов накопительным итогом). Графа 9.

Шаг 11. Рассчитывается средняя по всем проектам маржинальная рентабельность (данные графы 8 делятся на соответствующие данные графы 9). Графа 10.

Значение средней по всем финансируемым проектам маржинальной рентабельности есть последнее значение в графе 10.

Шаг 12. Значение средней по всем финансируемым проектам маржинальной рентабельности (последнее значение в графе 10) заносится во вспомогательную графу 11. Графа 11.

Шаг 13. (Неоптимальное распределение). Рассчитывается маржинальная прибыль для всего портфеля по средней маржинальной рентабельности (значение средней маржинальной рентабельности из графы 11 умножается на значения переменных затрат нарастающим итогом из графы 9, данные шага 10). Графа 12.

Шаг 14. Находится выигрыш маржинальной прибыли в зависимости от выбранной стратегии. Например, между лучшим и средним распределением проектов (рис. 3) при наличии дефицита финансирования. Из данных шага 9 (графа 8) вычитаются соответствующие значения данных шага 13 (графа 12). Расчеты выигрыша между лучшей и худшей стратегиями, между средней и худшей стратегиями показаны на рис. 4 и 5, соответственно.

Шаг 15. В графу 14 вносятся данные маркетологов о приросте выручки по рассматриваемым проектам. Графа 14.

Шаг 16. Строится параметрическая зависимость между изменением маржинальной рентабельности от проекта (данные графы 5 после

Таблица 1

Таблица для расчета выгодного ассортимента

В Й Р О Рч К	cd ^ К о m	к S	CD о ^н S ^ Н m К а S	86 СП к	о хо О Рн ^ in ^		3 g 8 и s ^ н £ § У 5 8 & И К S	3 g 8 и И у 9 ^ 2 У н 8 св & И го К	g о S HS 2 * cd /—^ Н <^ cd ооу Рч^ cd К ^ S	Р-Г О t< PQ g К	2 ^? cd ^ g^ о ^ ® о Ч t^ н >^ ^ S . К   О CD    ^ О К S	И 2 Э К И 8 см 2 и и 3 « | s s у Э з g В и Я у & а о g я ^^2 m ю	S н >^ о 2 Рч СО ^ Я О Рч К
Проект 1	27	30	8	19	43	1	8	19	43	27	5	3	40
Проект 2	34	23	8	26	30	2	16	45	35	27	12	4	35
Проект 3	36	20	7	29	25	3	23	74	31	27	20	3	40
Проект 4	25	18	5	21	22	4	28	94	29	27	26	2	50
Проект 5	20	15	3	17	18	5	31	111	27	27	31	0	15

Проект – мероприятия по выпуску конкретного ассортимента продукции;

У.е. – условные денежные единицы;

МП – маржинальная прибыль;

ПЗ – переменные затраты;

МР – маржинальная рентабельность

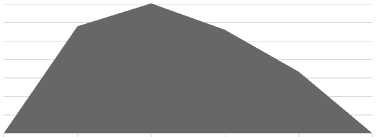
Выигрыш лучшей стратегии по сравнению со средней

a

3,5

2,5

1,5

0,5

Затраты, тыс. у.е.

Рис. 3. Выигрыш лучшей ассортиментной стратегии по сравнению со средней

Выигрыш средней стратегии по сравнению с худшей

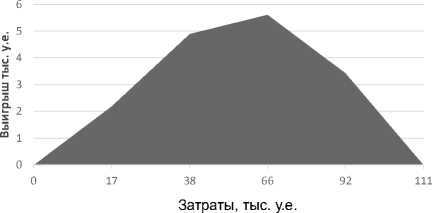
Рис 5. Выигрыш средней ассортиментной стратегии по сравнению с худшей

ВЕСТНИК 2015

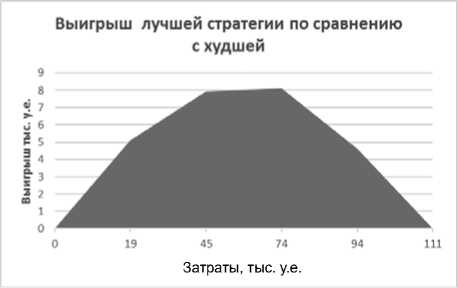
Рис. 4. Выигрыш лучшей ассортиментной стратегии по сравнению с худшей

ранжирования). По левой (основной) вертикальной оси откладываются проценты, по основной горизонтальной оси откладываются наименования проектов после ранжирования. По второй (вспомогательной, правой) вертикальной оси откладываются данные соответствующих значений маржинальной прибыли, выручки и планируемой выручки по данным маркетологов (данные из соответствующих граф 2, 4, 14), рис. 6.

Как видно из табл. 1 и рис. 6, самыми выгодными проектами с точки зрения максимальной выручки являются 3 и 2. С точки зрения максимальной выручки (прогнозируемой) на будущий

Зависимость между МР, МП, выручкой

Проекты

МП

выручка        выручка, прогноз        МР

Рис. 6. Параметрическая зависимость между изменением маржинальной рентабельности от проекта

ВЕСТНИК 2015

период лучшим является проект 4. С точки зрения максимальной маржинальной рентабельности (отдача по маржинальной прибыли на единицу вложения переменных затрат) лучшим является проект 1.

Предложенный алгоритм позволяет увеличить финансовые результаты без привлечения внешних заимствований. Для этого руководителю необходимо перебросить финасовые и материальные ресурсы с проектов 3, 4 и 5 в проекты 1 и 2 – до уровня достижения пределов продаж. Если после такого перераспределения средства еще останутся, то их следует вложить в следующий по маржинальной рентабельности проект. И так далее, пока не будут вложены все ресурсы.

Когда нет ограничений на затраты, результат финансирования одинаков по всем 120-ти вариантам выбора очередности запуска пяти проектов в производство.

Разница возникает при наличии дефицита финансирования. Если в наличии не 90 тыс. условных единиц, а 75 (дефицит бюджета 16,7%), то выбор проектов по способам 1 и 3 дают 40 тыс. у.е. маржинальной прибыли, а способ 2 – только 27 тыс. у.е., т.е. на 33,5% меньше (рис. 1).

Если дефицит составляет 50%, то способ 1 дает маржинальную прибыль 30 тыс. у.е., способ 3 – 20 тыс. у.е., а способ 2 – 12 тыс. у.е. Раз- ница составляет 33% и 60%, соответственно (рис. 1).

Рентабельность и прибыль проекта зависят от способа разнесения постоянных затрат по всем проектам (например, пропорционально объему продаж или фонду заработной платы). Постоянные затраты меняются слабо от изменений объемов выпуска, поэтому сокращение по одному проекту приводит к росту затрат по другим проектам. В способе разнесения постоянных затрат заложена скрытая опасность, по формальным признакам в аутсайдерах может оказаться эффективный проект. При дефиците финансирования он будет закрыт [4]. Предложенный метод позволяет при наличии дефицита финансирования избежать закрытия проекта с большей маржинальной рентабельностью.