Алгоритм и практическое применение метода Хука-Дживса

Метод Хука-Дживса работает путем итеративного создания набора направлений поиска. Созданные направления поиска должны быть такими, чтобы они полностью охватывали пространство поиска. Другими словами, они должны быть такими, чтобы, начиная с любой точки пространства поиска, можно было достичь любой другой точки пространства, двигаясь только по этим направлениям. В N-мерной задаче для этого требуется по меньшей мере N линейно независимых направлений поиска. Например, в функции с двумя переменными для выполнения поиска требуется по крайней мере два направления из любой одной точки в любую другую точку. Среди множества возможных комбинаций из N направлений поиска некоторые комбинации могут привести к месту назначения быстрее (с меньшим количеством итераций), а некоторые могут потребовать большего количества итераций.

В методе Хука-Дживса комбинация исследующего поиска и поиска по образцу выполняется итеративно. Исследующий поиск выполняется вблизи текущей точки систематически, чтобы найти наилучшую точку вокруг текущей точки. После этого две такие точки используются для поиска по образцу.

Опишем исследующий поиск. Предположим, что текущее решение (базовая точка) обозначается через х _с. Установим i = 1 и х = х с

Шаг 1. Вычисляем f = f ( x ), f + = f ( x _i + Δ i ) и f – = f ( x _i – Δ i ).

Шаг 2. Найдем f _min = min( f , f +, f –). Значение соответствует f _min.

Шаг 3. i = N ? Если нет, устанавливаем i = i + 1 и переходим к шагу 1;

В противном случае x является результатом и переходим к шагу 4.

Шаг 4. Если x = x _c, то поиск завершился успешно; в противном случае - нет.

В исследующем поиске текущая точка движется в положительном и отрицательном направлениях по очереди, и запоминается наилучшая точка. Текущая точка изменяется на наилучшую точку в конце каждого шага. Если точка, найденная в конце всех шагов, отличается от исходной точки, исследующий поиск считается успешным; в противном случае исследующий поиск является неудачным. В любом случае, лучшая точка считается результатом исследующего поиска.

Рассмотрим поиск по образцу. Новая точка определяется путем перехода от текущей наилучшей точки вдоль направления, соединяющего предыдущую наилучшую точку x _c и текущую базовую точку x ( k ) следующим образом:

xp ( k + 1) = x ( k ) + ( x ( k ) - x ( k -1))

Метод Хука-Дживса включает в себя итеративное применение исследующего поиска в местоположении текущей

точки и последующий переход с использованием поиска по образцу. Если поиск по образцу не приводит к перемещению решения в лучшую область, поиск по образцу не принимается и область исследующего поиска уменьшается.

Алгоритм работает следующим образом:

Шаг 1. Выберем начальную точку x ( 0 ), переменные инкременты Δ i ( i = 1,2,…, N ), коэффициент уменьшения шага α >1 и параметр завершения ∈ . Установим k = 0.

Шаг 2. Выполним исследующий поиск с x ( k ) в качестве базовой точки. Скажем, что x — это результат исследующего поиска. Если исследующий поиск прошел успешно, установим z ( k + 1) = x и переходим к шагу 4; В противном случае перейдем к шагу 3.

Шаг 3. |Δ| <  ∈ ? Если да, алгоритм завершается; В противном случае установим A = A/α для i – 1,2,…, N и переходим к шагу 2.

Шаг 4. Установим k = k + 1 и выполним поиск по образцу:

xp ( k + 1) = x ( k ) + x ( k ) – x ( k + 1).

Шаг 5. Выполним еще один исследующий поиск, используя x _p в качестве базовой точки. Пусть результатом будет x ( k + 1).

Шаг 6. f ( x ( k + 1) <  f ( x ( k ))? Если да, перейдем к шагу 4. В противном случае перейдем к шагу 3.

Стратегия поиска достаточно проста. Алгоритм требует меньшего объема памяти для переменных; на любой итерации необходимо сохранять только две точки (x(k) и x(k+1)). Численные расчеты, связанные с этим процессом, также просты. Но, поскольку поиск в значительной степени зависит от перемещений по координатным направлениям (xi, x – z и т.д.) во время исследующего поиска, алгоритм может преждевременно прийти к непра- вильному решению, особенно в случае функций с сильно нелинейной зависимостью между переменными. Алгоритм также может оказаться в цикле исследующего поиска, либо между шагами 5 и 6, либо между шагами 2 и 3.

Другой особенностью этого алгоритма является то, что он завершается только поиском в окрестности сходящейся точки. Это требует большого количества вычислений функций для сходимости к решению с разумной степенью точности. Сходимость к оптимальной точке зависит от параметра a. Рекомендуемое значение a = 2.

Проверим работу реализации алгоритма Хука-Дживса, написанную на языке программирования C++, на данных функциях: Розенброка, Химмельблау, Матьяса, Бута и МакКормика.

Функция Розенброка – невыпуклая функция, заданная формулой:

f ( x , y ) = (1 – x )² + 100( y – x ²)²

Она имеет глобальный минимум в точке ( x , y ) = (1,1), где f ( x , y ) = 0

На рисунке 1 представлен график данной функции.

Сравним результат, полученный при выполнении алгоритма Хука-Дживса, с известным глобальным минимумом.

При начальных значениях точек 5 и -5 и при шаге 0,4, мы получим результат x ₁ = 1, x ₂ = 2 с минимум в точке 0 за 31 поиск по образцу.

Функция Химмельблау – мультимодальная функция двух переменных, заданная формулой f (x, y) = (x2 + y – 11)2 + (x + y2 – 7)2

Она имеет локальный максимум с координатами x ≈ -0,270845, y ≈ -0,923039 и значением f ( x , y ) ≈ 181,617 и четыре равнозначных локальных минимума:

f (3,2) = 0,

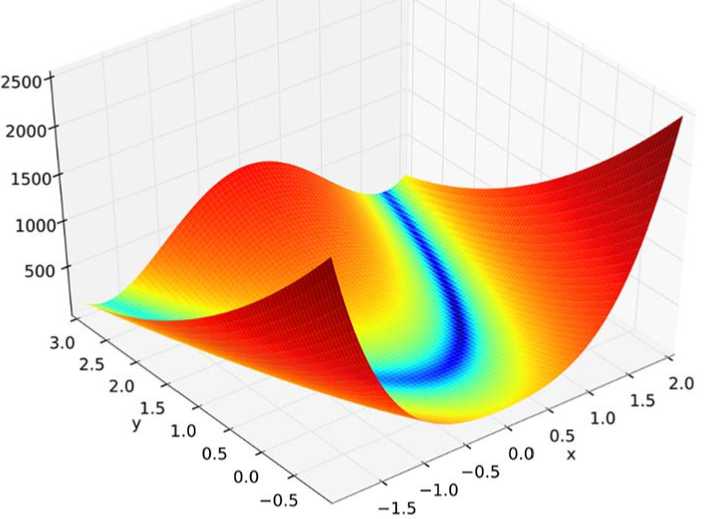
Рисунок 1. График функции Розенберга для двух переменных

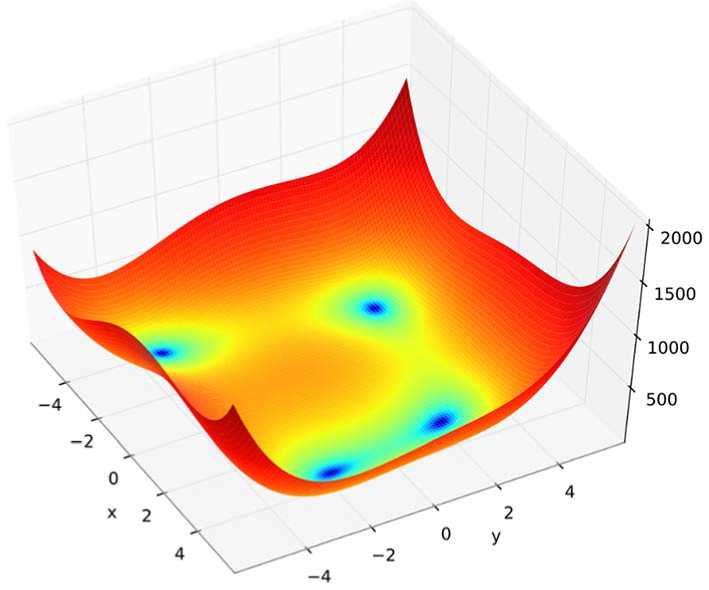
Рисунок 2. График функции Химмельблау для двух переменных

f (-2,805118; 3,131312) = 0, f (-3,779310; -3,283186) = 0, f (3,584428; -1,848126) = 0.

На рисунке 2 представлен график данной функции.

Сравним результат, полученный при выполнении алгоритма Хука-Дживса, с известным глобальным минимумом.

При начальных значениях точек 5 и 5 и шаге 1, мы получим результат x1 = 3, x2 = 2 с минимум в точке 0 за 2 поиска по образцу. При начальных значениях точек -5 и -5 и длиной шага 0,2, мы получим результат x1 = -3.77932, x2 = -3.28318 с минимум в точке 0 за 17 поисков по образцу. При начальных значениях точек -2 и 3 и длиной шага 0,1, мы получим результат x1 = -2.80511, x2 = 3.13131 с минимум в точке 0 за 12 поисков по образцу. При начальных значениях точек 3 и -1 и длиной шага 0,1, мы получим результат x1 = 3.58443, x2 = -1.84813 с минимум в точке 0 за 16 поисков по образцу.

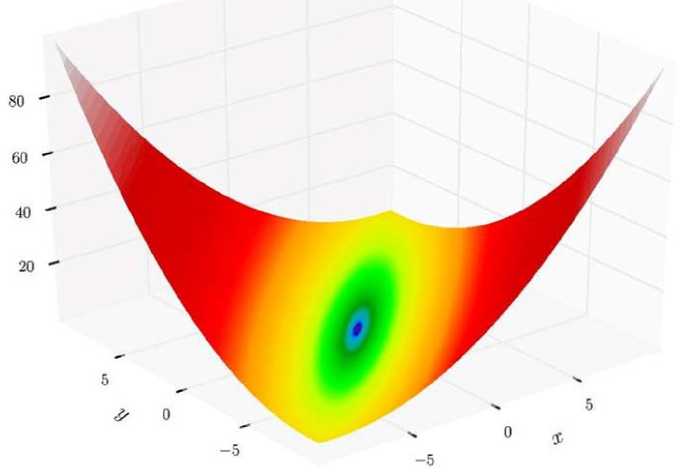
Рисунок 3. График функции Матьяса

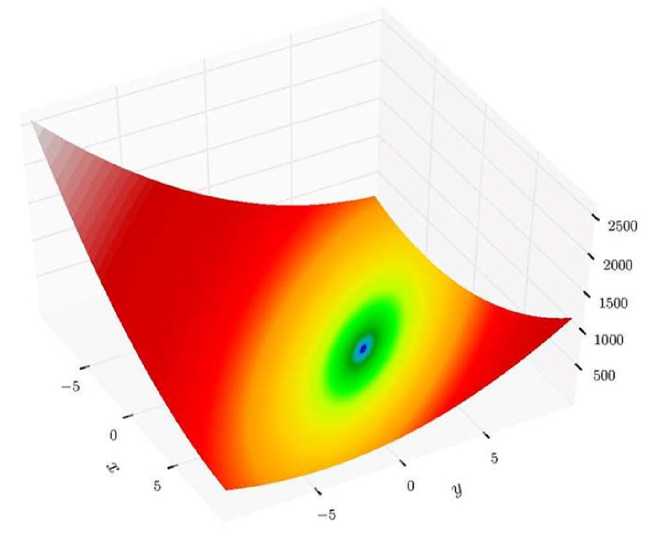
Рисунок 4. График функции Бута

Функция Матьяса задана формулой f (x, y) = 0.26 (x2 + y2) – 0.48xy

Она имеет локальный минимум в точке f (0,0) = 0.

На рисунке 3 представлен график данной функции.

Сравним результат, полученный при выполнении алгоритма Хука-Дживса, с известным глобальным минимумом.

При начальных значениях точек 0 и 4 и длиной шага 0.5, мы получим результат x ₁ = 0, x ₂ = 4 с минимум в точке 0 за 2 поиска по образцу.

Функция Бута задана формулой:

f ( x , y ) = ( x + 2 y – 7)² + (2 x + y – 5)²

Она имеет локальный минимум в точке f (1,3) = 0.

На рисунке 4 представлен график самой функции.

Рисунок 5. График функции МакКормика

Сравним результат, полученный при выполнении алгоритма Хука-Дживса, с известным глобальным минимумом.

При начальных значениях точек 5 и -10 и длиной шага 5, мы получим результат x ₁ = 0, x ₂ = 0 с минимум в точке 0 за 2 поиска по образцу.

Функция МакКормика задана формулой f (x,y) = sin(x + y) + (x – y)2 – 1.5*x + 2.5*y + 1

Она имеет локальный минимум в точке f (-0.54719, -1.54719) = -1.9133.

На рисунке 5 представлен график данной функции.

Сравним результат, полученный при выполнении алгоритма Хука-Дживса, с известным глобальным минимумом.

При начальных значениях точек 0 и -2 и длиной шага 1, мы получим результат x ₁ = -0.5472, x ₂ = -1.5472 с минимумом в точке -1.91322 за 12 поисков по образцу.

Анализ результатов говорит о хорошей сходимости метода Хука-Дживса.