Алгоритм идентификации параметров динамической системы второго порядка с малыми возмущениями по экспериментальным данным

Рассмотрим линейную систему обыкновенных дифференциальных уравнений c малыми возмущениями вида

[ lu = ^{9 1 X 1} + ⁹2^X2 + ^ 1 X 1

= ⁹3^X1 + ⁹4^X2 + ^£2^X2

где X f E R, i = 1,2 - зависимые переменные, t 6 [0, b] - независимая переменная, b > 0,

9k E R, к = 1,..., 4 - неизвестные параметры, ej (j = 1,2) - достаточно малые вещественные параметры.

Обозначим через X j (t, 9) - j-компоненту решения системы (1), j = 1,2, зависящую от векторного параметра в = column^, 9 2 ,9 3 ,9 4 ).

Пусть при некоторых фиксированных значениях в_к , к = 1, .,4 , решение системы (1)

удовлетворяет задаче Коши с начальными условиями:

x(1) = х1(0), х(1) = х2(0).(2)

Пусть так же по переменной х с шагом i = ^ на равномерной сетке ti = 0,.,ti+i = ti+i,.,tN = Ь,(3)

для экспериментальных данных справедливы соотношения

X(t) = x(f) + e(t), i = 1,...,N,(4)

где х(} = column(x(\x(f'),  х® = column^x® ^W)  х^1 = Xj(ti, в) - значение компоненты решения системы (1) в точке tf при фиксированном значении векторного параметра в, e(i = column(eii,. ,eiN) - вектор, элементы которого являются случайными величинами, имеющими стандартное нормальное распределение, то есть eij Е N(0,1), i = 1,N, j = 1,2.

Ставится задача идентификации параметров системы вида (1), заключающаяся в нахождении таких оценок в_к параметров в_к , к = 1, .,4, при которых решение задачи (1) приближается экспериментальными данными {x⁽ⁱ⁾, i = 1,N} в смысле метода наименьших квадратов [1].

Заменим уравнение (1) симметричной разностной схемой [2] на сетке (3)

у (i + i)_r(i) ХX

т у (i+i')

х2

т

= 2 ^(fi,i ⁺ f i+i,i ),

1(f.^f.

= 2 \fl2 + fl+1,2), i = 1,N -1, где fi,i = fi(x(l'), в) = eiX(i) + в2х21) + eiX^, fi,2 = f2(x(l\в') = взХ^ + в^ + е2х21\

Вводя обозначения [3]

z = column(x ^(N\ в ), x^(N) = column(x ⁽¹ \ ..,х ^(А/) ),

Z = column(x ^(N\ o₄ ), x ^(N) = column(x ⁽¹'⁾ , .„,X^(N)), o₄ - нулевой вектор размерности 4, получим

x(N) = Hiz, x(N) = HiZ, где

H1 — [I2N : 02Nx4],   ^2 = ^^1^1, здесь I2N - единичная (2N x 2М)-матрица, 02Nx4 - нулевая (2N x 4)-матрица.

Тогда, согласно [3-5], задача идентификации параметров может быть сформулирована как задача минимизации квадратичного функционала с ограничениями в виде нелинейных алгебраических уравнений

{ min m(z), m(z) — | (H₂z, z) — (H₂z, z)

T(z) — h                .                       ⁽⁶⁾

g(z) — о

Здесь введены следующие обозначения: T — [T 1 T₂, . ,T_N,T_e] - (2 x (2N + 4)) -матрица, T^, i — 2,N - нулевые (2x2) - матрицы, Tq - (2x4) - матрица;

g(z) — column^^,...,g N (z~) ), g i (z) — column(gn(z),g i2 (z)), i — 1,N, gM — gu(x^w,9) =

= (1+^1 + £1)) X? +102*2l) — (1 — I (^1 + £1)) x(l+1) + 102X(l+1),    (7)

g^z) — g i2 (x^w,e) =

= | в₃х1^П + (1+1(0 4 + 1 2 )) X® +1 _{в з Х}а⁺' > — (1—1( _в 4 ₊ £ 2 ) X™.    ⁽⁸⁾

Заметим, что разностная схема (5) с учетом обозначений (7)-(8) может быть записана в виде

g(z) — 0.

Для решения задачи (6) воспользуемся алгоритмом [3], основанным на аппроксимации исходной задачи последовательностью квадратичных задач минимизации с линейными ограничениями. На каждом шаге разреженная система линейных алгебраических уравнений большой размерности решалась с использованием метода сопряженных градиентов [4].

Вычисления проводились на трех наборах экспериментальных данных X^(l), i — 1,N, отличающихся от приближенных решений с начальными данными х 1 (0) — 1, x₂(0) — 1 системы (1) на случайные величины £ ij EN(0,1) (j — 1,2), имеющие стандартное нормальное распределение. Каждое приближенное решение системы (1) получено при фиксированном наборе параметров 0 ^ , к — 1, .,4, соответствующих трем типам особой точки системы (1): седло, узел, центр. Точность вычислений 8 полагалась равной 0.001.

В результате вычислений для трех различных наборов экспериментальных данных получены оценки 0 _к для параметров 0 ^ , к = 1, ...,4, а также компоненты x₁(t,0), x₂(t,0) приближенных решений системы (1) .

Приведем графики компонент x₁(t,f0), x₂(t, 0) приближенных решений системы (1) и соответствующие им экспериментальные данные.

Случай 1. Нулевое положение равновесия системы (1) – седло.

Получены следующие оценки параметров 0 1 , 0 2 ,0 3 ,0 4 :

0 1 = 2.02298, 0₂ = 0.0001, 0 3 = 0.00 0 02, 0₄ = -2.90 0 02..

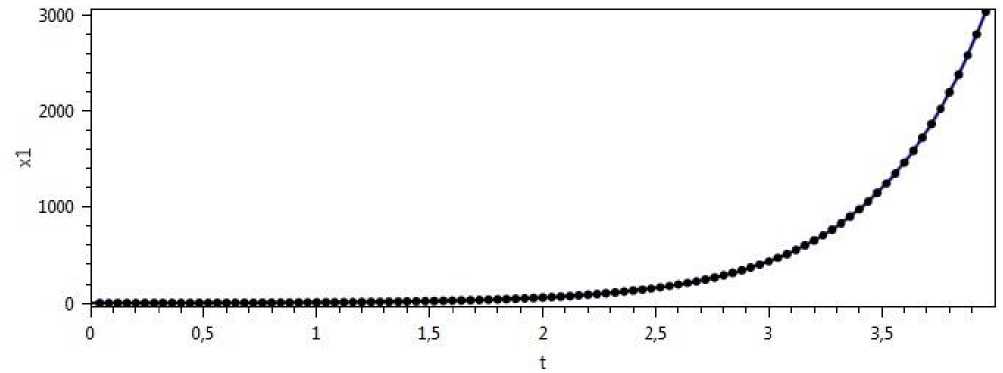
Рис. 1. Экспериментальные данные и график компоненты x 1 (t, 0) приближенного решения системы (1).

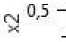
0 -

О              0,5              1              1,5              2              2,5              3              3,5

t

Рис. 2. Экспериментальные данные и график компоненты x2(t, 0) приближенного решения системы (1).

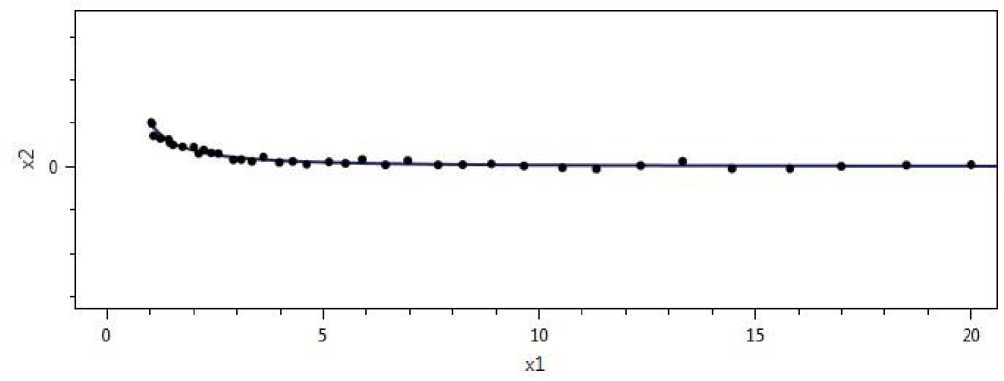
Рис. 3. Экспериментальные данные и приближение фазовой траектории системы (1)

с начальными данными х 1 (0) = 1, % 2 (0) = 1.

Случай 2. Нулевое положение равновесия системы (1) – узел.

Получены следующие оценки параметров 3 1 ,3 2 ,6 3 ,6 4 :

0! = -3.14132, 32 = 0.01895, З3 = 1.03559, 04 = 0.02129.

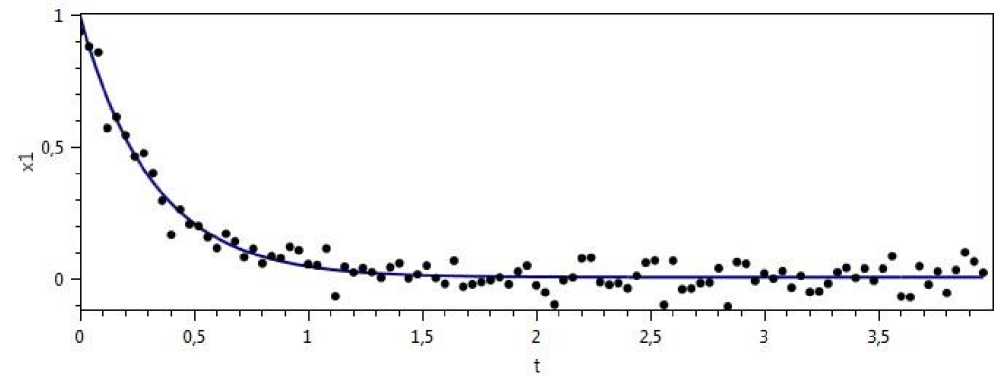
Рис. 4. Экспериментальные данные и график компоненты ^(t, 0) приближенного решения системы (1).

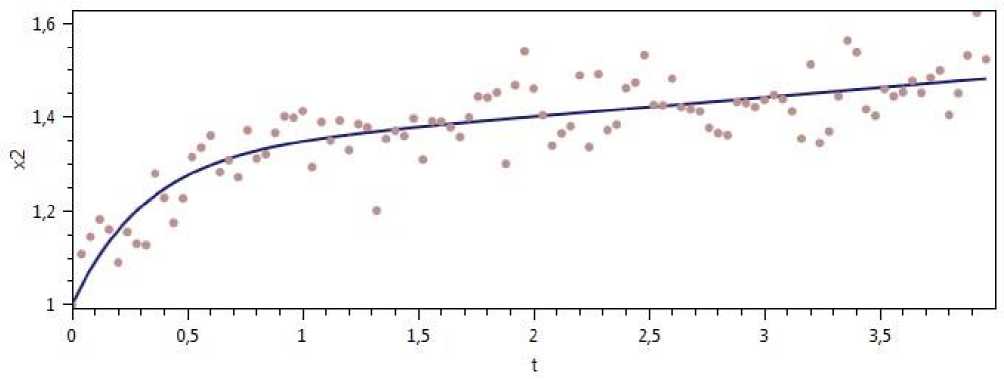
Рис. 5. Экспериментальные данные и график компоненты % 2 (t, 0) приближенного решения системы (1).

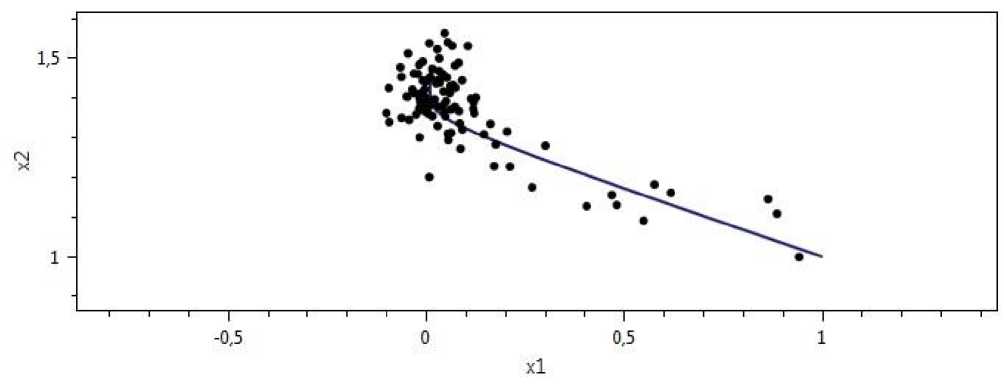
Рис. 6. Экспериментальные данные и приближение фазовой траектория системы (1) с начальными данными % 1 (0) = 1, % 2 (0) = 1.

Случай 3. Нулевое положение равновесия системы (1) – центр.

Получены следующие оценки параметров 6 1 ,0 2 ,0₃,0 4 :

01 = 0.072 74, 02 = 4.01077, 03 = -3.98702, 04 = -0.02925 .

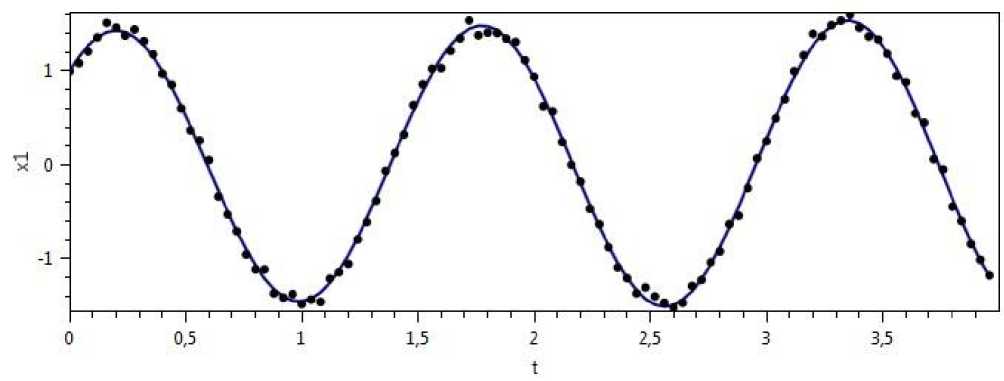
Рис. 7. Экспериментальные данные и график компоненты x 1 (t, 0) приближенного решения системы (1).

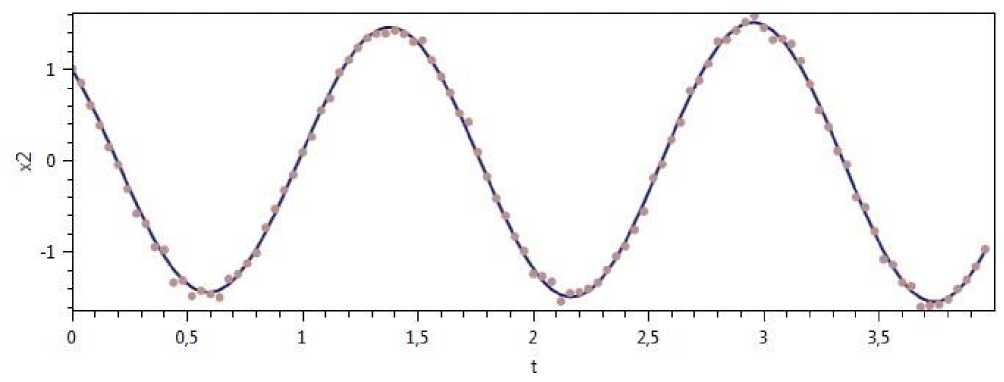
Рис. 8. Экспериментальные данные и график компоненты x2(t, 0) приближенного решения системы (1).

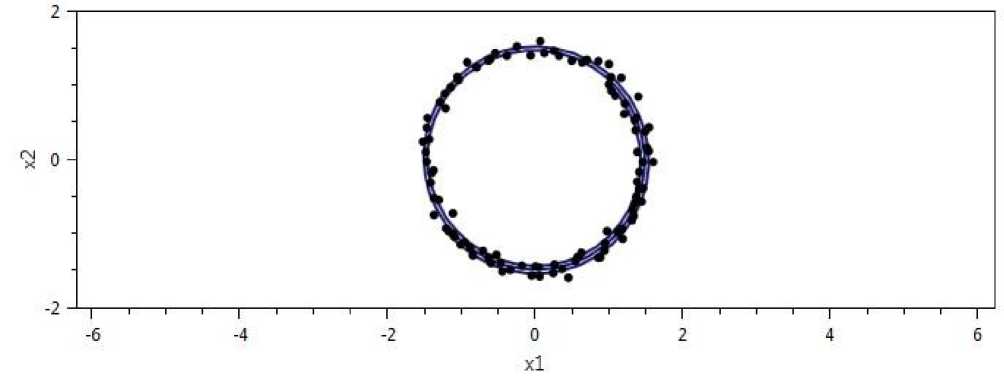
Рис. 9. Экспериментальные данные и приближение фазовой траектории системы (1).