Алгоритм энергосберегающего управления тепловым режимом здания в условиях неопределенности

Взаимодействие теплового режима жилого здания с окружающей средой можно рассмотреть как взаимодействия двух подсистем: подсистемы «внешняя среда» (наружная температура, скорость и направление ветра, солнечная радиация) и подсистемы «тепловой режим здания» [1].

На входе подсистемы «тепловой режим здания» наряду с управляемыми входными параметрами (расход теплоносителя, интегрированная температура помещений, температура в обратном трубопроводе) присутствуют и неуправляемые параметры (внутренние тепловыделения, потери тепла через ограждающие конструкции, теплота, затраченная на подогрев вентиляционного воздуха и др.), которые являются случайными. Управление тепловым режимом здания в таких условиях неопределенности является сложной задачей. Одним из вариантов решения данной проблемы является разработка оптимальной стратегии управления тепловым режимом здания, которая пригодна для большинства ситуаций. Задача нахождения такой оптимальной стратегии формализована и решается с применением аппарата теории игр [2].

1. Задача нахождения оптимальной стратегии управления тепловым режимом здания в условиях неопределенности

Алгоритм энергосберегающего управления тепловым режимом здания в условиях неопределенности и структурная схема функционирования энергосберегающей автоматизированной системы разработаны на основе методов теории игр. Эффективность управления системой теплопотребле-ния в условиях неопределенности определяется по критерию:

J* =тахм| (р(«, ),ху) |,             (1)

где U - множество допустимых значений управляемых параметров системы теплопотребления при фиксированном векторе параметров внешней среды х_;; М - символ математического ожидания.

У подсистем «внешняя среда - теплопотреб-ление» в каждой текущей ситуации имеется возможность принять одно из многих конечных состояний Sx и ST соответственно. Благодаря этому каждую текущую ситуацию задаем прямоугольной матрицей А размера п х т, где и - число стратегий (состояний) подсистемы «внешней среды» Sx, т - число стратегий подсистемы параметров ST. В матрице А существует элемент со, являющийся седловым при использовании страте гий S^ и 8'Т. Смешанную стратегию «внешней среды» 8Х описываем и-мерным вектором Sx =(Yh72>—, Y„), где Yy ~ вероятность использования чистой стратегии Sx. Смешанную стратегию подсистемы 8’т задаем /и-мерным вектором 8Т = (Л] = Й2> —’ Л™), гДе Л/ - вероятность использования чистой стратегии Sj (использование при текущем векторе «внешней среды» х z-й модели теплового режима здания.

Матрица оценок |ру|| оптимальных эффективностей управления СТП (системой теплопотребления) при использовании моделей ц, и j-ro вектора «внешней среды» х, в текущих ситуациях СТП формируется при условии, что

ЗЦ:Уу| p;(w,),x7|eO7,               (2)

где Dj - область качества управления СТП при использовании модели ц,.

Действие неконтролируемых возмущений вызывает необходимость уточнения значений матрицы ||jy||. Для этого определяются такие значения параметров U*, при которых выполняется условие

= _ max Jy { p,(w,),xj, (3)

где Зу - уточненное значение элементов Jy с учетом действия неконтролируемых возмущений.

Векторы 8_Х и Sj являются оптимальными стратегиями при условиях:

2Л/⁼^ ^Y, = 1, ^S^S-y j>со> q>^S_x,S_rУ

/=1            /=1 '

8_Т > 0, S_x > 0.

Совокупность |5^,^,coj является решением задачи оптимизации «внешняя среда - СТП» в условиях случайного изменения вектора «внешней среды» х_р точка cp^S^.S^j подчиняется цепочке неравенств:

Ф^х^г)^ ^^_Х,8_Т^ > ф(5^ ,S_T) и является седловой точкой функции /                тп п

/=1 ./=1

при условии (13), а со - значение этой функции в седловой точке.

Определяем смешанные (оптимальных) стратегий S_x и S_T, при которых гарантированное значение эффективности управления СТП

о* = sup inf фр^бу) = inf зирфр^,^).

у n V ' Я у X '

В текущих ситуациях СТП смешанная стратегия подсистемы «внешняя среда» известна, а подсистема «режим СТП» минимизирует средние потери и реализует чистую стратегию S_T = U.

• 2.    Разработка структуры энергосберегающего управления системой теплопотребления здания в условиях неопределенности

Алгоритмическая структура функционирования энергосберегающей АСУ ТП здания в условиях неопределенности (см. рисунок) предусматривает взаимосвязь между подсистемами - «внешняя среда» - «СТП» - «система коммерческого учета» - «АСУ - ТП» (автоматизированная система управления теплопотреблением) - ДПР (лицо, принимающее решение) и представляет интерактивную систему управления.

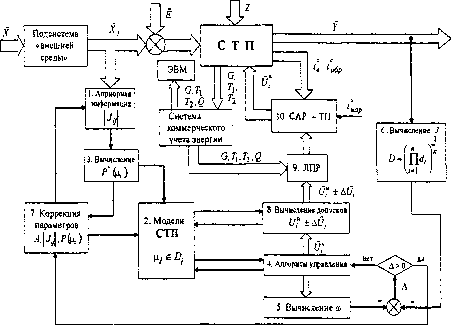
Структура энергосберегающего управления системой теплопотребления здания в условиях неопределенности

Гарантированное значение эффективности управления процессом теплопотребления в условиях неопределенности определяется на основе применения аппарата теории игр.

В терминах теории игр задача формулируется следующим образом: в игре участвуют две подсистемы - подсистема «внешняя среда» (партнер С) и подсистема теплопотребления (партнер К). В подсистеме теплопотребления может быть выбран любой (в пределах ограничений на эффективность управления тепловым режимом) режим управления (стратегии К); в подсистеме «внешняя среда» - любое (из возможных) сочетание метеопараметров (партнер С). Каждой комбинации стратегий К и С отвечает определенное значение выходного параметра процесса управления уу, который вы ступает в роли параметра оптимизации. Ограничим число возможных вариантов Ки С в пределах плана эксперимента, которые могут принимать подсистемы внешней среды и теплового режима здания, конечными числами п и т соответственно. В случае, когда пит достаточно большие числа, такое квантование вполне соответствует реальным условиям управления тепловым режимом.

В результате приходим к парной игре п х т. Так как у_у (/ = 1, 2,..., m; j = 1, 2,..., п) известны для любого сочетания К, и С_;, то игра полностью определена. Решением (за подсистему К) является смешанная стратегия, которая при многократном повторении обеспечивает наилучшее среднее значение параметра оптимизации.

Описанный подход использован для оптимизации управления тепловым режимом здания. Параметром оптимизации служила обобщенная функция желательности [3]. В качестве стратегий К рассмотрены 4 режима регулирования расхода воды (от 2 до 3,5 м³/ч), в качестве стратегий С - 84 вариантов возможных сочетаний параметров внешней среды X. Таким образом, матрица игры имела размер 4x84.

Оптимальная стратегия находилась методом итераций. Решением данной игры является активная стратегия Кд = 3,5 м³/ч. При этом цена игры равна D* = 0,617 . Таким образом, при любых сочетаниях параметров внешней среды (в пределах экспериментальных значений), эффективность управления тепловым режимом здания будет не ниже 0,617, что соответствует хорошему качеству теплового режима по шкале критерия оптимальности в виде функции желательности.

Заключение

Рассмотренный метод применяется для абонентских тепловых пунктов зданий, оснащенных теплосчетчиками, но не оснащенных средствами автоматики, и позволяет научно обоснованно устанавливать расход сетевой воды в системе отопления.