Алгоритм юстировки составных зеркал

Современное развитие технологий по созданию телескопов направлено на создание крупногабаритных зеркально-линзовых телескопов (КЗСТ). Проблемами создания КЗСТ является уменьшение поверхностной плотности главного зеркала как основного массогабаритного компонента оптической системы телескопа и массогабаритные ограничения, накладываемые как технологическими трудностями, так и системой доставки КЗСТ в космос. Учитывая, что, как правило, отражающая поверхность зеркал КЗСТ – это обычные поверхности второго порядка (1), обладающие симметрией вращения относительно оси, проходящей через его вершину, то решение этих проблем достигается, в частности, применением технологии облегчённых зеркал, позволяющей создавать главные зеркала телескопов с приемлемым значением поверхностной плотности отражающей поверхности.

В формуле (1) в соответствии с рис. 1 приняты следующие обозначения: x и y – текущие координаты в системе координат XYZ ; R x и R y – радиусы кривизны в плоскостях XOZ и YOZ ; C X и C Y – константы [ISO10110-12:1996(Е)].

Z (X, y ) =

оптической синхронизации следует выполнять двухэтапную процедуру геометрического и оптотехнического позиционирования зеркальных сегментов СЗ относительно расчётной базовой поверхности (БП).

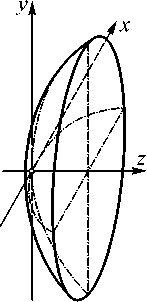
Рис. 1. Профиль отражающей поверхности зеркала

1. Теоретические основы

Современные информационные технологии, а также

технические достижения существующих актуаторов (например, пьезопривод) позволяют выполнить процесс двухэтапной юстировки методом компарирования. При этом пространственное положение сегментов СЗ относительно БП определяется касательной плоскостью к

< = <

x ²/ R x + y ²/ R_y

,

вершине отражающей поверхности сегмента и норма-

¹+ _A¹ - ( 1 ⁺ K

Kx = Rx / c_x - 1; K = R / C y - 1. x xX y yY

В силу технологических и массогабаритных ограничений для создания зеркал для крупногабаритных

лью к ней, которые пересекаются в идеальном случае в одной точке на оптической оси СЗ (ось OZ ). Уравнение касательной плоскости к точке O i (вершина поверхности i- го зеркального сегмента) и уравнение нормали к ней представлены формулами (2) и (3)

( z — zcni ) = (d z/dxcni )x( X — xcni ) + (2) + (dz/dycnt )x(y — ycni),

телескопов в последнее время применяют технологию составных отражающих поверхностей [1 –5]. Однако даже в случае изготовления зеркальных сегментов составного зеркала (СЗ) с идеальной поверхностью всё равно остаётся проблема оптической синхронизации сегментов с целью, чтобы СЗ было эквивалентно несоставному [6]. Для решения проблемы

⁽ z z cni ) = ^{( X} x cni ) = ⁽ y y cni )

^{— 1}        ( d z / d x cni )   ( d z / d y cni ) ,

[ O cni X cni ^x O cni Y cni ] i = 1 ^{x x} [ ⁰БШ^ХEni ^{x O}БПi^YБПi ] i = 1 = 0.

^A x  ^{ x eni

x cni } | ; ^A Y   ^{ yem

} m

1 ,

^A Z ^{( Z}R 0 БП

Z en ) •

Условием правильного геометрического позиционирования зеркального сегмента является то, что вектора O _{СП i}Z _{СП i} и O _{БП i}Z _{БП i} должны быть коллинеарны и пересекаться в одной расчётной точке на оси OZ (для сферической БП это центр её кривизны), а соответственно, и касательные плоскости X СПi Y СПi и X БПi Y БПi также коллинеарны. Таким образом, математическая модель, отражающая условие (5), может быть представлена в виде векторного произведения (4), а оценка точности геометрического позиционирования – соотношением (5).

• 2.    Алгоритмы позиционирования Геометрическое позиционирование

В основе геометрического позиционирования зеркальных сегментов относительно расчётной базовой поверхности лежит алгоритм последовательной технической и метрологической реализации модели 4: 1) начало геометрического позиционирования;

• 2)    исходные данные от ЭВМ: уравнение расчётной поверхности (РП). Разбиение РП на сегменты { ЗC _{РП i} } ₁ ^m . Координаты вершин, уравнения касательных плоскостей и нормалей для { ЗC _{РП i} } ₁ ^m относительно БП. Последовательность позиционирования реальных зеркальных сегментов { РЗC_i } ₁ ^m (траектория обхода);

• 3)    задают i = 1;

• 4)    устанавливают РЗС 1 в 1-ю ячейку БП, соответствующую параметрам ЗС РП 1 ;

• 5)    определяют с помощью датчиков координаты вершины, параметры касательной плоскости и нормали РЗС 1 относительно БП;

• 6)    вычисляют невязку параметров позиционирования РЗС 1 относительно параметров ЗС РП 1 ;

• 7)    если величина координатной невязки РЗС 1 не превышает допустимых величин A x , A y 1 и A z 1 , то задаются i =2. Если величина невязки превышает допустимую величину, то возвращаются в п. 4 и корректируют параметры позиционирования РЗС 1 на величину превышения допуска с помощью актуаторов этого сегмента;

• 8)    устанавливают РЗС 2 во 2-ю ячейку БП, соответствующую параметрам ЗС РП 2 ;

• 9)    определяют с помощью датчиков координаты вершины, параметры касательной плоскости и нормали A X ₁ , A _{Y 1} и A _{Z 1} относительно БП;

• 10)    вычисляют невязку параметров позиционирования РЗС 2 относительно параметров ЗС РП 1 ;

• 11)    если величина координатной невязки РЗС 2 не превышает A x 1 , A y 1 и A z 1 , то задают i = 2. Если величина невязки РЗС 2 превышает допустимую величину, то возвращаются в п. 8 и корректируют параметры её позиционирования на величину превышения допуска с помощью актуаторов этого сегмента;

• 12)    выполняют операции для РЗС 3 вплоть до РЗС m ; 13) переходят к выполнению алгоритма оптотехнического позиционирования { РЗC_i } ₁ ^m на БП.

Если выполняется условие обеспечения допуска на разность координат (5), то переходят к выполнению алгоритма оптотехнического позиционирования зеркальных сегментов относительно расчётной базовой поверхности.

Известно, что при падении на зеркало плоской волны профиль отражённой волны повторяет профиль его отражающей поверхности, тем самым условием правильного оптотехнического позиционирования зеркального сегмента относительно БП является минимизация разности волновых фронтов (6), т.е.

⁽ WEnRO  Wen RO) V   ^J    ^ ^{0.               (6)}

^{X                             0} g enR 0 i ^° g enR 0 i

В этой связи уравнение разностной поверхности Z 0 m ) ( x , y ) относительно сферы сравнения радиусом R СФ , являющееся математической моделью оптотехнического позиционирования, примет вид [7]:

Z 0 m ) ( x , y ) = 0

R _СФ

V

x БПi

I

1 + . 1 -

⁺ yen, __________

Л 2       2 A^

I ^ХБП! ^{+ y} БП! I

V RcФ ■ c J J

N (7)

x 2_n / R + y 2 / R

СПi    xi      СПi    yi

.

1 N

)[ n i =1

N

■ = max, i=1

- апертурные углы , бп -го и i en -

Технологическая карта, являющаяся технической реализацией (4), определяется технологическим и метрологическим обеспечением процесса в соответствии с алгоритмом оптотехнического позиционирования:

• 1)    начало оптотехнического позиционирования;

• 2)    исходные данные от ЭВМ: расчетные значения волновых аберраций { δ _Xi } ₁ ^m и { δ _Yi } ₁ ^m для { ЗC _{РП i} } ₁ ^m . Уравнение поверхности волновых аберраций для { ЗC РПi } 1 ^m ;

• 3)    задают i = 1;

• 4)    определяют значения волновой аберрации δ X 1 ( РЗС 1 ) и δ Y 1 ( РЗС 1 );

• 5)   вычисляют невязку [ δ X 1 – δ X 1 ( РЗС 1 )]

и [ δ Y 1 – δ Y 1 ( РЗС 1 )];

• 6)    если [ δ X 1 – δ X 1 ( РЗС 1 )] ≤ ∆ δ X 1

и [ δ Y 1 – δ Y 1 ( РЗС 1 )] ≤ ∆ δ Y 1 , то переходят к i =2. Если [ δ X 1 – δ X 1 ( РЗС 1 )] >  ∆ δ X 1 и [ δ Y 1 – δ Y 1 ( РЗС 1 )] > ∆ δ Y 1 , то возвращают в п.4 и корректируются параметры позиционирования РЗС 1 на величину превышения допуска с помощью актуаторов этого сегмента;

• 7)    определяют значение волновой аберрации δ X 2 ( РЗС 2 ) и δ Y 2 ( РЗС 2 );

• 8)  вычисляют невязку [ δ X 2 – δ X 2 ( РЗС 2 )]

и [ δ Y 2 – δ Y 2 ( РЗС 2 )];

• 9)   если [ δ X 2 – δ X 2 ( РЗС 2 )] ≤ ∆ δ X 2

и [ δ Y 2 – δ Y 2 ( РЗС 2 )] ≤ ∆ δ Y 2 , то переходят к I =2. Если [ δ X 2 – δ X 2 ( РЗС 2 )] >  ∆ δ X 2 и [ δ Y 2 – δ Y 2 ( РЗС 2 )] >  ∆ δ Y 2 , то возвращаются в п.4 и корректируют параметры позиционирования РЗС 2 на величину превышения допуска с помощью актуаторов сегмента РЗС 2 ;

• 10)    выполняют операции для РЗС 3 вплоть до РЗС m .

На рис. 2 представлены интерференционные картины поверхности сегментированного зеркала, при этом на рис. 2 а – в результате выполнения алгоритма геометрического позиционирования, а на рис. 2 б – в результате выполнения оптотехнического позиционирования (один сегмент оставлен для сравнения).

Заключение

Таким образом, разработан алгоритм геометрического и оптотехнического позиционирования зеркальных сегментов составного зеркала относительно базовой (расчетной) поверхности, отличающийся более корректной формой, чем в [8, 9].

Этот алгоритм позволяет выполнять юстировку методом виртуального компарирования, что особенно важно для режима эксплуатации высокоапертурных телескопов, работающих в автономном режиме.

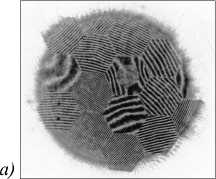
Рис. 2. Интерференционные картины поверхности сегментированного зеркала (негатив): в результате

выполнения алгоритма геометрического позиционирования (а), в результате выполнения оптотехнического позиционирования (б) (один сегмент оставлен для сравнения)