Алгоритм кластеризации элементов распределенной системы хранения конфиденциальных данных

Современные информационные системы включают в свой состав базы данных (далее – БД), информация в которые поступает от значительного количества клиентов системы, обрабатывается, а результаты обработки предоставляются клиентам в форме различных информационных сервисов.

Такие БД обычно размещаются в центрах обработки данных (далее – ЦОД), гарантирующих высокие показатели целостности, доступности и конфиденциальности.

Несмотря на то, что в штатных условиях эксплуатации ЦОД обеспечиваются требуемые значения показателей качества хранения информации, возможны кризисные ситуации (природные катаклизмы, техногенные катастрофы, террористические акты, компьютерные атаки и др.), которые неизбежно приводят к разрушению ЦОД. Поэтому БД резервируются на нескольких ЦОД, размещаясь на элементах распределенной системы хранения данных (далее – СХД).

При этом повышение доступности данных обеспечивается дублированием элементов СХД, на которых они размещаются, что гарантирует доступ к данным при отказе отдельных элементов, а конфиденциальность данных обеспечивается минимизацией их объема, хранящегося на одном элементе СХД, что снижает риск несанкционированного доступа к большому объему информации.

Отсюда возникает оптимизационная задача размещения БД (ее частей) по элементам распределенной СХД с учетом доступности и конфиденциальности хранимой информации, что позволяет в случае разрушения восстановить информацию в новом ЦОД.

Басыров Александр Геннадьевич доктор технических наук, профессор, профессор кафедры информационно-вычислительных систем и сетей, Военно-космическая академия имени А.Ф. Можайского, Санкт-Петербург. Сфера научных интересов: информационные вычислительные системы, высокопроизводительная обработка информации. Автор более 160 опубликованных научных работ. SPIN-код: 54170218, AuthorID: 540797.

Постановка задачи кластеризации элементов распределенной системы хранения данных

Будем считать, что элементы распределенной СХД взаимодействуют через сеть в интересах информационного обмена. Среди этих элементов можно выделить (назначить) главный элемент, который способен в течение установленного срока собрать данные со всех элементов в свою локальную БД. Каждый элемент может оказаться временно или постоянно в неработоспособном состоянии (поломка, отсутствие доступа в сеть и др.) [1].

В целях обеспечения возможности оперативного сбора данных необходимо резервирование их размещения на нескольких элементах СХД путем репликации одинаковых данных. Увеличение количества резервных элементов повышает вероятность доступа к данным за установленное время, однако ограничивает объем хранимых данных и повышает риск несанкционированного доступа к ним, то есть риск потери конфиденциальности данных.

Таким образом, из множества элементов распределенной СХД создаются группы элементов (кластеров), причем данные исходной БД разделяются на части, каждая из которых размещается на одном кластере. Все элементы одного кластера хранят одинаковую информацию. Пример размещения информации на СХД, состоящей из 10 элементов, представлен на Рисунке.

Количественно оценить конфиденциальность данных через вероятность несанкционированного доступа к ним – весьма непростая задача. Однако логичным является снижение угрозы несанкционированного доступа к данным с уменьшением их объема на одном элементе СХД, так как успешный несанкционированный сбор данных со множества распределенных элементов СХД всегда менее вероятен, чем с одного. При этом несомненна важность принятия стандартных мер по защите информации на каждом элементе СХД.

Алгоритм кластеризации элементов распределенной системы хранения конфиденциальных ...

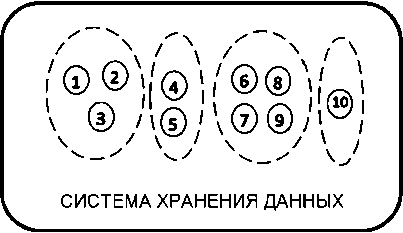
Рисунок. Пример кластеризации 10 элементов СХД Источник: рисунок выполнен авторами.

Таким образом, возникает противоречие между конфиденциальностью и доступностью данных, разрешение которого приводит к задаче формирования кластеров (кластеризации) элементов распределенной СХД, обеспечивающей возможность восстановления (сбора) данных за установленное время с учетом требований к конфиденциальности хранимых данных.

Содержательная постановка задачи заключается в формировании из множества распределенных элементов СХД максимального количества непересекающихся подмножеств (кластеров), каждый из которых обладает требуемой доступностью.

Математическая постановка задачи

Дано:

распределенная СХД, состоящая из множества E = { e 1 ,e 2 ,..,e n } взаимосвязанных элементов, n – количество элементов;

вектор D = d 1 , d 2 ,.., d n значений доступности каждого элемента СХД, где d i - вероятность получения доступа к данным, хранящимся на i -м элементе СХД, в течение установленного срока.

Найти:

разбиение множества E на непересекающиеся подмножества С 1 , C 2 ,..C m , где C i е E , m - количество подмножеств (кластеров) такое, что m ^ max при d ( C i ) > d ^m? , V i = 1,..., m , где d ( C i ) - значение доступности i -го кластера, d ^mp - директивная (требуемая) доступность каждого кластера.

Задача относится к классу задач комбинаторной оптимизации и имеет экспоненциальную сложность.

Алгоритмы субоптимальной кластеризации элементов распределенной системы хранения данных

Для решения поставленной задачи в реальных условиях (при достаточно большом количестве элементов СХД) требуются алгоритмы приемлемой сложности, обеспечивающие получение результата за ограниченное время.

Рассмотрим субоптимальный алгоритм, который формирует кластеры на основе генерации сочетаний из элементов СХД с проверкой удовлетворения кластера требуемому уровню доступности. Сочетания генерируются с возрастанием количества элементов в них. При формировании очередного кластера элементы СХД, попавшие в него, исключаются из общего множества элементов, что последовательно сокращает потенциальное количество сочетаний.

Несмотря на то что алгоритм перебирает значительное количество вариантов кластеров, в подавляющем большинстве случаев это количество значительно меньше, чем при полном переборе.

Алгоритм 1. Ограниченный перебор сочетаний элементов СХД.

Шаг 1. Начало.

Шаг 2. m : = 1 .

Шаг 3. Сгенерировать очередное сочетание C из n по m .

Шаг 4. Определить доступность d ( C ) очередного сочетания C из n по m :

m d (C)=1 -П(1 - d )• i =1

Шаг 5. Если d (C )> dm, то включить элементы сочетания C в очередной искомый кла- стер, исключить из рассмотрения элементы СХД, входящие в это сочетание, n := n - m.

Шаг 6. Если сочетание C последнее из рассматриваемых, то m := m+1 , переход на шаг 7, иначе – на шаг 3.

Шаг 7. Если m >  n , то переход на шаг 8, иначе - на шаг 3.

Шаг 8. Конец.

Процедуры ускоренной генерации сочетаний из n элементов множества по m рассмотрены во многих работах, например, в [2].

Следует отметить, что вычислительная сложность алгоритма сильно зависит не только от количества элементов в СХД, но и от значений показателя их доступности.

Отметим также, что опытным путем установлена целесообразность перед началом работы предложенного алгоритма упорядочить элементы СХД по невозрастанию значений показателей их доступности.

Рассмотрим «быстрый» алгоритм, который формирует кластеры из упорядоченных по невозрастанию значений доступности элементов СХД по следующему принципу. В очередной кластер включаются первый и несколько последних элементов СХД, количество которых определяется требуемым коэффициентом доступности кластера.

Достоинством алгоритма является его невысокая полиномиальная сложность O ( n ² ) , недостатком – меньшее по сравнению с оптимальным алгоритмом количество формируемых кластеров.

Алгоритм 2. «Быстрый» алгоритм кластеризации элементов СХД.

Шаг 1. Начало.

Шаг 2. Упорядочение элементов СХД по невозрастанию готовности.

Шаг 3. а : = 0 , ® : = n , i : = 0 .

Шаг 4. i : = i + 1 .

Шаг 5. а : = а + 1 .

Шаг 6. Создать кортеж C i : = а .

Шаг 7. x : = d a .

Шаг 8. Если x >  d^mp , то переход на шаг 4.

Шаг 9. C i : = C i о ® .

Шаг 10. x : = x + d ® - x ■ d ® .

Алгоритм кластеризации элементов распределенной системы хранения конфиденциальных ...

Шаг 11. а : = а - 1 .

Шаг 12. Если а >  а , то переход на шаг 14.

Шаг 13. Если x >  d^mp , то переход на шаг 4, иначе - на шаг 9.

Шаг 14. Конец.

В результате работы алгоритма будет создано i кортежей, соответствующих кластерам из элементов СХД, каждый из которых содержит номера элементов, входящих в соответствующий кластер.

Отметим, что вычислительная сложность алгоритма не зависит от значений показателя доступности элементов СХД.

Показателями качества рассмотренных алгоритмов являются вычислительная сложность и результативность – количество формируемых кластеров, которое целесообразно оценивать относительно оптимального значения.

Каждый из двух рассмотренных алгоритмов обладает достоинствами и недостатками. Переборный алгоритм (Алгоритм 1) характеризуется высокой трудоемкостью, но дает результат, наиболее близкий к оптимальному. «Быстрый» алгоритм, наоборот, обладает невысокой вычислительной сложностью, но менее точен.

Ниже представлен комбинированный алгоритм, в котором реализован подход совмещения двух отмеченных выше алгоритмов, что дает относительно высокую точность формирования кластеров при удовлетворительной вычислительной сложности. Принцип работы алгоритма заключается в выполнении двух этапов. На первом этапе с помощью Алгоритма 1 формируются кластеры, состоящие из 1, 2, 3 …, m элементов СХД, а оставшиеся n – m элементы СХД группируются в кластеры Алгоритмом 2. Переход от трудоемкого Алгоритма 1 к менее точному Алгоритму 2 определяется задаваемым пороговым значением m , определяющим общую трудоемкость комбинированного алгоритма.

Алгоритм 3. Комбинированный алгоритм кластеризации элементов СХД.

Шаг 1. Начало.

Шаг 2. Упорядочение элементов СХД по невозрастанию их готовности.

Шаг 3. Ввести количество ^ элементов СХД, в пределах которого будет применен алгоритм перебора сочетаний элементов СХД (выбирается, исходя из ограничений на время работы алгоритма).

Шаг 13. Выполнить Алгоритм 1 для C m сочетаний, где m <  ^ .

Шаг 13. Если ^ <  n , то выполнить Алгоритм 2 для оставшихся нераспределенными элементов СХД, иначе – переход на шаг 6.

Шаг 6. Конец.

Имитационная модель кластеризации элементов распределенной системы хранения данных

В качестве исходных данных для предлагаемого алгоритма будем использовать результаты, полученные в ходе реализации нижеприведенного алгоритма.

Алгоритм 4. Алгоритм псевдооптимальной генерации m кластеров из n элементов СХД.

Шаг 1. Начало.

Шаг 2. b : = n / m , z : = n - n : = b , k : = 0 .

Шаг 3. i : = 1 .

Шаг 4. Если i >  z , то а : = b , иначе - а : = b + 1 .

Шаг 5. d : = 1 - d ^m , x : = ^ d , p : = 1 .

Шаг 6. j : = 1 .

Шаг 7. k : = k + 1 ,

Шаг 8. Если j нечетное, то y : = d + ( 1 — d ) ■ r , d k : = d■ y , иначе - d k : = d / y . (Здесь r - случайное число из диапазона [0,1].)

Шаг 9. p : = p ■ d_k , d_k : = d_k — 1 .

Шаг 10. j : = j + 1 . Если j >  a , то переход на шаг 11, иначе - на шаг 7.

Шаг 11. d_k : = 1 — (1 — d_k ) ■ d / p .

Шаг 12. i : = i + 1 . Если i >  m , то переход на шаг 13, иначе - на шаг 4.

Шаг 13. Вывести массив D.

Шаг 14. Конец.

В результате работы алгоритма формируется массив D значений доступности элементов СХД, который можно использовать в качестве исходных данных для анализа работы алгоритмов кластеризации СХД.

Для исследования предложенного алгоритма была разработана имитационная модель [3], суть которой заключается в многократном повторении циклов генерации исходных данных (Алгоритм 4) и формировании на основе этих данных кластеров элементов СХД. В завершении каждого цикла накапливается разница между «оптимальным» количеством кластеров и количеством, полученным с помощью исследуемого алгоритма.

Алгоритм 5. Алгоритм имитационного моделирования кластеризации элементов СХД.

Шаг 1. Начало.

Шаг 2. Ввод исходных данных: n – количество элементов СХД, m – количество элементов в кластере СХД, d^oS - требуемая доступность кластера, з - количество прогонов модели.

Шаг 3. i : = 1 , 5 1 : = 0 , s ₂ : = 0 .

Шаг 4. Формирование набора кластеров алгоритмом 4 с вектором D = d 1 , d ₂ ,.., d n доступности каждого элемента СХД.

Шаг 5. Кластеризация элементов СХД комбинированным алгоритмом кластеризации (Алгоритм 3) с формированием ^ кластеров.

Шаг 6. s 1 : = s 1 + ^ — m ; s ₂ : = s ₂ + ( ^ — m ) 2 .

Шаг 7. i : = i + 1 . Если i <  п , то переход на шаг 4, иначе - на шаг 8.

Шаг 8. s : = 51/ п ; ^ : = I—— s ² .

\ п

Шаг 9. Конец.

В результате работы алгоритма переменная s будет содержать среднее значение погрешности комбинированного алгоритма кластеризации элементов СХД, а переменная а - ее среднеквадратическое отклонение.

По результатам имитационного моделирования (Алгоритм 5) с использованием исходных данных о готовности элементов СХД, полученных путем псевдооптимальной ге-

Алгоритм кластеризации элементов распределенной системы хранения конфиденциальных ...

нерации кластеров (Алгоритм 4), было установлено, что предложенный алгоритм позволяет осуществлять кластеризацию элементов СХД с достаточно хорошей точностью за приемлемое время.

Моделирование проводилось на стандартном персональном компьютере для 100 элементов СХД с оптимальным значением количества кластеров от 5 до 50, требуемой готовностью каждого кластера не менее 0,95 и ограничением на время кластеризации в 1 минуту.

Результаты моделирования представлены в Таблице.

Таблица

Результаты имитационного моделирования по кластеризации элементов СХД

Оптимальное количество кластеров	5	10	15	20	30	40	50
Среднее значение полученного количества кластеров	4	9	13,15	18,62	29	39	50
СКО полученного количества кластеров	0	0	0,36	0,49	0	0	0

Заключение

Анализ проведенных исследований показывает, что предложенный алгоритм кластеризации дает вполне удовлетворительный результат за приемлемое время работы. Рассмотренные алгоритмы с успехом могут быть применены для синтеза кластеров из отдельных элементов СХД, для которых известны значения показателя их готовности.

При несложной модификации алгоритмов возможно их применение для кластеризации и по другим показателям качества.