Алгоритм математического измерения степени зависимости переживания одиночества от внутренних и внешних факторов

Современные условия развития нашего общества предполагают переоценку многих аспектов мировоззренческого и теоретико-познавательного рассмотрения проблемы формирования человека, организацию его жизненного пространства, переживаний, связанных с экзистенциальной проблематикой. Феномен одиночества – один из наиболее серьезных социальных вопросов современности. За последние годы наблюдается прогрессирующая тенденция к расширению социальных и возрастных границ личного одиночества.

Описание научной проблемы целесообразно начать с констатации факта о том, что, благодаря усилиям ученых разных поколений, прочным достоянием психологической науки стало положение: переживание одиночества индивидами – это результат комбинированного воздействия внутренних и внешних факторов. Параллельно неустанно велись поиски адекватных методов измерения величины такого воздействия.

Например, И.Г. Циммерман говорил: «Побуждение к общежитию гораздо сильнее (здесь и далее выделено нами. — Е.К. ), чем побуждение к уединению» [Циммерман, 1781, с. 35]. Г.С. Салливан: «Одиночество впервые появляется в юности. Однако когда оно действительно наступает, то сила его уже велика» [Салливан, 1999, с. 346]. Р.С. Вейс: «Разведенные и овдовевшие люди старшего возраста склонны реже считать себя одинокими, чем разведенные и овдовевшие молодые люди» [Вейс, 1989, с. 119]. Батарея цитат свидетельствует: процесс измерения пока не вышел за рамки лексических форм и выражений, дающих довольно смутное представление о степени зависимости одиночества от внутренних и внешних факторов и лишь приблизительно описывающих степень различия.

Между тем созрели необходимые условия для перехода от приблизительных вербальных к точным математическим методам. Так, в 1920-е гг. англичанин Рональд Фишер ввел в научный оборот математический метод, предназначенный для сопоставления двух рядов выборочных значений по частоте встречаемости какого-либо 146

признака [Fisher, 1925]. В 1970-е гг. американец Даниэль Рассел разработал шкалу одиночества UCLA [Рассел, 1989]. Впоследствии она была модифицирована М. Фергюсоном [Райгородский, 2004, с. 77, 78]. В конце 1990-х гг. японец Хийджиро Тсуйи в русле биполярного подхода к «большой пятерке» предложил компактный и удобный в обращении вариант личностного опросника [Tsuji, 1998]. Однако пока эти научные методы не нашли широкого применения за пределами «своих» исследовательских направлений: статистики, лонлинологии и персонологии.

Цель и одновременно научная новизна настоящей статьи состоят в том, чтобы попытаться разомкнуть междисциплинарные рамки, синтезировать нуклеарно развивающиеся научные разработки и на основе такой интеграции получить принципиально новый продукт. Средством достижения цели является впервые вводимый в оборот алгоритм. Под последним в научно-справочной литературе принято понимать «конечный набор правил, позволяющих чисто механически решать любую конкретную задачу…» [СЭС, 1981, с. 36]. Применительно к проблеме, вынесенной в название статьи, наш алгоритм измерения включает в себя следующие структурные элементы. 1. Использование перфорационной карты респондента. 2. Введение в исследовательскую практику интегрального потенциала переживания одиночества. 3. Новации в применении модифицированной шкалы одиночества. 4. Новации в трактовке критерия Фишера – φ эмп . Рассмотрим элементы алгоритма в предложенной последовательности.

Использование перфорационной карты респондента (ПКР). Стандартизированная ПКР представляет из себя картонный прямоугольник с перфорацией по двум сторонам и срезанным верхним левым углом. Ее образец представлен на рис.

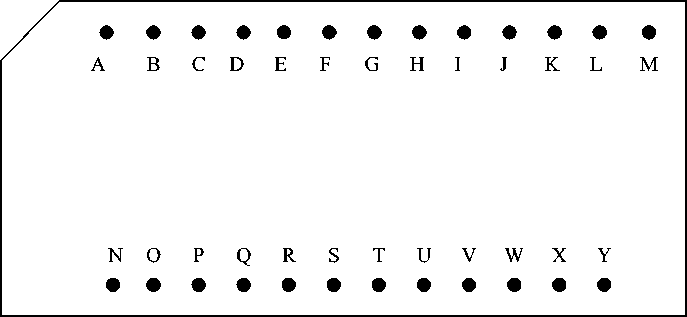
Рис. Образец стандартизированной перфорационной карты респондента

Условные обозначения: A – низкий уровень ПО; B – средний уровень ПО; C – высокий уровень ПО; D – экстраверсия; E – интроверсия; F – привязанность; G – отделённость; H – контролирование; I – естественность; J – эмоциональность; K – эмоциональная сдержанность;

L – игривость; M – практичность; N – мужчина; O – женщина; P – младший; Q – старший; R – женат / замужем; S – холост / не замужем; T – проживает дома; U – проживает вне дома; V – горожанин; W – селянин; X – «технарь»; Y – гуманитарий

Одна ПКР соответствует одному сброшюрованному протоколу, включающему в себя модифицированную шкалу одиночества Д. Рассела и М. Фергюсона, пятифакторный опросник Х. Тсуйи, социально-демографическую анкету, разработанную автором статьи. Содержание этих методик проанализировано в одной из наших публикаций [Яблокова, 2009]. В соответствующих местах карты делаются прорези, соединяющие ее кромку с перфорационным отверстием. Эти прорези в сочетании с вязальной спицей и обрезанным углом позволили унифицировать процесс класси- фикации и систематизации массива эмпирических данных по всевозможным лон-линолого-персонологическим и лонлинолого-социодемографическим ракурсам и основаниям.

В ходе заполнения каждой карты происходит процесс перевода качественных показателей в количественные, которые лежат в основе последующих элементов алгоритма. Цифра, обозначающая сумму баллов по шкале одиночества, является своеобразным «генетическим кодом» испытуемого и фигурирует в качестве базовой при многочисленных и разнообразных вычислениях, группировках и перегруппировках массы карточек. Каждая ПКР представляет из себя емкую информационную матрицу. Взятые в совокупности они реально помогают выявить всевозможные разнообразные количественные параметры связей и отношений, сложившиеся между феноменом одиночества, с одной стороны, внешними и внутренними факторами – с другой.

Введение в исследовательский оборот интегрального потенциала переживания одиночества (ИППО). Психологическая сущность этого элемента алгоритма заключается в суммировании (интеграции) баллов ПО, набранных всеми (без исключения) респондентами той или иной независимой выборки. Итоговая цифра, выраженная в баллах ПО, – это и есть показатель интегрального потенциала переживания одиночества.

Однако показатель ИППО важен не сам по себе, а только в сопоставлении с показателем численности участников выборки. При этом сравниваются между собой не только абсолютные числа, но и их процентные доли. Всего сформировано одиннадцать пар независимых выборок. Их список приведен в расшифровке «условных обозначений», приложенной к перфокарте. В качестве примера возьмем из перечня первую пару (экстраверсия – интроверсия) и последнюю («технари» – гуманитарии) (табл. 1).

Таблица 1

Сравнение выборок респондентов и интегральных потенциалов ПО

№ п / п	Пары независимых выборок	Респонденты и баллы ПО		В % к итогу в диаде по вертикали		Уровни значимости
		Респонденты	Баллы ИППО	Респонденты	Баллы ИППО	φ эмп
1	Экстравертные	182	2483	89,2	85,0	1,64
2	Интровертные	22	439	10,8	15,0	0,57
...
21	«Технари»	104	1175	50,0	39,6	2,04
22	Гуманитарии	104	1789	50,0	60,4	2,07

Третий и четвертый столбцы таблицы содержат необходимые относительные данные. Основная идея ИППО кроется в возможности сопоставления двух соседних цифр, расположенных по горизонтали. Пока «журча еще бежит за мельницу ручей», жернова вертятся и мука мелется. Пока между соответствующими процентными долями существует «перепад высот», эвристический потенциал присутствует. Если же показатели удельных весов выборок числа респондентов и баллов ИППО идентичны, то перспективы изучения феномена одиночества приближаются к нулю. (Про последний столбец будет сказано позднее.) Введение в научный оборот ИППО позволяет «заловить» и зафиксировать тонкие нюансы проявления зависимости переживания одиночества от внутренних и внешних факторов. Этот новый измерительный инструмент не отменяет традиционный, а гармонично дополняет его в зависимости от специфики решаемой исследовательской задачи.

Новации в применении модифицированной шкалы одиночества. Изначально последняя предназначалась главным образом для выявления пациентов, обладающих высоким уровнем переживания одиночества, с последующим проведением психотерапевтической и / или психокоррекционной работы. Наши респонденты – современные студенты-дневники – априори далеки от высокого уровня ПО. Малая абсолютная и относительная численность таких испытуемых (например, у нас: n=4, или 1,9 %) выводит последних из круга величин, к которым применим статистический метод сравнения. Чтобы не терять из виду этих интересных во многих отношениях респондентов и в то же время сохранить возможность применения необходимых математических процедур, объединили с группой испытуемых среднего уровня ПО. Вновь образованной независимой выборке, где n=47, или 22,6 %, присвоено наименование «испытуемые со средневысоким уровнем переживания одиночества», или «СВ уровень ПО». Это первая новация.

Объективная сложность интерпретации результатов исследования обусловила необходимость использования вербальных ярлыков. При этом важно учитывать разницу и не допускать смешения понятий «конструкт» и «вербальный ярлык». Например, «неодинокий индивид» или «одинокий индивид» – это вербальные ярлыки, а «респондент с низким уровнем переживания одиночества» и «респондент со средневысоким уровнем переживания одиночества» – это конструкты. Такова вторая новация.

Разработка и применение третьей новации продиктованы спецификой исследования. О чем конкретно идет речь, наглядное представление дают данные табл. 2 и 3. В них столбцы n 1 и n 2 содержат количественные параметры выборок респондентов соответственно: с низким (неодинокие) и средневысоким (одинокие) уровнями ПО. В качестве примера из перечня факторов взяты уже ставшие привычными диады: экстравертные – интровертные, «технари» – гуманитарии.

При сравнении обеих таблиц отчетливо видно: они едины и одновременно противоположны друг другу. Обе содержат одинаковые абсолютные величины и неодинаковые – относительные. Сопоставление и анализ «горизонтальных» и «вертикальных» количественных данных позволяют полнее и глубже раскрыть и исследовать спектр математических, а затем и психологических связей и отношений, царящих между внутренними и внешними факторами, с одной стороны, и феноменом переживания одиночества – с другой. Все сказанное здесь в равной мере относится и к табл. 1. О заключительных столбцах, как и в первом случае, речь ниже.

Таблица 2

Сравнение выборок респондентов по личностным качествам и вузовским специальностям в контексте уровней ПО

Пары независимых выборок	Выборки		В % к итогу в диаде по горизонтали		Уровни значимости
	n1	n2	n1	n2	φ эмп 1	φ эмп 2
Экстравертные	147	35	80,8	19,2	1,91	1,60
Интровертные	12	10	54,5	45,4
«Технари»	91	13	87,5	12,5	3,25	1,58
Гуманитарии	70	34	67,3	33,7

Таблица 3

Сравнение выборок респондентов по уровням ПО в контексте личностных качеств и вузовской специальности

Пары независимых выборок	Выборки		В % к итогу в диаде по вертикали		Уровни значимости
	n1	n2	n1	n2	φ эмп
Экстравертные	147	35	92,5	77,8	2,37
Интровертные	12	10	7,5	22,2	1,02
«Технари»	91	13	56,5	27,7	2,00
Гуманитарии	70	34	43,5	72,3	2,84

Новации в трактовке критерия Фишера – φ эмп . Указанный статистический метод «оценивает достоверность различий между процентными данными двух выборок, в которых зарегистрирован интересующий нас эффект» [Сидоренко, 2006, с. 158]. В трех приведенных выше таблицах в правых столбцах сосредоточены колонки цифр, отображающие эмпирическое значение уровней статистической значимости для независимых выборок. Способ исчисления критерия Фишера – φ эмп хорошо освещен в специальной литературе [Сидоренко, 2006]. Остается лишь напомнить, что критическое значение φ , соответствующее принятому в психологии уровню статистической значимости, имеет следующие параметры:

_φ= 1,64 (р ≤ 0,05) φ кр = \ 2,28 (р ≤ 0,01).

Иными словами, если коэффициент значимости равен или больше 1,64, то различие между двумя независимыми выборками считается статистически значимым, т. к. подтверждается в 95 случаях из 100. Если коэффициент равен или больше 2,28, то различие считается статистически высокозначимым, т. к. подтверждается в 99 случаях из 100.

В «статаналитических» столбцах трех приведенных таблиц содержится полный спектр уровней различия: незначимый (4 коэффициента), значимый (5), высокозначимый (3). Мы полагаем: каждый из них – это своеобразная флеш-карта, в которой в свернутом виде закодирована квинтэссенция информации о содержании, структурных связях и отношениях, сложившихся между лонлинологической областью, с одной стороны, и биполярными конструктами в факторных сферах – с другой. Сердцевиной, сущностью этой системы связей и отношений является феномен переживания одиночества. В то же время значение совокупности математических коэффициентов можно сравнить с внедренными в неоднородную, подвижную среду монолитными сваями, на которые опирается ажурная конструкция психологической интерпретации. Это наша первая новация в трактовке. Вторая – вытекает из первой.

В целях оптимизации исследования, а также для сохранения разумного соотношения между математическими и психологическими началами желательна кардинальная перекомпоновка имеющегося в наличии массива коэффициентов. Последние сортируются в соответствии с одним биполярным конструктом и становятся тем самым связаны друг с другом осмысленным образом (контекстом) аналогично ролям в пьесе.

Перекомпоновка состоит и в том, чтобы числовые значения критерия Фишера были расположены по принципу убывания своей величины. В каждой конструк-тной диаде первым стоит компонент ведущий, а вторым – ведомый. Все это помогает определить, какие актеры в нашей пьесе играют главную роль, какие – роль второго плана, а какие – статиста. Наглядным примером сказанного служат данные следующих двух таблиц.

Таблица 4

Сравнение выборок по конструкту экстраверсия – интроверсия

Пары выборок	φ эмп
Неодинокие экстравертные и одинокие экстравертные	2,37хх
Неодинокие экстравертные и неодинокие интровертные	1,91х
Экстравертные и ИППО экстравертными	1,64х
Одинокие интровертные и одинокие экстравертные	1,60
Одинокие интровертные и неодинокие интровертные	1,02
ИППО интровертными и интровертные	0,57

Таблица 5

Сравнение выборок по конструкту «технари» – гуманитарии

Пары выборок	φ эмп
Неодинокие «технари» и неодинокие гуманитарии	3,25хх
Одинокие гуманитарии и неодинокие гуманитарии	2,84хх
ИППО гуманитариями и гуманитарии	2,07х
«Технари» и ИППО «технарями»	2,04х
Неодинокие «технари» и одинокие «технари»	2,00х
Одинокие гуманитарии и одинокие «технари»	1,58