Алгоритм метода перемещений с параметрическим изменением внешних силового и кинематического воздействий
Автор: Ловцов А.Д., Костюнина О.А.
Журнал: Вестник Восточно-Сибирского государственного университета технологий и управления @vestnik-esstu
Статья в выпуске: 1 (36), 2012 года.
Бесплатный доступ
Задача идеального контакта деформируемых тел сведена к линейной задаче дополнительности (ЛЗД) в терминах взаимных перемещений контактирующих тел и контактной матрицы жесткости. Предложена модификация алгоритма Лемке, в которой параметр расширения задачи физически представляет собой изменение внешнего воздействия.
Строительная механика, метод перемещений, односторонние связи, линейная задача дополнительности, метод лемке
Короткий адрес: https://sciup.org/142142423
IDR: 142142423 | УДК: 539.3
Текст научной статьи Алгоритм метода перемещений с параметрическим изменением внешних силового и кинематического воздействий
К системам с односторонними связями относятся конструкции, части которых односторонне взаимодействуют одна с другой, либо в их составе есть элементы, работающие только на растяжение или сжатие.
Расчетные (рабочие) схемы систем с односторонними связями зависят от величины и характера внешнего воздействия. В связи с этим появляется необходимость в определении действительного состояния данных связей (включены – выключены), т. е. в определении рабочей схемы конструкции. В пределах одной рабочей схемы система остается линейной. Целью настоящей работы является отслеживание последовательности смены рабочих схем при простом загружении конструкции силовой и кинематической нагрузками.
Задача расчета систем с идеальными (без учета трения) односторонними связями после дискретизации сводится к условной задаче квадратичного программирования [1]:
П (z) = — zTRz - zTR F ^ min,
2 (1)
z > 0.
Здесь z – взаимное перемещение контактных пар точек по направлению односторонних связей; R – контактная матрица жесткости; R F – вектор сил взаимодействия контактных пар точек по направлению односторонних связей от заданной нагрузки (грузовой вектор). Перемещения принято считать положительными Z i > 0 , если они не ограничиваются односторонней связью.
Обозначим ~ = z + п , где П — вектор известных обобщенных зазоров по направлению z, и запишем условия Куна-Таккера для задачи (1):
~
1) x = R ~ + R F ; 2) x > 0; 3) ~ > 0; 4) ~ Tx = 0,
~ где x - вектор сил взаимодействия контактных пар точек; RF = RF - Rn.
Система уравнений 1, условий неотрицательности 2, 3 и условий дополняющей нежесткости 4 из (2) представляют собой линейную задачу дополнительности (ЛЗД) [3, 4]. Алгоритм решения данной задачи можно интерпретировать как метод перемещений строительной механики с применением терминов: основная система метода перемещений, единичные состояния (дислокации); взаимные перемещения контактных пар точек; контактная матрица жесткости и т. п.
Для решения задачи (2) предлагается алгоритм с параметрическим изменением внешнего воздействия, являющийся модификацией алгоритма Лемке [3, 4]. При параметрическом изменении внешнего воздействия R F = pR V +R C, где pR V , R C – изменяющаяся и постоянная составляющие внешнего воздействия; p – параметр изменения внешнего воздействия. Тогда ЛЗД (2), расширенная введением параметра p , перепишется в виде:
1) x - R~ - pR V = R C ; 2) x > 0; 3) ~ > 0; 4) ~ T x = 0; 5) p > 0. (3)
Расширенная задача (3) будет эквивалентна исходной задаче (2) при p = 1.
Ясно, что только одна переменная из каждой пары xi , zi в силу 2) – 4) из (3) будет отлична от нуля. Условие 4) из (3) устанавливает правило дополняющей нежесткости для определения индекса переменной, вводимой в базис. А именно в базис вводится переменная, взаимодополнительная к переменной, вышедшей из базиса. Если из базиса вышла (стала равной нулю) переменная xi (что соответствует выключению связи в контактной паре i – «момент отрыва»), то в базис должна войти переменная zi , определяющая взаимное удаление точек контактной пары i . Если из базиса вышла переменная zi (включение связи, «момент касания»), то в базис, естественно, войдет xi – сила взаимодействия вступивших в контакт точек.
Проиллюстрируем применение предлагаемого алгоритма решения задачи (3) на примере задачи одностороннего контакта балки с шарнирно-неподвижной опорой у левого конца и тремя дискретными жесткими односторонними опорами, работающими только на сжатие (рис. 1 а ). Между балкой и односторонней опорой 2 предусмотрен зазор величиной 1 мм. Требуется при заданном смещении опоры отследить смену рабочих схем конструкции при действии внешнего воздействия.
Основная система метода перемещений выбирается превращением всех односторонних связей в двусторонние. Это позволяет сформировать контактную матрицу жесткости и грузовой вектор. При этом контактирующие тела в основной системе сомкнуты один с другим без зазоров, тем самым создается предварительное напряжение основной системы замкнутыми зазорами.
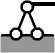
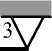
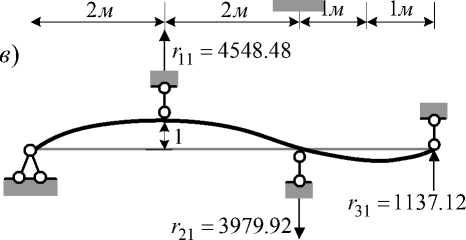
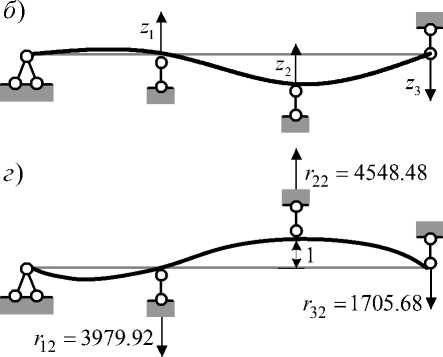
Компоненты контактной матрицы жесткости R представляют собой реакции во введенных связях от «единичных» дислокаций опор 1, 2, 3 (рис. 1 а , в , г , д ). С целью определения значений этих компонент построены «единичные» эпюры M 1 , M 2 , M 3 (рис. 1 е , ж , з ).
Балка загружена двумя сосредоточенными силами F 1 и F 2 . Силы прикладываются к конструкции поочередно: нагрузка F возрастает до значения 2,5 кН , затем при действующей силе F 1 = 2,5 кН начинает возрастать нагрузка F 2 до значения 7,5 кН .
Грузовой вектор метода перемещений формируется из реакций во введенных связях основной системы от заданной нагрузки. С целью формирования грузовых векторов R F1 и R F2 построены эпюры M 01 и M 02 соответственно от сил F 1 и F 2 (рис. 1 и , к ).
В результате имеем:
|
" 4548.48 -3979.92 -1137.12 " |
'- 0 . 375 |
' 1 . 125 ' |
' 0 1 |
||||
|
R = |
-3979.92 4548.48 1705.68 |
, R F 1 = ' |
1 . 813 |
- , R F 2 =' |
- 5 . 44 |
- , з = ■ |
0 . 001 |
|
-1137.12 1705.68 758.08 |
. - 1 |
. 3 |
. 0 |
а)
I M 20

F 1 = 2.5 кН
' Г
1 мм
2 F 2
Основная сиситема
= 7.5 кН
д )
F. = 1705.68 r = 1137.12
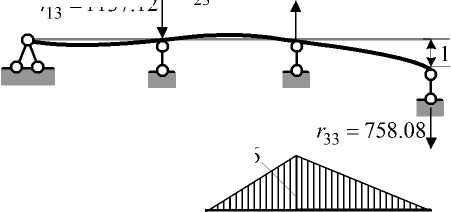
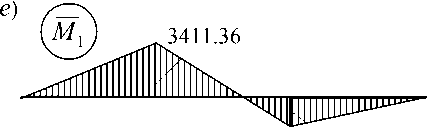
2274.24
3411.36
2274.24
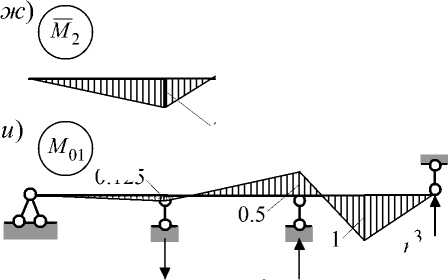
0.125
r F1 = 0.375 F = 1.813
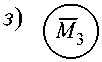
1516.16
r F 1 = 1
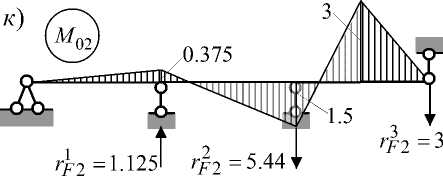
Рис. 1
На первом этапе алгоритма снимаем преднапряжение основной системы метода перемещений, вызванное замкнутыми зазорами, т. е. полагаем RV = 0, что означает отсутствие силовой нагрузки. Ис- пользуя алгоритм с искусственно введенным обжатием [2], формируем начальную таблицу ЛЗД и про-< 3,98 )
изводим расчет конструкции на воздействие R C = — R n =
- 4,549
(— 1,706 )
Грузовые векторы R F1 и R F2 располагаются в разных столбцах и преобразуются вместе со всей таблицей в результате выполнения шагов алгоритма на этапе I.
Таблица 1
Начальная таблица этапа I
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
— R3 |
|
x1 |
1 |
0 |
0 |
-4548,5 |
3979,9 |
1137,1 |
-1 |
-0,375 |
1,125 |
3,98 |
|
x2 |
0 |
1 |
0 |
3979,9 |
-4548,5 |
-1705,7 |
-1 |
1,813 |
-5,438 |
-4,549 |
|
x3 |
0 |
0 |
1 |
1137,1 |
-1705,7 |
-758,08 |
-1 |
-1,0001 |
3,0004 |
-1,706 |
Базисное решение x i = 3 . 98 , x 2 = - 4 . 549 , Х 3 = - 1 . 706 недопустимо из-за нарушения переменными x 2 и x 3 условия неотрицательности [4]. Для решения ЛЗД на шаге 1 в базис следует ввести параметр p1 такой, чтобы все базисные переменные оказались большими нуля. Физически это означает введение в опорных сечениях такой прижимающей силы p1 (одинаковой для всех опор), которая для одной из опор обеспечит «момент отрыва».
В результате выполнения шага 1 имеем следующее.
Таблица 2
Шаг 1
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
- Кз |
min |
|
x1 |
1 |
-1 |
0 |
-8528,4 |
8528,4 |
2842,8 |
0 |
-2,1876 |
6,563 |
8,5284 |
0,001 |
|
p1 |
0 |
-1 |
0 |
-3979,9 |
4548,48 |
1705,68 |
1 |
-1,8126 |
5,438 |
4,5485 |
0,001 |
|
x3 |
0 |
-1 |
1 |
-2842,8 |
2842,8 |
947,6 |
0 |
-2,8128 |
8,4383 |
2,8428 |
0,001 |
Базисные переменные: x i = 8 . 528 , pl = 4 . 549 , Х 3 = 2 . 843 . Величина обжатия pl такова, что деформированная балка отрывается от опоры 2 (рис. 2 а ). Поскольку из базиса вышла переменная x 2 , то на следующем шаге согласно правилу дополняющей нежесткости x 2 • z 2 = 0 в базис должна войти переменная z 2 . Для выбора ведущей строки воспользуемся правилом минимального отношения. Поскольку величина отношения одинакова во всех трех случаях, выбираем ведущую строку так, чтобы переменная p1 вышла из базиса, и проводим шаг однократного замещения Жордана-Гаусса. В результате имеем следующее.
Таблица 3
Шаг 2
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
- Кз |
|
x1 |
1 |
0,875 |
0 |
-1066 |
0 |
-355,35 |
-1,875 |
1,211 |
-3,633 |
0 |
|
z2 |
0 |
-0,0002 |
0 |
-0,875 |
1 |
0,375 |
0,0002 |
-0,0004 |
0,0012 |
0,001 |
|
x3 |
0 |
-0,375 |
1 |
-355,4 |
0 |
-118,45 |
-0,625 |
-1,6799 |
5,0397 |
0 |
Базисное решение: x i = 0 , z 2 = 0 . 001 м , x 3 = 0 . Полученный результат показывает, что смещение односторонней опоры 2 вертикально вниз и, следовательно, выключение ее из работы при отсутствии внешней нагрузки не влияет на напряженное состояние балки.
Параметр обжатия pl вышел из базиса. Следовательно, pl = 0 и этап I завершен (рис 2 б).
На втором этапе решаем ЛЗД с R C = - R n( I 1 и R V = R F 11 1 1 . Начальная таблица этапа II получается из таблицы, соответствующей концу первого этапа. Векторы R F /11 и R F2W переносятся влево за знак равенства с противоположным знаком. Параметр p2 характеризуют изменение внешней силовой нагрузки F 1 . Параметр p3 на данном этапе считается равным 0 в связи с отсутствием силового воздействия F 2 .
Таблица 4
Начальная таблица этапа II
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
- Кз $ |
min |
|
x1 |
1 |
0,875 |
0 |
-1066 |
0 |
-355,4 |
-1,875 |
-1,211 |
3,6332 |
0 |
|
|
z2 |
0 |
-0,0002 |
0 |
-0,875 |
1 |
0,375 |
0,0002 |
0,0004 |
-0,001 |
0,001 |
2,5093 |
|
x3 |
0 |
-0,375 |
1 |
-355,4 |
0 |
-118,5 |
-0,625 |
1,6799 |
-5,04 |
0 |
0,0000 |
При p2 = 0 базисное решение: x i = 0 , z 2 = 0 . 001 м , Х 3 = 0 , что соответствует отсутствию силовой нагрузки. Для начала итерационного процесса вводим в базис параметр нагрузки p2 (таким образом, ведущий столбец соответствует p2 ). По правилу минимального отношения определяем номер ведущей строки и проводим шаг однократного замещения Жордана-Гаусса. В результате получим следующее.
Таблица 5
Шаг 3
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
- R3 $ |
min |
|
x1 |
1 |
0,6047 |
0,721 |
-1322 |
0 |
-440,7 |
-2,326 |
0 |
0 |
0 |
|
|
z2 |
0 |
-0,0001 |
-0,0002 |
-0,791 |
1 |
0,4031 |
0,0004 |
0 |
0 |
0,001 |
0,002 |
|
p2 |
0 |
-0,223 |
0,595 |
-211,5 |
0 |
-70,51 |
-0,372 |
1 |
-3 |
0 |
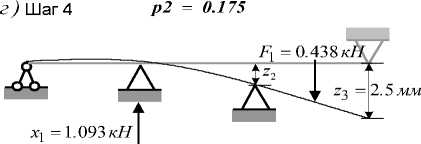
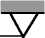
В таблицах 6-8 (этап II: шаги 4 – 6) показано выполнение шагов алгоритма с параметрическим изменением нагрузки F 1 . На рисунке 2 в , г , д , е представлены рабочие схемы, соответствующие каждому шагу алгоритма.
Таблица 6
Шаг 4
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
- R3 $ |
min |
|
x1 |
1 |
0,4615 |
0,4615 |
-2186,8 |
1093,4 |
0 |
-1,9231 |
0 |
0 |
1,0934 |
2,37 |
|
z3 |
0 |
-0,0003 |
-0,0006 |
-1,9616 |
2,4808 |
1 |
0,0009 |
0 |
0 |
0,0025 |
|
|
p2 |
0 |
-0,2461 |
0,5538 |
-349,84 |
174,92 |
0 |
-0,3077 |
1 |
-3 |
0,1749 |
Таблица 7
Шаг 5
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
- R3 |
min |
|
x2 |
2,1667 |
1 |
1 |
-4738 |
2369 |
0 |
-4,1667 |
0 |
0 |
2,369 |
|
|
z3 |
0,0007 |
0 |
-0,0003 |
-3,5 |
3,25 |
1 |
-0,0004 |
0 |
0 |
0,0033 |
|
|
p2 |
0,5333 |
0 |
0,79991 |
-1516 |
757,99 |
0 |
-1,3332 |
1 |
-3 |
0,758 |
Таблица 8
Шаг 6
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
- R3 |
|
x2 |
0,5 |
1 |
-1,5 |
0 |
0 |
0 |
0 |
-3,1254 |
9,376 |
0 |
|
z3 |
-0,0005 |
0 |
-0,0021 |
0 |
1,5 |
1 |
0,00264 |
-0,0023 |
0,0069 |
0,0015 |
|
z1 |
-0,0004 |
0 |
-0,0005 |
1 |
-0,5 |
0 |
0,00088 |
-0,0007 |
0,002 |
-0,0005 |
Этап II завершается получением лучевого решения (шаг 5), что означает неизменность рабочей схемы при дальнейшем увеличении параметра p2 . Чтобы выразить базисные переменные этой рабочей схемы через p2 , следует выбрать ведущую строку так, чтобы параметр p2 вышел из базиса.
Базисные переменные x 2 , z 3 , z 1 получаются вычитанием столбца, соответствующего p2 , из столбца, соответствующего - R3 ^ :
|
B = • |
f 1 2 z 3 |
> |
f 0 = 0 . 0015 |
М |
' - 3 . 125 ' - 0 . 0023 |
> = < |
3 . 125 0 . 0038 |
|
. Z 1 |
_- 0 . 0005 |
_- 0 . 0007 |
0 . 0002 |
Начальная таблица этапа III формируется из результатов, полученных по окончании этапа II, с учетом того, что R C = B и R V = R F 2 ( II > .
В таблице 9-14 (этап III: шаги 7 – 11) представлены результаты выполнения шагов алгоритма с параметрическим изменением нагрузки F 2 с учетом приложенной силы F = 2 . 5 кН . На рисунке 2 ж , з , и , к , л приведены рабочие схемы, соответствующие каждому шагу алгоритма.
Таблица 9
Начальная таблица этапа III
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
B |
min |
|
x2 |
0,5 |
1 |
-1,5 |
0 |
0 |
0 |
0 |
-3,1254 |
9,3761 |
3,1254 |
0,333 |
|
z3 |
-0,0005 |
0 |
-0,0021 |
0 |
1,5 |
1 |
0,0026 |
-0,0023 |
0,0069 |
0,0038 |
0,55 |
|
z1 |
-0,0004 |
0 |
-0,0005 |
1 |
-0,5 |
0 |
0,0009 |
-0,0007 |
0,002 |
0,0002 |
0,1 |
Таблица 10
Шаг 7
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
B |
min |
|
x2 |
2,1667 |
1 |
1 |
-4738 |
2369 |
0 |
-4,1667 |
0 |
0 |
2,369 |
1,093 |
|
z3 |
0,0007 |
0 |
-0,0003 |
-3,5001 |
3,25 |
1 |
-0,0004 |
0 |
0 |
0,0033 |
4,62 |
|
p3 |
-0,1778 |
0 |
-0,2666 |
505,328 |
-252,66 |
0 |
0,4444 |
-0,3333 |
1 |
0,0807 |
Таблица 11
Шаг 8
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
B |
min |
|
x1 |
1 |
0,4615 |
0,4615 |
-2186,8 |
1093,4 |
0 |
-1,9231 |
0 |
0 |
1,0934 |
0.001 |
|
z3 |
0 |
-0,0003 |
-0,0006 |
-1,9616 |
2,4808 |
1 |
0,0009 |
0 |
0 |
0,0025 |
0.001 |
|
p3 |
0 |
0,082 |
-0,1846 |
116,614 |
-58,307 |
0 |
0,1026 |
-0,3333 |
1 |
0,275 |
Таблица 12
Шаг 9
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
B |
min |
|
x1 |
1 |
0,6047 |
0,7209 |
-1322,2 |
0 |
-440,74 |
-2,3256 |
0 |
0 |
0 |
0 |
|
z2 |
0 |
-0,0001 |
-0,0002 |
-0,7907 |
1 |
0,4031 |
0,0004 |
0 |
0 |
0,001 |
|
|
p3 |
0 |
0,0744 |
-0,1984 |
70,511 |
0 |
23,5036 |
0,124 |
-0,3333 |
1 |
0,3333 |
Таблица 13
Шаг 10
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
B |
min |
|
x3 |
1,3871 |
0,8387 |
1 |
-1834,1 |
0 |
-611,36 |
-3,2258 |
0 |
0 |
0 |
|
|
z2 |
0,0003 |
0,00007 |
0 |
-1,2258 |
1 |
0,2581 |
-0,0004 |
0 |
0 |
0,001 |
|
|
p3 |
0,2752 |
0,2408 |
0 |
-293,42 |
0 |
-97,806 |
-0,5161 |
-0,3333 |
1 |
0,3333 |
Шаг 11
|
Базис |
x1 |
x2 |
x3 |
z1 |
z2 |
z3 |
p1 |
p2 |
p3 |
B |
|
x3 |
-0,3333 |
-0,6667 |
1 |
0 |
0 |
0 |
0 |
2,0836 |
-6,2507 |
-2,0836 |
|
z2 |
-0,0008 |
-0,0009 |
0 |
0 |
1 |
0,6667 |
0,0018 |
0,0014 |
-0,0042 |
-0,0004 |
|
z1 |
-0,0009 |
-0,0008 |
0 |
1 |
0 |
0,3333 |
0,0018 |
0,0011 |
-0,0034 |
-0,0011 |
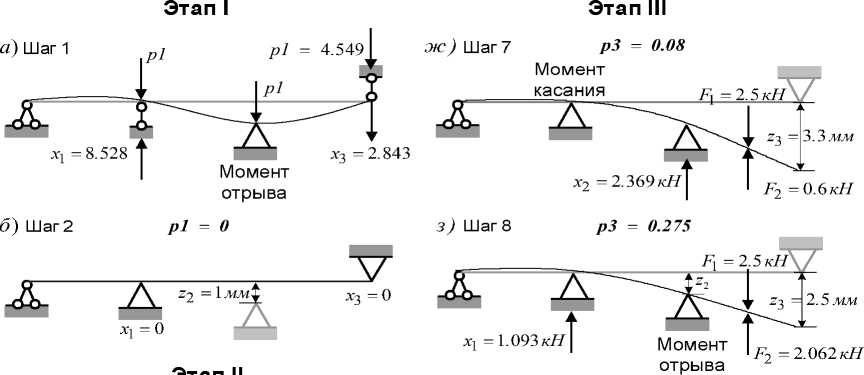
в ) ШагЗ
F 1 = 0
и) Шаг 9
p3 = 0.333
p2 = 0
z 2 = 1 мм $


Момент
отрыва

x 1 = 0
F1=2.5кН z2=1ммф '
Момент касания

2 . 5 кН
x 1 = 0
к) Шаг 10
p3 = 0.333
F 1 = 2 . 5 кН
x 3 = 0

= 1 мм
Момент

2.5кН отрыва
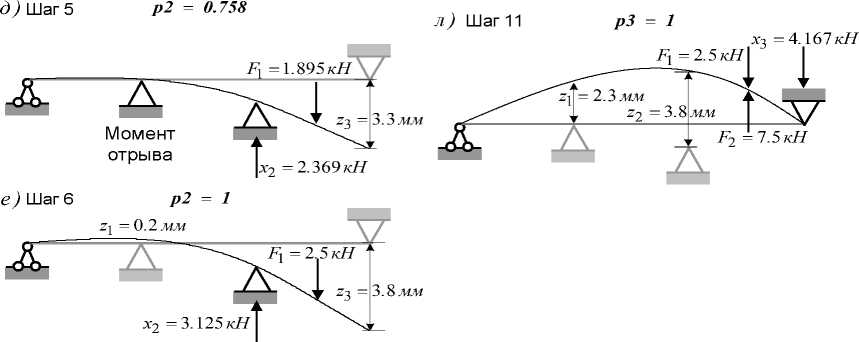
Рис. 2
Этап III также завершается получением лучевого решения (шаг 13). Значения базисных переменных x 3 , z 2 , z 1 получаются вычитанием столбца, соответствующего p3 , из столбца, соответствующего B :
|
' x 3 ' |
' - 2 . 084 ' |
' - 6 . 251 ' |
' 4 . 167 ' |
|||
|
z z 2 |
> = < |
- 0 . 0004 |
- 0 . 0042 |
> = < |
0 . 0038 |
|
|
, z |
_- 0 . 0011 |
_- 0 . 0034 |
0 . 0023 |
Таким образом, в результате произведенных расчетов установлена действительная рабочая схема конструкции, определены «включенные» и «выключенные» из работы односторонние связи, получены численные значения реакций связей от действия приложенных сил.
Заключение. Предложенный алгоритм позволяет отследить последовательность смены рабочих схем конструкции при нагружении, состоящем из нескольких этапов. Этапы нагружения могут быть как силовыми, так и кинематическими или представлять их комбинацию. Особенностью алгоритма также является его способность решать контактные задачи и в том случае, когда одно из тел может смещаться как жесткое целое.


