Алгоритм минимизации функционала, ассоциированного с задачей 3-SAT и его практические применения

Одной из наиболее интересных задач дискретной математики является задача поиска решающего набора в задаче ВЫПОЛНИМОСТЬ. После классической работы Кука [5] усилия многих исследователей были направлены на построение эвристических, переборных алгоритмов решения КНФ. Перспективным направлением представляется и сведение КНФ к непрерывному аналогу, к задаче поиска точек глобального минимума ассоциированного функционала. В данной работе обосновывается выбор функционала специального вида и предлагается применить к решению системы нелинейных алгебраических уравнений, определяющих стационарные точки функционала, модифицированный метод последовательных приближений. В работе также показано, что метод может быть с успехом применен к важным задачам криптографического анализа несимметричных шифров.

Пусть L ( x ) - пропозициональная формула в конъюнктивной нормальной форме на множестве булевых переменных x е B ^N {0,1} . Задача ВЫПОЛНИМОСТЬ (SAT) заключается в том, что бы найти решающий набор x ₀ е B ^N {0,1} , такой что

между булевыми и вещественными переменными следующее: ЛОЖЬ ^ О, ИСТИНА ^ 1.

Переход от булевой формуле к вещественной основан на использовании соответствия:

L ( x ₀) = ИСТИНА или доказать, что решающего набора не существует.

Рассмотрим переход от задачи ВЫПОЛНИМОСТЬ к задаче поиска глобального минимума функционала.

Пусть дана КНФ:

- y,v y,^ x +xj

* yt л у, ^ xixj , где {yi е B, xi е R}_yi^ (1 -xi)

Легко заметить, что min F ( x ) = 0 соответству- x е E ⁿ

M

L (x) = П

i = 1

C i , где C i - дизъюнкты вида

ет достижению значения ИСТИНА на исходной КНФ.

Без потери общности можно рассмотреть 3-ДНФ, эквивалентную исходной КНФ:

ci = U qi j (xj) • Здесь qi j (xj) = xj или xj j < N

Сделаем переход к эквивалентной ДНФ:

M

L = L ( x ) = U C i , где C i- - конъюнкты вида i = 1

Ci = П Qi,j (xj). Здесь Qi,j (xj ) = qi ,j(xj )

j <  N

Рассмотрим функционал вида:

M

minF(x) = ZCi(x)’ где x е E               i=1

N

Ci( x)=П Qi, j(xj), где j=1

J ( ^x ) = Z ^z i jl , где

S

1 - xi , если xt е ci (x)

zi = *               —

xi       , если xi е ci (x)

Здесь c i ( x ) — i триплет

Дифференцируя функционал по всем переменным x_i , получаем систему уравнений:

Zzjz2xi- = ZzV2, i =1»2»..P, где

5еВ

S\

= ^{{ S} , iE ^S : ^x i E ^c i ( ^{x ) }}

(          -- ) или

'(1 — xj )2 , если xj 2 — xj , если xj 1 ,иначе е Ci(x)

е Ci( x)

Л = {S, i е S : xi е ci (x)}

A(x1,••, xi—1, xi+1,.. xn ) ■ x = Bi(x1,••, xi—1, xi+1,.. xn ),

i = 1,.. P

Коэффициенты A и B связаны соотношением:

A i^{( x} 1

,.., xi—1, xi+1,..xn ) > Bi (x,,.., xi—, , xi+1,..x„ )

Суммирование ведется по всем M конъюнктам ДНФ, эквивалентной исходной КНФ. Соответствие

Поясним выбор представления исходной КНФ именно в виде эквивалентной 3-ДНФ. Дифференцируя функционал F ( x ) (1) по всем переменным x i ,

получаем систему уравнений аналогичную (3), но количество вкладов в Ai и B i определятся длиной скобок. Любая процедура решения этой системы при произвольной длине скобок будет естественным образом приводить к большим ошибкам округления. Ограничивая число переменных в скобках, мы исключаем эту техническую трудность.

Рассмотрим систему (3), как нелинейное операторное уравнение:

Ф( x) = 0                                (4)

Как показано в [5] применение метода Ньютона к решению данного уравнения неэффективно, т.к. решение принадлежит ядру производного оператора. Как альтернатива был предложен метод последовательных приближений с «инерцией»[2]:

K

(Е Е apxi(t— p)2 xj(t— p)2) xk(t+о= p=0feH

Е xj(t)xk(t) ~ A • Xk (t +1) = B       (5)

f eA

K

Е ap = 1     , где  ap e ^[0,1]

p = 1

Имеется ввиду то, что итерации происходят для вещественных чисел, а итоговый или промежуточный вектор проектируется на B^N {0,1} , и уже на булевом векторе проверяется SAT. Ниже мы опишем различные модификации и гибридизации метода последовательных приближений с «инерцией» в применении к решению задачи K-SAT, и покажем способы повышения эффективности алгоритма.

Гибридизация алгоритма

Основная процедура состоит из последовательных итераций, которые совмещают метод последовательных приближений и сдвиг по антиградиенту, т.к. правая часть (3) это не что иное, как антиградиент исходного функционала.

Итерация состоит из двух блоков. Первый блок, определяется формулой (5), используется схема Зейделя. Суть схемы Зейделя в том, что при нахождении очередного x i ( t + 1) на ( t + 1) -й итерации, это значение подставляется вместо x i ( t ) . Необходимо отметить, что реализация алгоритма допускает использование схемы Якоби, когда найденные x i ( t + 1) не используются в текущей итерации. Тесты показали, что схема Зейделя более устойчива в применении к решаемой задаче. Именно, после каждой итерации по схеме Зейделя значение функционала монотонно уменьшается, чего нельзя сказать о схеме Якоби. Кроме того, во всех случаях схема Зейделя быстрее приводила к решению. Отметим, что данное обстоятельство препятствует напрашивающейся простой схеме распараллеливания процесса решения с разделением данных.

Второй блок - реализация сдвига по градиенту. Рассмотрим (4). Пусть x ( t ) является решением, тогда Ф ( x ( t )) = 0 . Уравнение (5) переписывается в виде A ( x ( t )) • x ( t ) — B ( x ( t )) = 0 . Это необходимое условие, которому должен удовлетворять вектор решения. Если текущее t -е приближение x ( t ) не является решением, то A i ( x ( t )) • x i ( t ) — B i ( x ( t )) = p i ^ 0 . Для итеративной формулы: A i ( x ( t )) • x i ( t + 1) — B i ( x ( t )) = p i . Следовательно, что бы удовлетворить необходимому условию, необходимо перейти к вектору:

x (t +1) = x( t) + pj A (6)

Очевидно, что после реализации (6) возможна ситуация, когда x ( t + 1) t ^ [0,1] . В этом случае необходимо штрафным способом ограничивать x i ( t + 1) , иначе метод начинает экспоненциально расходиться. Особенно это проявляется на K-SAT формулах при K>4. При приближении к решению скорость сходимости может сильно уменьшаться, т.е. алгоритм формирует цикл лежащий на некотором плато (поверхность, определяемая функционалом) и траектория, образованная последовательными приближениями более не выходит за пределы этого плато. Чтобы сойти с плато и продолжить сходимость к решению применяется т.н. метод смены траектории.

Метод смены траектории заключается в поиске нового вектора приближения, который бы обладал свойствами не худшими, чем текущий вектор приближения, но позволял бы продолжить поиск решения. Суть метода нахождения такого вектора в следующем.

Рассмотрим 3-КНФ, эквивалентную исходной 3-ДНФ (1):

K(x) = П (zi + zj + zk )’ где f

xt      , если x e ci (x)

z i = i                —

11 — xi , если xi e ci (x)

Здесь c i ( x ) — i триплет .

K(x) = 1 ^ (zi + zj + zk) * 0, Vf

Для данного приближения x , рассмотрим множество переменных:

E 0 = { x i | 3 триплет c i : x i или — x i e c i &  c i ( x ) = 0 } С вероятностью m_p поменяем значения x i на противоположные. При этом, вероятность того, что другие триплеты станут невыполнимыми не высока. Экспериментально установлено, что полученный вектор x 0 обладает свойствами не худшими, чем x

(количество невыполнимых триплетов до и после операции примерно одинаково). Используя данный вектор x ₀ в качестве нового начального приближения, алгоритм очень быстро (в большинстве случаев за 5-10 итераций) находит следующее приближение, на котором функционал F ( x ) достигает значения не хуже, чем на векторе x . При этом, очень часто, удается проскочить плато, но при дальнейшем движении по новой траектории метод может зациклиться на другом плато. Тогда метод смены траектории повторяется.

Дополнительно рассмотрим множество:

Введем вероятности m_p0, m_p1. С вероятностью m_p0 при смене траектории будем использовать множество E 0 . С вероятностью m_p1 – множество E 1 . Вероятность m_p0 влияет на величину изменения вектора и при этом количество невыполнимых триплетов не увеличивается. Вероятность m_p1 влияет на качественное изменение вектора, количество невыполнимых триплетов может увеличиться. В принципе, чем выше m_p1, тем меньшую роль играют рестарты. Метод смены траектории применяется при достижении условия |F( x ₂) - F ( x i )| <  8 2.

Преобразование позволяет получить КНФ с меньшим количеством дизъюнктов и литералов, эквивалентную исходной.

«Резольвента» – дизъюнкция конъюнктов, отличающихся знаком по единственной переменной. Все возможные резольвенты добавляются к КНФ и используются для вычисления других резольвент.

Дублирующие конъюнкты и тавтологии удаляются, и используется сокращенная процедура с глубиной рекурсии 1. Вычислительная сложность процедуры O ( n • log n ) . Метод резолюции в применении к КНФ, ассоциированных с задачами факторизации и дискретного логарифмирования (см. ниже) позволяет уменьшить исходное число конъюнктов до 50%.

Подробно о методе резолюций можно найти в [4]

Результаты численных экспериментов

После каждой модификации проводилось тестирование алгоритма для определения эффективности проделанных изменений. При тестировании использовалось несколько типов примеров: тесты с соревнований решателей SAT 2005 года , тесты библиотеки SATLib , тесты, сформированные для задач факторизации и дискретного логарифмирования, тесты для КНФ больших размерностей, сформированные случайным образом.

Основной результат вычислительных экспериментов относительно модифицированного метода последовательных приближений, проводившихся для случайного наполнения наборов скобок SAT и 3-SAT, представлен в [3]. При соотношении

N

0 = — < 0.5 , где N это число переменных, M чис-M ло скобок в 3-SAT (эксперименты проводились вплоть до N ~ 106, M ~ 2 • 106), итерационная процедура всегда сходится к решению. Но при увеличении 0 скорость сходимости резко падает и, хотя большинство компонент решения x формируется верно, и быстро, оставшаяся часть оказывается практически недостижимой.

Результаты - метод последовательных приближений с инерцией (+ сдвиг по градиенту)

Оказалось, что сдвиг по градиенту хорошо сокращает погрешности и ускоряет сходимость алгоритма. Вычислительные эксперименты со случайными формулами показали заметное уменьшение времени решения тестов. Число решенных примеров увеличилось примерно на 20%. Применение данного приема позволило достаточно эффективно решать тесты uf20-91 (из 1000 тестов решены 703). Однако некоторые тесты решались только после задания определенного начального приближения, что говорит о необходимости рестартов. На примерах uf250-1065 алгоритм показал результат 6% от стандартных трудных тестов (предыдущая версия алгоритма - 1%). Тесты SAT-2005 (OKGenerator10000-42000 – 10000 переменных, 42000 скобок) использовались в сокращенной форме. Максимально удалось решить подформулы из 36000 скобок (предыдущая версия алгоритма – 35000 скобок). На подформулах из более чем 36000 скобок метод зацикливается на некотором плато. Это говорит о необходимости смены траектории.

Результаты - метод последовательных приближений с инерцией (+ метод смены траектории)

Метод смены траектории существенно увеличил число решаемых примеров. Результаты представлены в таблице 1.

Увеличение разрядности вычислений

Была исследована сходимость алгоритма при увеличении разрядности вычислений. Испытания с типами DOUBLE и FLOAT показали преимущество вычислений с двойной точностью. При переходе на тип DOUBLE количество решенных примеров увеличивается на 10%, скорость сходимости в среднем также увеличивается. Дальнейшее увеличение разрядности к значимому эффекту не приводит.

Таблица 1. Результаты тестирования алгоритма + метод смены траектории

Наименование теста	Количество литералов (N)	Количество дизъюнктов (M)	Число тестов	% решенных тестов	Максимальное число итераций
Backbone-minimal Sub-instances (формулы с минимальным хребтом), 3-SAT
RTI	100	429	500	98,6	19988
BMS	100	<429	500	79,8	29831
Controlled Backbone Size Instances (b – размер хребта), 3-SAT
CBS_b10	100	403	1000	100	38972
CBS_b10	100	449	1000	100	38880
CBS_b90	100	449	1000	98	29738
Uniform Random 3-SAT (UF)
uf20-91	20	91	1000	100	448
uf250-1065	250	1065	100	98	9731
SAT-encoded "Flat" Graph Colouring Problems
flat30-60	90                     \	300	100            \	100                \	4317

В последнее время наблюдается повышенный интерес к проблеме кодирования криптографических алгоритмов в терминах задачи выполнимости (SAT). В работе [1] эскизно иллюстрируется подход, позволяющий в принципе свести задачу факторизации к SAT. Целью данного пункта статьи является построение алгоритмов генерации эквивалентных, но различных КНФ и последующей минимизации ассоциированного функционала, для задачи факторизации, задачи дискретного логарифмирования, задачи дискретного логарифмирования на эллиптической кривой.

Результаты работы алгоритма для задачи факторизации

Результаты приведены в табл. 2.

Таблица 2. Результаты тестирования полного алгоритма для задачи факторизации.

1*	2*	3*	4*	5*	6*
20 32 40 44 48 56 60 68 72	254 801 990 1199 1428 1946 2235 2873 3222	4979 17867 22333 27291 32741 45141 52079 67455 75881	0.1 с 2 м 7 м 36 м 3,5 ч 36 м 10,2ч 79 ч 168ч	0.1 с > 1 ч > 1 ч > 1 ч >10ч >10ч >20ч >100ч >200ч	0.1 с 1.8м 12 м >1 ч >10ч >10ч >20ч >100ч >200ч
1*- Число бит в факторизуемом числе 2*- Количество литералов 3*- Количество дизъюнктов 4*- Время решения методом последовательных приближений 5*- Время решения алгоритмом RANOV (победитель 2005 г.) 6*- Время решения алгоритмом SATz (один из лучших переборных алгоритмов) Знак '>' означает, что за указанное время решение найдено не было

Для группы задач длины до 72 бит факторизуемого числа были получены точные решения. При этом эффективность предложенного метода превосходит известные нам алгоритмы.

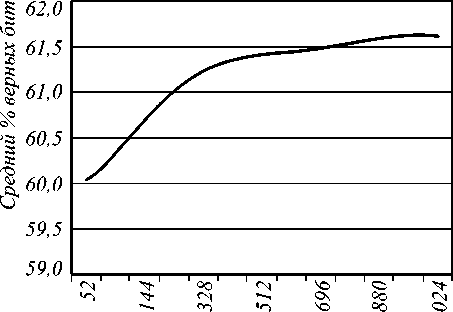
Другой интересный результат в том, что уже после первых нескольких сотен итераций метод находит более 59% верных бит решения. Трудность заключается в определении, какие именно биты были определены верно. При этом при росте числа бит исходного факторизуемого числа, происходит рост процентного отношения числа верных бит для соотношения, определяющего факторизуемое число (см. Рис. 1).

Число бит

Рис.1. Рост процентного отношения числа верных бит к числу бит факторизуемого числа.

Для тестирования использовалось 50 различных тестов для каждой размерности. В качестве сомножителей выбирались числа, удовлетворяющие всем тестам, гарантирующим криптостойкость RSA. На рисунке представлены усредненные данные. Обратим внимание на то, что вне зависимости от размерности задачи для каждого теста проводилось всего 1000 итераций. Исходя из таблицы 2 можно сделать предположение о том, что размерность 56 бит является «слабой» для алгоритма минимизации.

Рассмотрим непосредственно алгоритм сведения к КНФ задачи факторизации. Требуется для заданного числа n получить КНФ, решающий набор которой существует тогда, и только тогда когда n составное число. Кроме того, решающий набор должен содержать все биты двоичного представления нетривиальных делителей n. Без потери общности, рассмотрим классический алгоритм умножения «столбиком». Будем отождествлять биты сомножителей и результата с литералами (свободными логическими переменными). Результат умножения первого сомножителя на i-ый бит второго можно представить в виде вектора P_i . Именно суммирование всех этих векторов представляет основную сложность. Поэтому предлагается выполнять эту операцию последовательно с сохранением результата в промежуточных векторах S_k .

Весь процесс вычисления можно разбить на три этапа относительно операции сложения:

• 1)    Сложение векторов составленных из произведений двух литералов. Выполняется один раз. В результате этой операции будет заполнен вспомогательный вектор сумм S ₁ и вычислено два младших бита результата. Условно данный этап можно записать так: P 1 + P 2 = ( S ₂, r ₂, r 1 ) .

• 2)    Суммирование вектора S_k с вектором произведений. Выполняется N-3 раз. В результате заполняется массив S k _{+ 1} и вычисляется очередной бит результата

s-:+P =($„ , rJ/=э... n -1

Последнее суммирование вектора S_k с вектором произведений. Выполняется один раз. В результате вычисляются оставшиеся биты результата.

^S N - 2 ^{+ P} N = ⁽ r 2 N "  "  r N )

Теперь перейдём к рассмотрению идеи генерации КНФ. Простейший случай – приравнивание одного литерала другому: x = y . Данное равенство будет справедливо тогда и только тогда, когда истинна формула ( x V y )( x V y ) .

Другим часто встречающимся выражением является:

x = A ® B ® C                    (10)

Поступая аналогичным образом, получаем эквивалентную формулу:

(x v(A ® B® C))(x v(A ® B ® C)) =

(Ax ® Bx ® Cx ® x)(Ax ® Bx ® Cx)

Для представления правой части в виде КНФ воспользуемся леммами 1, 2.

Лемма 1.

(® x = П (xf1 V x:^1 V ^ V xN ), где в

;        {f)eMN левой части сумма по модулю 2, MN – множество двоичных векторов длины N, содержащих чётное число нулей. Операция «возведения в степень» имеет стандартный для булевой алгебры смысл:

x

x ,

x ,

5 = 0

5 = 1

Лемма 2.

N

V x ⁵ i = 1 ^;

L

VH y? =

j = 1

П { n _k } e 2 L /{ 0,0, ^ ,0 }

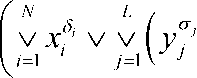
После применения леммы 1 будут получены конъюнкты следующего вида:

(^ V abc V xyc), т.е. можно выделить 3 вида дизъюнктов внутри каждого конъюнкта:

1) Одиночные литералы (то к чему следует стремиться: в правильной КНФ все дизъюнкту должны быть одиночными литералами).

Дизъюнкты вида

П x ⁵ , которые по правилу де

Моргана можно легко свести к одиночным лите- ралам.

3) Дизъюнкты вида

П^ x ⁵ , наиболее трудный

случай, сведение скобок с такими дизъюнктами к

КНФ иллюстрируется леммой 2.

Отдельного рассмотрения заслуживает операция вычисления переноса в следующий разряд при суммировании трёх слагаемых. Перенос может быть вычислен через соответствующую сумму:

c = carry (x, y, z, sum) = (sum ® xyz ® xyz

Выполнение данного равенства эквивалентно истинности следующей формулы:

sum Ф xyz Ф xyz

(c v (sum Ф xyz Ф xyz))

Приведённое выражение можно преобразовать положив: x = c , A = sum , B = xyz , C = xyz . И далее описанной выше процедурой можно построить соответствующую КНФ. Трудоемкость полученного алгоритма оценивается, как O ( n ²) в зависимости от количества бит исходного числа. Для факторизации числа, представляемого двоичным вектором длиной 1024 бит получились КНФ с 500 000 переменными 12000 000 скобок. Отметим, что результат о превышении числа верных бит после нескольких тысяч итераций алгоритма (5) относится именно к числу переменных, например, из 500 000 переменных мы получаем в среднем 300 000 верных, что в силу очевидных соотношений между битами переноса по строке, отвечающей нулевому биту, может существенно облегчить решение основной задачи.

Сведение к КНФ других задач криптоанализа

Были построены аналогичные алгоритмы сведения для задач дискретного логарифмирования и дискретного логарифмирования на эллиптической кривой. Предложен алгоритм генерации множества эквивалентных КНФ для задачи факторизации, учитывающий неделимость на малые простые числа. Последнее обстоятельство позволяет строить параллельные версии приведенных выше алгоритмов и методикой «голосования бит» определять верные биты с большой вероятностью.

Разработанный метод не уступает известным методам решения SAT на многих группах тестовых примеров и превосходит их на тестах задачи факторизации больших размерностей. Показан рост относительного числа верно найденных бит для задачи факторизации с ростом размерности задачи, так для рабочего числа бит 1024 среднее значение верных бит равно 61.75%, что больше стартового значения в 59.5% для 50 бит. Кроме того, показано наличие

«слабых» размерностей, для которых метод является эффективным. Аналогичные результаты получены и для задачи дискретного логарифмирования, но основным препятствием здесь является высокая размерность получающихся задач, так для 1024 бит число переменных в функционале оценивается величиной 10 000 000 000, а число дизъюнктов на порядок больше. Результаты точного решения КНФ, эквивалентных задаче дискретного логарифмирования приведены в таблице 3.

Таблица 3. Результаты тестирования полного алгоритма для задачи дискретного логарифмирования.

1*	2*	3*	4*	5*	6*
18 20 22 24 26	28224 38840 51832 67440 85904	448018 623239 839032 1099630 1409250	63.57 108.20 182.73 277.46 417.71	97.23 >1800 >1800 >1800 >1800	81.16 >1800 >1800 >1800 >1800
1*- Размерность, бит 2*- Количество литералов 3*- Количество дизъюнктов 4*- Время решения методом последовательных приближений, сек 5*- Время решения алгоритмом RANOV, сек (победитель 2005 г.) 6*- Время решения алгоритмом SATz, сек (один из лучших переборных алгоритмов) Знак '>' означает, что за указанное время решение найдено не было

• 1.    Беспалов Д.В. , О логических выражениях для задачи 2-ФАКТОРИЗАЦИЯ // Беспалов Д.В. Семёнов А.А.Вычислительные технологии. – 2002. – Т.7 – Ч.2.

• 2.    Файзуллин Р.Т. О решении нелинейных алгебраических систем гидравлики // Сибирский журнал индустриальной математики. -1999.-№2. –С. 176-184.

• 3.    Файзуллин Р.Т., Алгоритм минимизации функционала, ассоциированного с задачей 3-SAT и его практические применения, // Файзуллин Р.Т., Хныкин И.Г., Дулькейт В.И., Салаев Е.В.- г.Челябинск, 2007.

• 4.    Хныкин И.Г., Модификация КНФ, эквивалентных задачам криптоанализа асимметричных шифров методом резолюции // ИТМУ № 8, 2007.

• 5.    Cook S.A. The Complexity of Theorem Proving Procedures. Proceedings Third Annual ACM Symposium on Theory of Computing, May 1971.