Алгоритм моделирования поперечного сечения одномерного волокнистого продукта

Одномерным считают волокнистый продукт, образованный волокнами и/или нитями, у которого размер (длина) вдоль одной оси на много порядков больше размеров по двум другим осям, то есть размеров в плоскостях поперечных сечений [1, 2]. Несмотря на «одномерность», эти волокнистые продукты могут иметь большое число волокон и нитей в своих поперечных сечениях: от нескольких десятков для тонкой пряжи до нескольких десятков тысяч в чесальной ленте. Особенности распределения поперечных сечений волокон и нитей в поперечном сечении продукта в некоторых случаях имеет решающее значение и оказывает влияние на свойства продукта. Поэтому важно располагать алгоритмом компьютерной имитации таких поперечных сечений продукта [3‒5]. Основное упрощение, используемое в модели, ‒ это замена реальной формы поперечного сечения нити кругом, равновеликим реальному сечению нити [6-9]. Радиус круга равен r = J (T /( n q)),                  (1)

где Т - линейная плотность нити, текс, q ‒ объёмная плотность материала нити.

Такое упрощение позволяет описывать сечение каждой нити всего тремя переменными:

координатами центра (x; y) в декартовых координатах или (R; β) в полярных координатах, и радиусом равновеликого круга r . Особенность задачи геометрического моделирования поперечного сечения продукта заключается в том, что получаемая модель должна удовлетворять требованиям, делающим ее адекватной моделируемому объекту. К числу требований относятся:

• 1)    сечения нитей не должны пересекаться, но могут и должны для части нитей касаться друг друга;

• 2)    распределение нитей по толщине должно отвечать заданному распределению;

• 3)    расположение нитей в сечении должно быть частично упорядоченным. Это означает, что расположение должно соответствовать тому, которое возникает при формировании продукта, но и содержать случайную составляющую;

• 4)    при наличии в сечении смеси разнородных типов нитей, например, натурального и искусственного происхождения, алгоритм должен обеспечивать заданное распределение компонентов по площади поперечного сечения;

• 5)    форма и размеры смоделированного поперечного сечения продукта должны соответствовать заданным значениям и условиям [10-11].

Предлагаемый алгоритм моделирования основан на имитации процесса уплотнения нитей в сечении по мере формирования продукта и состоит из нескольких этапов. На первом этапе («начальная конфигурация») для каждой из N нитей сечения продукта генерируются значения {r; fi; RM}. Радиус r и угол fi генерируются в соответствии с заданными распределениями. Радиус RM в M раз больше возможного, в соответствии с его распределением, радиуса R. Множитель M выбирается настолько большим, чтобы гарантировать отсутствие пересечения нитей. Затем производится проверка условия отсутствия пересечения нитей

(х (1) - х (j)) Л 2 + (у (1) - y (j)) Л 2 > = (г (1) + г (j)) Л 2

для всех пар нитей (1; j | 1, j =1,...,N). При обнаружении хотя бы одного пересечения увеличиваем множитель M.

На втором этапе («сжатие и утруска») выполняется уменьшение всех R = RM («сжатие») и проверка условия отсутствия пересечений. При обнаружении пересечения какой-то пары нитей выполняется случайное варьирование значений R и fi для этой пары нитей («утруска») до расстояний между их центрами не меньше суммы их радиусов r. Составляющие второго этапа повторяются многократно (несколько десятков раз), до тех пор, пока они перестают давать эффект исключения пересечения нитей в сечении продукта. На этом построение геометрической модели завершается.

На рисунке 1 приведен пример работы алгоритма при геометрическом моделировании поперечного сечения одномерного волокнистого продукта, образованного одним компонентом, например, волокнами шерсти, имеющими широкое распределение тонины волокон и случайное их распределение по площади поперечного сечения. Видно, что волокна разной тонины равномерно распределены в сечении продукта как вдоль радиуса, так и по угловой координате вокруг центра сечения. Волокна плотно прилегают друг к другу, при этом сохраняя случайность расположения.

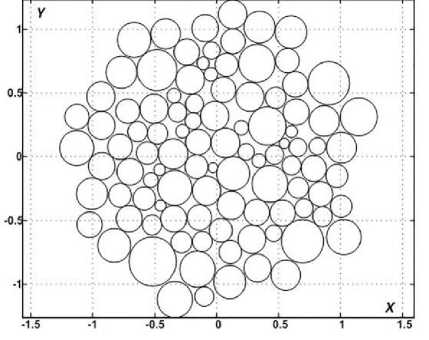
Рисунок 1 ‒ Случайное плотное распределение нитей в поперечном сечении продукта, образованного одним компонентом

На рисунке 2 приведен пример работы алгоритма для случая моделирования поперечного сечения продукта, состоящего из двух компонентов. Первый компонент - натуральные волокна с сечениями, распределенными по закону гамма-распределения. Они расположены по периферии сечения продукта. Второй компонент - нити искусственного происхождения, одинакового круглого сечения и хаотично расположенные в сердцевине сечения нити. На рисунке 3 показан пример моделирования сечения, аналогичного сечению, изображенному на рисунке 2, но с регулярной упаковкой нитей большого сечения в центре сечения, которые образуют стержень продукта. Семь таких нитей расположены строго регулярно, с соблюдением круговой симметрии. Подобные сечения характерны для комбинированной и армированной пряжи.

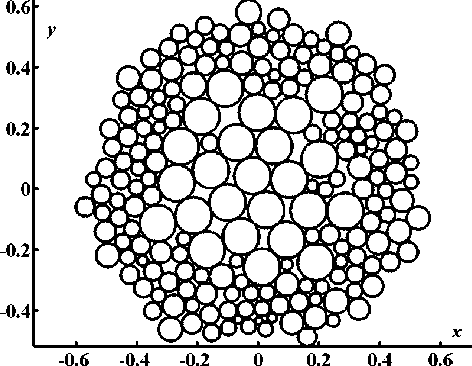
Рисунок 2 ‒ Примеры моделей сечений продукта из двух компонентов: хаотичное расположение волокон обоих компонентов, одного – в центре продукта, другого - по периферии

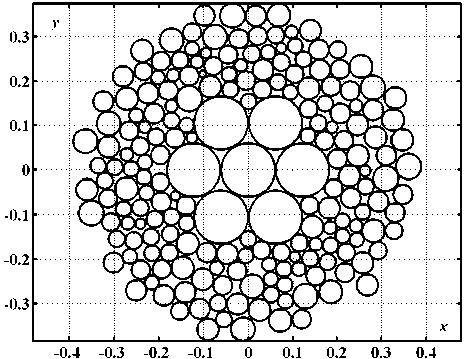
Рисунок 3 ‒ Примеры моделей сечений продукта из двух компонентов: регулярное симметричное одного компонента в центре продукта, и хаотичное – другого компонента по периферии

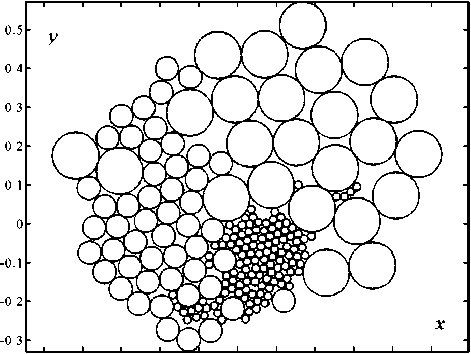
На рисунке 4 показана сгенерированная алгоритмом модель поперечного сечения продукта, образованного двумя компонентами. Один компонент, состоящий из нитей одинакового сечения, расположен регулярно и крестообразно, другой компонент, с широким распределением сечений своих нитей, хаотично заполняет свободные площади сечения продукта.

На рисунке 5 показан пример моделей сечения продукта, образованного тремя различными компонентами. Каждый из компонентов – нити постоянного сечения. Структура продукта такова, что каждый из компонентов расположен в своем секторе сечения. При этом расположение сечений нитей является хаотичным.

Приведенные примеры геометрических моделей поперечных сечений одномерного волокнистого продукта говорят о больших возможностях разработанного алгоритма. Отметим, что затраты компьютерного времени на моделирование возрастают пропорционально числу нитей в поперечном сечении и сложности структуры сечения. Это обстоятельство является важнейшим фактором, влияющим на возможности детализации модели и ее применения как составной части различных механических моделей волокнистых продуктов.

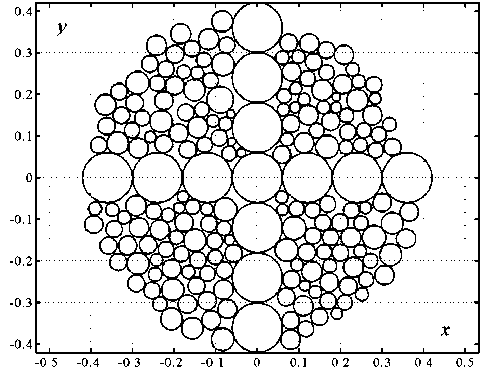
Рисунок 4 ‒ Примеры моделей сечений продукта из двух компонентов: регулярное симметричное крестообразное расположение нитей одного компонента в центре продукта, и хаотичное – другого компонента по незанятой части площади поперечного сечения

-0.5 -0.4 -0.3 -0.2 -0.1    0    0.1   0.2   0.3   0.4   0.5

Рисунок 5 ‒ Пример сечений продуктов из трех компонентов

ВЫВОДЫ

• 1.    Предложен и программно реализован алгоритм геометрического моделирования поперечного сечения одномерного волокнистого продукта, имеющего многокомпонентный волокнистый состав и заданную структуру распределения компонентов в поперечном сечении.

• 2.    Алгоритм учитывает особенности строения поперечного сечения волокнистого продукта: плотную упаковку нитей и регулярно-хаотический характер их расположения в пределах сечения вокруг центра сечения.

• 3.    Приведены примеры работ алгоритма для двух- и трехкомпонентных смесей сложной структуры.