Алгоритм начальной инициализации кватерниона пространственной ориентации в параметрах Родрига-Гамильтона

2“Stilsoft” LLC, Stavropol, Russian Federation

Введение. В задачах определения пространственной ориентации твердого тела относительно опорной системы координат широко применяются бесплатформенные инерциальные навигационные системы. В современных системах, к которым предъявляют жесткие требования по массогабаритным показателям, при определении пространственной ориентации в качестве сенсоров используются измеритель проекции угловой скорости на ось чувствительности (далее такие сенсоры будем называть гироскопами), измерители проекции ускорения на ось чувствительности (акселерометры) и измеритель проекции вектора магнитного поля (магнитный компас). В общем случае при определении пространственной ориентации в качестве основного источника информации используют интегрированные показания от трех датчиков угловой скорости, расположенных взаимно-перпендикулярно. С помощью информации, получаемой от акселерометра и магнитного компаса, оси чувствительности которых расположены так же, как и оси гироскопа, сводят к минимуму возникающую в процессе интегрирования угловой скорости ошибку, которая есть разница между реальной пространственной ориентацией и пространственной ориентацией, вычисленной с помощью датчиков угловой скорости[1]. Существует несколько кинематических параметров для описания движения твердого тела около неподвижной точки [2]:

Информатика, вычислительная техника и управление

• •    Углы Эйлера-Крылова;

• •    Матрица направляющих косинусов;

• •    параметры Родрига-Гамильтона (в компонентах кватерниона).

• •    параметры Кейли - Клейнав.

Применение кватернионов позволяет создать удобный и наглядный формализм, использующий параметры Родрига-Гамильтона для описания пространственной ориентации твердого тела, что является наиболее близким к оптимальному с точки зрения вычислительной техники [2, 3]. При описании пространственной ориентации удобно выделять три базиса:

• •    Опорный базис I, неподвижный в инерциальном пространстве, представленный в виде единичного кватерниона на рис. 1;

• •    Приборный базис Г — оцененная с помощью датчиков пространственная ориентация объекта;

• •    Связанный базис Е — базис, связанный с объектом ориентации.

  

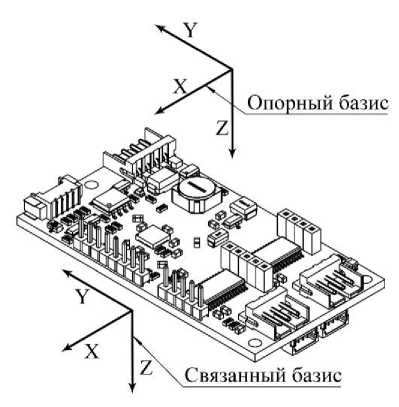
  Рис. 1. Расположение систем координат в связанном и опорном базисах

  
  
  
  

Fig. 1. Location of coordinate systems in local and world frames

Кватернионом называется упорядоченная четверка действительных чисел:

А=(Л о ,  Л 1 , Л₂, Л з ),                                           (1)

где Л₀ — скалярная часть; Л 1 ,Л₂, Л₃ — векторная часть.

Единичный кватернион представлен в виде:

Л=(1,  0,  0,  0).                                          (2)

Кватернион, описывающий пространственную ориентацию твердого тела, есть кватернион, описывающий поворот относительно единичного кватерниона. Из-за несовершенства датчиков угловой скорости, конечной разрядности чисел при представлении на ЭВМ с течением времени накапливается ошибка, которую можно выразить как разницу между опорным базисом и приборным. Для приведения приборного базиса к опорному (Г ^ I) коррекция должна осуществляться через изменение кватерниона поворота ДЛ, который находится путем интегрирования измеренной датчиком угловой скорости. При таком методе коррекции время приведения приборного базиса к опорному прямо пропорциональна ошибке между этими базисами. В момент включения системы ориентации необходимо за минимальный промежуток времени свести ошибку между опорным и приборным базисами к минимуму (произвести «выставку» системы ориентации). В работе [4] автор на время «выставки» предлагает увеличить коэффициент коррекции через который осуществляется приведение приборного базиса к опорному. Под коэффициентом коррекции понимается число , на которое умножаются компоненты коррекции перед изменением кватерниона поворота ДЛ. С учетом увеличения коэффициента коррекции «выставка» занимает время от 100 до 3000 итераций в зависимости от значения коэффициента коррекции и начальной пространственной ориентации системы (под итерацией понимается период интегрирования показаний гироскопа). Авторами предлагается алгоритм, позволяющий уменьшить ошибку оцененной пространственной ориентации до минимальной величины, которая определяется точностью акселерометров, за 10 итераций вне зависимости от начального положения системы.

Коррекция оценки ориентации приборного базиса . В монографии [3] авторы предлагают построение модели коррекции в векторной форме с помощью плоскости приведения, ориентиром для построения которой является вектор силы тяжести. Для построения полного приборного базиса нужны два неколлинеарных ориентира. В качестве второго ориентира может выступать вектор магнитного поля. В данной работе рассматривается исключительно коррекция на базе плоскости приведения.

Вектор при описании вращения кватернионами удобно выражать как кватернион, нулевая компонента которого (скалярная часть кватерниона) равна нулю

-_Е* = (0, Accel _x , Accel _y , Accel _z~ ) , (3) где - _Е * — вектор оценки линейных ускорений в связанном базисе, выраженный через кватернион; Accel _x — проекция оценки линейного ускорения на ось X акселерометра в связанном базисе; Accel _y — проекция оценки линейного ускорения на ось Y акселерометра в связанном базисе; Accel _z — проекция оценки линейного ускорения на ось Z акселерометра в связанном базисе.

Необходимо выполнить проекцию вектора оценки линейных ускорений из связанного базиса в опорный [4]:

-/=Л=- Е* оЛ, (4) где ц — вектор показаний акселерометра в опорном базисе, выраженный через кватернион; Л — кватернион текущей пространственной ориентации; Л — сопряженный кватернион текущей пространственной ориентации.

Умножение кватернионов не коммутативно, обозначается символом «=» и выражается системой уравнений (6-9) [5]:

N = Л = М,(5)

No = Л0М0 - Л^ - Л2М2 - Л3М3,(6)

N = Л0М1 + Л1М0 + Л2М3 - Л3М2,(7)

N = Л0М2 + Л2М0 + ЛзМ1 - Л1Мз,(8)

N3 = Л0М3 + Л3М0 + Л1М2 - Л2М1.

Кватернионом, сопряженным данному кватерниону Л, является кватернион, обозначаемый Л [6]:

Л=(Ло,  -Л1,  -Х2,  -A3).(10)

У сопряженного кватерниона векторная часть взята с обратным знаком (данный кватернион необходим для осуществления проекций из одного базиса в другой).

Вектор ориентира в опорном базисе выразим через кватернион:

-i = (0,    0,     0,     1),(11)

где - , — вектор ориентира в опорном базисе в выбранной системе координат, выраженный через кватернион (рис. 1).

В данном случае в качестве неподвижного ориентира выступает вектор силы тяжести в опорном базисе, так как выбор данного ориентира позволяет скомпенсировать ошибку ориентации по крену и тангажу. Компоненты вектора ориентира выбираются из следующих соображений:

• •    нулевой компонент равен нулю;

• •   1-й компонент — показание акселерометра по оси X при совмещении осей датчика с опорным

базисом;

• •   2-й компонент — показание акселерометра по оси Y при совмещении осей датчика с опорным

базисом;

• •   3-й компонент — показание акселерометра по оси Z при совмещении осей датчика с опорным

базисом.

Разница между вектором ориентира в опорном базисе и вектором оценки линейных ускорений в опорном базисе составит величину

• 8 ,    = - I - - I*                                                       (12)

Компоненты коррекции оценки пространственной ориентации в опорном базисе находим через формулу:

Информатика, вычислительная техника и управление

to ; — 5 / ° i-l ,

где to? — кватернион, содержащий компоненты коррекции кватерниона пространственной ориентации в опорном базисе.

Проекция компонент коррекции из опорного в связанный базис выражается через формулу toy — Л ° to? ° Л,

где toE — кватернион, содержащий компоненты коррекции кватерниона пространственной ориентации в связанном базисе.

С помощью to y корректируется оценка угловой скорости:

ДА = (1, sin

Ох^-( “' to* _E1) )-bt

, sin

⁽g> Y ^-(a- to* _E2 ⁾⁾-bt

, sin

(M Z -C^' Ш ез ))-Д£.

1),

где to_x — проекция угловой скорости на ось X гироскопа в связанном базисе; to y — проекция угловой скорости на ось Y гироскопа в связанном базисе; to_z — проекция угловой скорости на ось Z гироскопа в связанном базисе; Д( — период интегрирования показаний гироскопа; а — коэффициент пропорциональной коррекции, а > 0; ДЛ — кватернион поворота.

Коэффициент а выбирается из следующих соображений. При большом значении коэффициента возникает колебательный процесс компонент кватерниона, при малом значении коррекция не будет компенсировать ошибку, вызванную разного рода погрешностями при измерении угловой скорости, поэтому данный коэффициент выбирается из компромисса скорости приведения приборного базиса к связанному и отсутствия колебательного процесса.

Авторы в [2] вводят понятие кватерниона малого поворота. Если период опроса датчика очень мал, система физически не успеет повернуться на большой угол за отведенное время. С учетом этого целесообразно отказаться от функции вычисления синуса угла (тем самым уменьшив процессорное время расчета), т. к.

функция синуса вблизи нуля почти линейна. В кватерниона поворота:

этом случае

осуществляется линейная аппроксимация

ДЛ = (1,

⁽» Х ^-(“' > Е1 ))^-Д1

⁽to Y ^-(ct' " Ез ))'^

,

,

Oz-(“' > Ез⁾⁾ ' ^Д1;'

:).

Затем выполняется операция умножения кватернион малого поворота:

кватерниона текущей пространственной ориентации на

A t — A t-1 ° ДЛ,

где At — кватернион оценки пространственной ориентации; At-1 — кватернион оценки пространственной ориентации в предыдущий момент времени.

С учетом медленного ухода нормы кватерниона от единицы при реализации вычислений на ЭВМ, необходимо периодически производить нормирование кватерниона пространственной ориентации по формулам (19, 20), т. е. приводить норму кватерниона к единице:

II А ||— v2 + v2 + v2 + V2 ~ 1,(18)

где II А || — норма кватерниона;

|A| — T^+^+^+Tf,(19)

где |A| — тензор кватерниона;

_Vo_ У1 У2_ Уз

ANorm |W|,|W|,|W|,|W|, где AWorm — нормированный кватернион или верзор [1, 6].

Описанный выше алгоритм (3–20) осуществляет устойчивую коррекцию кватерниона пространственной ориентации через изменение оценки угловой скорости так же, как это происходит в алгоритмах Махони [8,10] и Маджвика [4]. Разница алгоритмов заключается в методике определения компонентов коррекции.

Алгоритм быстрой начальной инициализации кватерниона пространственной ориентации. Целью предлагаемого алгоритма является уменьшение времени приведения приборного базиса к связанному, причем коррекция осуществляется итерационно, посредством умножения кватерниона пространственной ориентации на кватернион коррекции.

Последовательность действий в алгоритме следующая:

• 1)    Опрос трех осей акселерометра;

• 2)    Определение компонент коррекции оценки ориентации по формулам (3–14);

• 3)    Преобразование компонент коррекции в кватернион поворота:

ДЛ = (1, sin — , sin — , sin—),                               (21)

2           2           2

где wj — первая компонента коррекции в связанном базисе; м2 — вторая компонента коррекции в связанном базисе; m J — третья компонента коррекции в связанном базисе.

• 4)    Кватернион текущей пространственной ориентации умножается на сопряженный кватернион поворота:

^ = ^ -1 о ДЛ.                                        (22)

• 5)  Выполняется нормирование кватерниона пространственной ориентации (19, 20);

• 6)    Возврат к шагу 1.

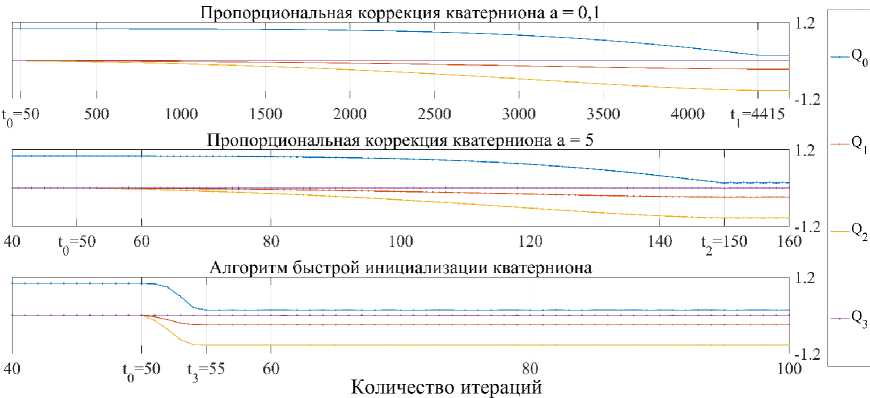
Эксперимент по определению времени переходных процессов компонент кватерниона при использовании разработаннгого алгоритма. Цель эксперимента — сравнить время переходных процессов компонент кватерниона при использовании коррекции через изменение оценки угловой скорости и коррекции по предложенному алгоритму. Описанные в данной статье алгоритмы приведения приборного базиса к связанному были реализованы на микроконтроллере dsPIC 33 EP 256 MU 806. В качестве датчика для определения пространственной ориентации использовался MPU 6050 — 3-х осевой гироскоп, измеряющий проекции угловых скоростей на свои оси чувствительности, и 3-х осевой акселерометр. Микроконтроллером вычислялись компоненты трех кватернионов пространственной ориентации по показаниям датчика при однократном измерении. Компоненты первого кватерниона вычислялись через изменение оценки угловой скорости с коэффициентом а = 0,1 (предварительный эксперимент со многими измерениями показал, что именно это значение является компромиссом между колебательным процессом и скоростью коррекции приборного базиса в течении всего времени работы данной системы ориентации). Компоненты второго кватерниона вычислялись через изменение оценки угловой скорости с увеличенным коэффициентом а = 5. Компоненты третьего кватерниона вычислялись по предложенному алгоритму быстрой инициализации. В момент включения и на протяжении всего эксперимента, датчик находился повернутым относительно горизонта по тангажу на 18 градусов и по крену на 174 градуса.

Number of itera tions is designated

Рис. 2. Переходные процессы компонент кватерниона в параметрах Родрига-Гамильтона.

Fig. 2. Transition processes of quaternion components in Rodrigues-Hamilton parameters

До момента времени t₀ = 50 микроконтроллер отправляет 3 единичных кватерниона для обработки в программу, работающую в интерпретируемой среде Matlab . В момент времени t₀ включается коррекция. В первом случае приведение приборного базиса к связанному завершается в момент времени t 1 = 4415. Во втором случае — в момент t₂ = 150. В третьем случае — в момент t₃ = 55. Признаком окончания коррекции является завершение переходного процесса компонент кватерниона:

Информатика, вычислительная техника и управление

A£_Qua£1=ti-to = 4365,

A£_Qua£2=t2 — to = 100,

^£_Qua£3   t3 — to   5, где ^£_QUa£ — количество итераций, за которое система ориентации скорректировала оценку пространственной ориентации в компонентах кватерниона в каждом из трех случаев.

Выводы. Предложенный алгоритм начальной выставки системы оказался быстрей в 873 раза по сравнению с коррекцией через оценку угловой скорости с коэффициентом коррекции a = 0,1 и в 20 раз быстрей по сравнению с коррекцией через оценку угловой скорости с увеличенным коэффициентом коррекции a = 5. В силу того, что кватернион поворота в данном алгоритме вычисляется только по показаниям акселерометров, то ошибка выставки системы будет прямо пропорциональна паразитному ускорению, действующему на систему. Под паразитным следует понимать любое ускорение, отличное от ускорения свободного падения. Поэтому после завершения начальной «выставки» необходимо отключать предложенный алгоритм и включать коррекцию через изменение оценки угловой скорости, как это предлагается в работах [4, 8].