Алгоритм нахождения всех простых чисел

В работе производится уточнение классификации чисел натурального ряда, доказательство теоремы о полном множестве простых чисел и детальное описание алгоритма нахождения всех простых чисел.

Согласно основной теореме арифметики [1], впервые точно сформулированной и доказанной в книге К.Ф. Гаусса в 1801 году, каждое натуральное число n > 1 единственным образом представимо в виде: к n =П РТ, (1)

1 = 1

где p 1 <  p ₂ < ... <  р_к - простые числа, а а 1 , ... , а _к -некоторые натуральные числа. Представление числа n в виде (1) называется его каноническим разложением.

Несмотря на особую роль соотношения (1) в теории чисел, его практическое применение, например для решения задач информационной безопасности, подчас затруднительно из-за вычислительной сложности оперирования с мультипликативным представлением натуральных чисел.

Вместе с тем, аддитивное представление любого составного числа через простые числа дает, с одной стороны, возможность существенного ускорения вычислительных процедур (в частности, при решении задач факторизации чисел), а с другой - позволяет эффективно подойти к решению многих математических проблем, включая проблему формального и однозначного описания полного множества простых чисел.

Аддитивное представление составных чисел вида {6к ± 1}, к = 1, 2, 3, ... впервые использовано в 2005 году при реализации программы «Линейный генератор простых чисел подряд», на которое получено свидетельство о регистра- ции [3]. В 2008 году опубликована работа, в которой приводится математическое описание формирования множеств как составных, так и простых чисел [4].

Уточнение классификации чисел натурального ряда

Для доказательства теоремы о полном множестве простых чисел уточним классификацию чисел натурального ряда.

С учетом того, что в современной математике натуральные числа определены неоднозначно (на самом деле, например 2 - одновременно простое и четное, 9 - одновременно нечетное и составное, 5 - одновременно нечетное и простое), для удобства дальнейшего изложения уточним их классификацию.

Для этого весь ряд натуральных чисел разобьем на следующие последовательные циклы подмножеств:

{ п_кД } = 6 к + l ,                 (2)

где к = 0, 1, 2, 3, .„; l = 1, 2, 3, 4, 5, 6.

Очевидно, что при к = 0

{ n 0,1 } = {1, 2, 3, 4, 5, 6}, далее при к = 1

{ n 1, i } = {7, 8, 9,10, 11, 12}, при к = 2

{ n_2l } = {13, 14, 15, 16, 17, 18} и т.д.

Таким образом, бесконечное множество чисел натурального ряда N состоит из сложения подмножеств {nkl}, где к = 0,1, 2, 3,...; l = 1, 2, 3, 4, 5, 6.       ’ l = 6 ГО

{ N } = UU { n M}.           (3)

l = 1 к = 0

Среди l простыми числами являются 2, 3 и 5, а 4 и 6 - составными. В каждом из подмножеств { n_kl } находятся и простые числа, и составные.

Определим l , при котором число в подмножестве { n_kl } может быть простым.

Очевидно, что при любом к и l , равном 2,4, 6, формируется подмножество четных (двукратных) чисел натурального ряда:

{C 2 } = {2, 4, 6, 8, ...}, члены которого образуются по формуле:

c m = 2 + 2 m ,                (4)

где m = 0, 1, 2, 3, 4 ... .

Напомним, что четных чисел в натуральном ряду - половина (50%), и их определение в данной работе - классическое.

Таким образом, первый член арифметической прогрессии (4) и ее разность равны первому простому числу 2.

Далее, для любого к при l , равном 3, формируется подмножество троекратных чисел натурального ряда:

{ C 3 } = {3, 9, 15, ...}, члены которого образуются с помощью соотношения:

c m = 3 + 6 m ,               (5)

где m = 0, 1, 2, 3, 4 ... .

То есть троекратные числа образуются арифметической прогрессией с первым членом, равным простому числу 3, и разностью, равной шести. Таких чисел в составе натурального ряда -одна шестая - 16,666...%.

Очевидно, что троекратные числа входят в подмножество нечетных чисел в их классическом определении (2 n + 1), n = 0, 1, 2, 3, 4. При этом четные числа, кратные шести, согласно нашему определению (5), не являются троекратными, а относятся к четным.

Итак, по определению - подмножества четных и троекратных чисел не содержат простых чисел, кроме 2 и 3 - первых членов арифметических прогрессий (4) и (5).

Осталось рассмотреть варианты l = 1,5.

С учетом того, что 6 к + 5 = 6( к + 1) - 1, очевидно, что подмножества:

{ ^- S } = {6( к + 1) - 1}, к = 0, 1, 2, 3, 4, ...

{ ⁺ S } = {6 к + 1}, к = 1, 2, 3, 4, ...       ⁽⁶⁾

содержат все простые числа, кроме 2 и 3.

В работах [4, 5, 8] числа 2 и 3 названы фундаментальными простыми числами . И для такого определения есть все основания. Именно эти два числа напрямую в (4) и (5) либо с использованием их произведения в (6) с добавлением, либо вычитанием единицы формируют все до одного числа натурального ряда, начиная с 2.

Соотношения (6), содержа все простые числа, кроме 2 и 3, также включают и составные числа вида { 6 n ± 1 } , n = 1, 2, 3, ... .

Для многих математиков, занимавшихся теорией чисел, задача - отделить друг от друга с помощью каких-либо формул, формальных процедур простые числа от составных, находящихся в множествах:

{ - S } = {6 n - 1}               (7)

{+S} = {6n +1}, n = 1, 2, 3, 4, ... , выступала на протяжении веков в качестве приоритетной задачи.

В таблице 1 для наглядности приведена бесконечная матрица последовательных циклов подмножеств { n_k , _l } = 6 к + 1 ; к = 0, 1, 2, 3, ...; l = 1, 2, 3, 4, 5, 6. В столбцах 1 и 5 жирным цветом выделены простые числа, большие или равные 5. В столбцах 2 и 3 в нулевой строке выделены фундаментальные простые числа 2 и 3.

Анализ таблицы 1 показывает, что в первом столбце, начиная со второй строки, располагаются простые и составные числа с избыточной единицей для деления нацело на шесть. Назовем их, в соответствии с работой [5], где впервые дано их определение, плюс простые числа (ППЧ) и плюс составные числа (ПСЧ).

Таблица 1

Последовательные циклы подмножеств

^{ nk , l ^} = ^{6 к + 1}

к / 1	1	2	3	4	5	6
0	1	2	3	4	5	6
1	7	8	9	10	11	12
2	13	14	15	16	17	18
3	19	20	21	22	23	24
4	25	26	27	28	29	30
5	31	32	33	34	35	36
6	37	38	39	40	41	42
7	43	44	45	46	47	48
n	6 n + 1	6 n + 2	6 n + 4	6 n + 5	6 n + 5	6 n + 6

В пятом столбце, начиная с первой строки, расположены простые и составные числа с недостающей единицей для деления нацело на шесть. Их, соответственно, определим как минус простые числа (МПЧ) и минус составные числа (МСЧ) [5].

Нетрудно видеть, что последовательность чисел в первом столбце, начиная с 7, описывается арифметической прогрессией:

• 7,7    + 6,7 + 2 • 6,...,7 + ( n - 1 ) - 6; n = 1, 2, 3, ... , (8) где первый член прогрессии равен 7, а ее разность - 6.

Поскольку первый член и разность прогрессии - натуральные взаимно простые числа, то она содержит, согласно теореме Дирихле о простых числах в арифметической прогрессии [6], бесконечное количество простых.

Аналогично последовательность чисел в пятом столбце, начиная с первой строки, описывается арифметической прогрессией:

• 5,5    + 6,5 + 2 - 6,...,5 + ( n - 1 ) - 6;n = 1, 2, 3, , ⁽⁹⁾ где первый член прогрессии равен 7, а ее разность - 6. Очевидно, что и эта прогрессия в соответствии с теоремой Дирихле содержит бесконечное количество простых, так как первый член - 5 и разность прогрессии 6 - натуральные взаимно простые числа.

Таким образом, арифметические прогрессии (8) и (9) формируют все до одного простые числа, кроме фундаментальных простых - 2 и 3.

Исходя из приведенных рассуждений, множество простых чисел есть объединение:

• •    двухэлементного множества { 2; 3 } ;

• •    вычитания из множества { ⁺ S } = { 6 к + 1 } ; к = 1, 2, 3, ... подмножества ПСЧ;

• •    вычитания из множества { - S } = { 6 к - 1 } ; к = 1, 2, 3, ... подмножества МСЧ.

Итогом выступает необходимая для дальнейших рассуждений классификация чисел натурального ряда на семь групп: четные числа; трехкратные числа; фундаментальные простые числа; минус простые числа; плюс простые числа; минус составные числа; плюс составные числа. Единица при этом выступает своеобразным «геномом» натурального ряда чисел.

Для нахождения полного множества простых чисел вида { 6 к ± 1 } , к = 1, 2, 3, ... формально опишем механизм образования ПСЧ и МСЧ.

Чтобы более наглядно представить этот механизм, а затем доказать теорему о полном множестве простых чисел вида { 6 к ± 1 } , к = 1, 2, 3, ... и реализовать алгоритм нахождения полного множества простых чисел (за исключением фундаментальных), расположим числа во множествах { ^- S } и { ⁺ S } друг против друга последовательно, начиная с 5 и 7 (таблица 2, жирным цветом выделены простые числа).

В таблице 2 введены следующие обозначения:

p i , i = 1, 2, 3, ... - простое число из множества { 6 к - 1 } ; к = 1, 2, 3, ... с недостающей единицей для деления нацело на 6 (МПЧ);

p i , i = 1, 2, 3, ... - простое число из множества { 6 к + 1 } ; к = 1, 2, 3, ... с избыточной единицей для деления нацело на 6 (ППЧ).

Таблица 2

Последовательности чисел из множеств { ^- S } и { ⁺ S }

Индекс числа, i	p - ; c -	p i ; c +
1	5	7
2	11	13
3	17	19
4	23	25
5	29	31
6	35	37
7	41	43
8	47	49
9	53	55
10	59	61
11	65	67
n	6 n - 1	6 n + 1

Соответственно, ci- составное число из множества { 6 к - 1 } ; к = 1, 2, 3, ... с недостающей единицей для деления нацело на 6 (МСЧ), а с + - составное число из множества { 6 к + 1 } ; к = 1, 2, 3, ... с избыточной единицей для деления нацело на 6 (ПСЧ).

Покажем, что все МСЧ и ПСЧ (таблица 2) образуются с помощью арифметических прогрессий, где основную роль играют только простые числа и число 6 - как произведение фундаментальных простых чисел. А именно, первые члены арифметических прогрессий образуются в виде произведений простых чисел самих на себя или на простое, стоящее напротив в таблице 2. Разность же в таких прогрессиях равна произведению простого числа на 6.

Но, прежде всего, рассмотрим, к какому типу (МСЧ и ПСЧ), в зависимости от типа простых чисел (МПЧ и ППЧ), относится их произведение.

Первый случай :

p i - p i = ( 6 i - 1 ) - ( 6 i - 1 ) = 36 i ² - 12 i + 1 =

= 6 i ( 6 i - 2 ) + 1 = 6 к + 1;           (10)

i = 1, 2, 3,     , где к = 2i(3i -1).

То есть результат произведения - плюс составное число (ПСЧ).

Второй случай :

pi- p+=( 6 i + 1)-( 6 i + 1) =

36 i ² + 12 i + 1 = 6 к + 1;            (11)

i = 1, 2, 3, ... , где к = 2i(3i +1).

И в этом случае результат произведения -ПСЧ.

Третий случай :

pi. p + =^{( 6} i - 1 ) . ( ⁶ i ⁺ 1 ) =

= 36 i ² - 1 = 6 k - 1;             ⁽¹²⁾

i = 1, 2, 3, … , где k = 6i2.

В данном случае – результат произведения простых чисел – минус составное число (МСЧ).

Нетрудно показать, что при несовпадении индексов сомножителей в произведениях (10) – (12) результаты будут такими же, а также легко проверить, что произведение простого числа на составное из множеств { 6 k ± 1 } ; k = 1, 2, 3, ... , а также произведение составных из тех же множеств подчиняется указанному правилу.

Из рассмотрения представленных случаев вытекает правило знаков – результат произведения любого количества простых чисел представляет собой ПСЧ, если в операции умножения участвует четное количество МПЧ, и МСЧ – в случае нечетного количества МПЧ.

А теперь рассмотрим алгоритм нахождения всех простых чисел подряд.

Алгоритм нахождения всех простых чисел

Первый шаг

Минимальное составное число (ПСЧ) в таблице 2 равно 25. Оно формируется в результате умножения МПЧ 5 на само себя. Далее прибавлением к 25 6 ∙ 5 = 30 формируется ПСЧ 55, затем к 55 прибавляется 30, получаем 85 и т.д. Таким образом, членами бесконечной арифметиче- ской прогрессии

25,25 + 5 • 6,25 + 5 • 6 • 2,25 + + 5 • 6 • 3,...,25 + 5 • 6 • n ,...,

где n = 0, 1, 2, 3, ..., выступает множество ПСЧ, первый член которого равен 5 ∙ 5 = 25, а разность равна 5 ∙ 6 = 30.

Важно отметить, что для получения всего множества ПСЧ как результата последовательного умножения 5 на нижестоящие числа второго столбца – 11, 17, 23 и т.д. нет никакой необходимости производить саму операцию умножения. Это связано с тем, что из-за цикличности чисел первого столбца в таблице 2, обусловленной последовательным получением следую- щего числа путем сложения предыдущего с числом 6, все соответствующие ПСЧ образуются во втором столбце как члены арифметической прогрессии (13).

Итак, необходимость перемножения первого простого числа 5 на все остальные числа во втором столбце заменяется аддитивной арифмети- ческой прогрессией:

I C ⁺ ) = ^ C ⁺ U 5 • 5 + 5 • 6 • n ;

⁵              p ₁

n = 0, 1, 2, 3, ... .

Второй шаг

Вычитаем из третьего столбца все ПСЧ, образованные арифметической прогрессией (14), и производим переиндексацию чисел, оставшихся в третьем столбце (таблица 3).

Третий шаг

Аналогично первому шагу находим следующее минимальное составное число. Оно равно произведению 5 ∙ 7 = 35 и является по определению минус составным числом (МСЧ). Следующее МСЧ для простого числа 5 можно было бы найти путем умножения 5 ∙ 13 = 65, затем следующее 5 ∙ 19 = 95, но мы не будем этого делать, помня о свойстве аддитивной арифметической прогрессии:

(C "1 = ( C ^- U 5 • 7 + 5 • 6 • n ;

⁵             p ₁

n = 0, 1, 2, 3, ... .

Таблица 3

Последовательности чисел из множеств { ^- S } и { ⁺ S } после первой переиндексации

Индекс числа, i	p " ; c i	+. + p i ; c i
1	5	7
2	11	13
3	17	19
4	23	31
5	29	37
6	35	43
7	41	49
8	47	61
9	53	67
10	59	73
11	65	79
n	6 n – 1	6 n + 1

Четвертый шаг

Вычитаем из второго столбца все МСЧ, образованные арифметической прогрессией (15), и производим вторую переиндексацию чисел (таблица 4).

Пятый шаг

Следующее минимальное составное число

(МСЧ) 7 ∙ 5 совпадает с 5 ∙ 7. Однако, выступая первым членом прогрессии, формирует ее с дру- гой разностью 7 ∙ 6 = 42:

{ C " } = ( C ^-J = 7 • 5 + 7 • 6 • n ;

i 7 >  I P 1 J

n = 0, 1, 2, 3, ... .

Таблица 4

Последовательности чисел из множеств { - S } и {⁺ S } после второй переиндексации

Индекс числа, i	p — ; c i	p + ; c i
1	5	7
2	11	13
3	17	19
4	23	31
5	29	37
6	41	43
7	47	49
8	53	61
9	59	67
10	71	73
11	77	79
12	83	91
13	89	97
n	6 n - 1	6 n + 1

Учет эффекта «пересечения» различных арифметических прогрессий, формирующих составные числа из множеств {6 n ± 1}, n = 1, 2, 3, ... , играет важную роль при решении задач интервальной оценки распределения простых чисел. Описание этого эффекта дано в работе [9, 10].

Шестой шаг

Вычитаем из второго столбца все МСЧ, образованные арифметической прогрессией (16), и производим третью переиндексацию чисел (таблица 5).

Таблица 5

Последовательности чисел из множеств { - S } и { ⁺ S } после третьей переиндексации

Индекс числа, i	— .    — Pi ; c	pt ; c i
1	5	7
2	11	13
3	17	19
4	23	31
5	29	37
6	41	43
7	47	49
8	53	61
9	59	67
10	71	73
11	83	79
12	89	91
n	6 n - 1	6 n + 1

Седьмой шаг

Наконец, для первой строки и третьего столб- ца простых чисел находим следующее составное число (ПСЧ), равное 7 • 7 = 49 и соответствующую арифметическую прогрессию:

= С + = 7 • 7 + 7 • 6 • n ; n = 0, 1, 2, 3, ... .

Восьмой шаг

Вычитаем из третьего столбца ПСЧ, образованные арифметической прогрессией (17), и производим четвертую переиндексацию чисел (таблица 6).

Важно отметить, что описанное последовательное нахождение составных чисел (МСЧ и ПСЧ) начинается с минимального ПСЧ, равного 25, а затем их «размножение» с помощью арифметических прогрессий, формирующих { c p _}, < С - ], < С ⁺ ] и ] С + ], дает возможность нахож-I Pi ) I Pi ! I Pi ) дения всех составных чисел подряд вида {6 к ± 1}; к = 1, 2, 3, ... без каких-либо пропусков. Также без пропусков находятся все простые числа вида {6 к ± 1}; к = 1, 2, 3, ... .

Таблица 6 Последовательности чисел из множеств

{ ^— S } и { ⁺ S } после четвертой переиндексации

Индекс числа, i	—   — p; c i	p + ; c +
1	5	7
2	11	13
3	17	19
4	23	31
5	29	37
6	41	43
7	47	61
8	53	67
9	59	73
10	71	79
11	83	97
12	89	103
n	6 n - 1	6 n + 1

Итак, в результате восьми шагов в таблице 6 до индекса i = 12 остались только простые числа. Повторяя последовательно восьмишаговую процедуру «фильтрации» простых чисел для других строк таблицы 6 путем удаления из множеств { ^— S } и { ⁺ S } составных чисел (МСЧ и ПСЧ), образуемых соответствующими арифметическими прогрессиями, можно найти все до одного простые числа в любом интервале от 1 до n . При этом однозначно определяется индекс любого ППЧ и МПЧ в указанном интервале.

Столь детальное описание алгоритма нахождения простых чисел сделано и для того, чтобы показать, что он в корне отличается от известных алгоритмов - решета Эратосфена и его модификаций (решета Сундарма и т.п.), а также решета Аткина и других современных алгоритмов.

В отличие от предыдущих, в данном алгоритме используются уравнения, описывающие механизм формирования составных чисел вида {6 к ± 1}, к = 1, 2, 3, ... и дающие возможность однозначно выделить все простые числа из множеств {6 к ± 1}, к = 1, 2, 3, ... [4, 8].

Покажем, что с помощью приведенного алгоритма находится полное множество простых чисел, за исключением фундаментальных простых чисел. Для этого докажем специальную теорему

Теорема о полном множестве простых чисел вида { 6 к ± 1 } , к = 1, 2, 3, ... .

Полное множество простых чисел вида { 6 к + 1 } , к = 1, 2, 3, ... формируется путем вычитания из множества {⁺ S } подмножества чисел, определяемых с помощью уравнений:

cp-- = P- • P- + P- •6 m cp+ = pp • pp + pp • 6m;          (18)

Pi i i it m = 0, 1, 2, 3, ... ; i = 1, 2, 3, ... , а полное множество простых чисел вида {6к -1}, к = 1, 2, 3, ... - путем вычитания из множества {-S} подмножества чисел, вычисляемых из соотношений:

c -- = Pi • Pt + Pi •6 m pi c-+ = pp • p- + pp • 6m;           (19)

Pi i I i I i m = 0, 1, 2, 3,    ; i = 1, 2, 3,    .

Для доказательства рассмотрим таблицу 2, в которой числа из множеств { ^- S } и { ^p S } расположены друг против друга с периодом 6 в виде двух бесконечных столбцов, начиная с минимальных - 5 и 7. Обозначим числа в указанных множествах, соответственно, как q ~ и q^p , i = 1, 2, 3, ... .

Очевидно, применительно к обозначениям в виде множеств, имеем:

{ q i } = { p? } и { c- } ;

{ q+H р-} и { c - 4          (20)

Минимальное составное число вида {6 к p 1}; к = 1, 2, 3, ... (т.е. минимальное ПСЧ) равно произведению минимального простого числа q - = 5 само на себя, т.е. q - - q - = c q . q = 25. Перемножая q - последовательно на все нижестоящие числа (таблица 2) во множестве { ^- S } , получаем последовательно без пропусков бесконечный ряд ПСЧ в виде:

{C-<}={q- • q-; q- • q -; q- • q 3;-.; q- • ql;-.}; (21) q1 ql при l ^ да.

Так как множество {-S} включает все простые и составные числа вида {6к -1}, i = 1, 2, 3, ... , очевидно, что путем последова- тельных умножений, отраженных в (21), в итоге получаем все до одного ПСЧ (см. правило зна- ков), куда входит в качестве сомножителя q1- .

Вычитая из множества { ^p S } подмножество { C - qq - } , при l > да , получаем бесконечное подмножество ⁺ S :

I q 1)

^p S { ' S } \ C:     , при l ^да ,    (22)

q1 J i ) I q • qi ;       1                  ’ состоящее из всех ППЧ и ПСЧ, за исключени- ем тех, куда в качестве сомножителя входит q1- .

На следующем шаге доказательства сформируем подмножество ^p S :

( q 2 )

pS - г = ) S - r \) Cp (, при /—>да,(23)

q 2 J            q1 J        q2 • qi ) р               ’ где

{Cp? q-} = { q - • q -; q -• q 3";...; q -• ql;..};

при l ^ да .

Очевидно, что подмножество { S q ^-} также состоит из бесконечного количества ППЧ и ПСЧ, куда в виде сомножителей не входят q ₁ ^- и q ₂ ^- .

Продолжая до бесконечности операции вычитания типа (22) и (23), получим подмножество:

f^p S - U{^p S } \f⁺ C - 3\f c p 3\...\f c ⁺- - }..., (25) ( q да; q да) I J ) q 1 • q l J ) q 2 • q l ,             ) qk■ q l J

(где l ^ да , к ^ да ), состоящее из всех ППЧ и ПСЧ, за исключением тех, куда в виде сомножителей входят числа из подмножества { ^- S } .

В общем случае:

{^p S - } = {^p s. - } \ { q i^- q - ; q^q^.;q ^- q - ^;4^{; (26)}

( Чк )      ( Чк -1 7

l ^ да.

Как нетрудно заметить, члены бесконечных подмножеств ПСЧ {C⁺_ - } в соотношениях (21), (24), (25) находятся иЗ уравнений арифметических прогрессий:

c - - = q - • q ," + q - • 6 m ; m = 0,1, 2,3. (27) q _i

Таким образом, мультипликативные соотношения в (21), (24), (26) замещаются на аддитивные в (27).

Нужно также указать, что при использовании в (27) не только простых pi-, i = 1, 2, 3, ... , но и составных, формируемых от простых, образуются «дубли» ПСЧ, однако это никак не сказывается на итоговом соотношении (25), предполагающем исключение на каждом шаге всех состав- ных, включая «дубли», образуемых соответствующими qk, к = 1, 2, 3, ... .

Чтобы получить полное множество всех плюс простых чисел (ППЧ), необходимо далее из множества (25) - {+ S„—} исключить все ПСЧ, q ГО образуемые числами из бесконечного множества {+ S} вида {6к +1}; к = 1, 2, 3, .... Минимальное составное число вида {6к +1}; к = 1, 2, 3, ..., образуемое числами из множества {+ S} вида {6к +1}; к = 1, 2, 3, ... равно минимальному простому q1 = 7, умноженному само на себя, q1 " q1 = cq+.qt = 49-

Перемножая q+ последовательно на все нижестоящие числа (см. таблицу 2) из множества {+ S}, так же как и в (21), последовательно, без пропусков получим бесконечный ряд ПСЧ в виде:

{ C + + »+ } = { q⁺ ■ ^{q +} ; ^{q +} ■ q ⁺ ; q + ■ q 3 ⁺ ;•••; q + ■ q l ;••• } ; ⁽²⁸⁾

\ q1 ql ) X                                                                           / при l ^ ro.

Поскольку множество { ⁺ S } включает по определению все простые и составные числа вида{6 к + 1}; к = 1, 2, 3, ... , получаем в (28) множество всех до одного ПСЧ, куда в виде сомножителя входит q + .

Вычитая из множества

подмноже-

/               X                                                  х q ro / ство {C ++ +}, при l ^ ro, получим бесконечное подмноясесТво ( + S —}, состоящее из всех ППЧ и ПСЧ, за исключением тех, куда в виде сомножителей входят все числа из {S} и q+ :

(⁺ S _ Д = Р S Д ( с + Д, при l ^ro. (29) I q ,; q 1 ) I q «J I q ■ qi ) ^{r                          v} '

Продолжая далее логику доказательства, реализованную в (21) - (26) применительно к системе последовательных вычитаний из множества { ⁺ S } подмножеств { C q^q _}; к = 1, 2, 3, ... ; l = 1, 2, 3, ..., в конечном итоге получим:

(⁺ S _ Д = [{ ⁺ S l\{⁺ S _}\(⁺ S _}\...\(⁺ S _)... \

( q го ; q „ j   L'    ' I   Ml    q 2) I qt) _

{ ⁺ S + } \ { ⁺ S + } \...\ { ⁺ S + } ...;        (30)

(     91)    (     ^q 2 J            (     9r )

при к м ro .

Поскольку из множества р S } вычтены все до одного ПСЧ вида {6к +1}; к = 1, 2, 3, ... , то есть все числа, образованные всеми возможны- ми произведениями, очевидно, что

{ ⁺ S — } = { p + } ; i = 1, 2, 3, ... ,       ⁽³¹⁾

^q ГО ; ^q ГО ) V )

где в правой части { p i ⁺} ; i = 1, 2, 3, ... есть полное множество плюс простых чисел (ППЧ) вида {6 к + 1}; к = 1, 2, 3,    .

Нетрудно видеть, что ПСЧ, входящие в бесконечные подмножества J C+ I в соотношени-( qr ql j ях (28) - (29), находятся из уравнений арифметических прогрессий:

c + + = q l ■ q l + q i ■ 6 m ; m - 0,1,2,3,.... (32)

И также соответствующие «дубли» составных чисел (ПСЧ), появляющиеся из-за использования в (32) не только простых, но и составных чисел, очевидно, не влияют на конечный результат в виде (31).

По аналогии с процедурой доказательства полноты множества ППЧ { p f } ; i = 1, 2, 3, ... , использующей соотношения (21) - (32), для нахождения полного множества МПЧ { S q _ГО - q _ГО } = { p i } ; i = 1, 2, 3, ... сформируем минимальное составное число вида {6 к — 1}; к - 1, 2, 3, ... .

Очевидно, используя правило знаков, минимальное МСЧ равно произведению минимального простого числа q — = 5 на число, стоящее напротив в таблице 2, т.е. на q + = 7, при этом q ? q + = c - - . _q + = 35.

Перемножая q ₁ ^— последовательно на все нижестоящие числа (см. таблицу 2) из множества { S } , получаем последовательно без пропусков бесконечный ряд МСЧ в виде:

— — + — + — + — + о —о+ I = { q1 ■ q1 ; q1 ■ q2; q1 ■ q3 ;...; q1 ■ ql ;...}; (33) q1 ql J X / при l ^ ro.

Так как множество {+ S} включает все простые и составные числа вида {6к +1}, к - 1, 2, 3, . , то путем последовательных умножений, отраженных в (33), получаем все до одного МСЧ (см. правило знаков), куда в виде сомно- жителя входит q1 .

Вычитая из множества { S } подмножество { C ,^-_-^l } , при l ^ro , получаем бесконечное подмножество ^— S _— :

{ ^{— S}q r } = {^{— S} } \ { C q — — ^ г } , при ^l ^ ^ГО ,     ⁽³⁴⁾

состоящее из всех МПЧ и МСЧ, за исключени- ем тех, куда в качестве сомножителя входит q—.

Продолжая до бесконечности операции вычитания типа (34), получим подмножество:

(- S UР S }\( с" 3\( с ₊Ь-\( С" Л-, (35)

( q „"] I ) l^qrq/ +J l q2-- qi+)        V^itiiJ где l ^ro, к ^ro, состоящее из всех МПЧ и МСЧ, за исключением тех, куда в виде сомножителей входят числа из подмножества {— S}.

Члены бесконечных подмножеств ПСЧ { C _{— +} } в соотношениях (33) - (35) находятся из уравнений арифметических прогрессий (19):

c - = q, • q + + q, •6m; m - 0, 1,2,3,., (36) qi при этом мультипликативные соотношения замещаются на аддитивные.

Чтобы получить множество всех минус простых чисел (МПЧ), необходимо далее из множества (35) - { ^- S q - } исключить все МСЧ, образуемые числами из бесконечного множества { ' S } вида {6 к + 1}; к = 1, 2, 3, .

Минимальное МСЧ вида {6 к - 1}; к = 1, 2, 3, ... , образуемое числами из множества { ⁺ S } вида {6 к + 1}; к = 1, 2, 3, ... , равно, как и в предыдущем случае, q + • q - = c . _ q — = 35.

Перемножая , 1 последовательно на все нижестоящие числа (см. таблицу 2) из множества {^- S } , также без пропусков получим бесконечный ряд МСЧ в виде:

{ +    - . +    - . +    —

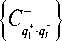
9 1 • 9 1 ^; 9 1 • 9 2 ^; 9 1 • 9 3

9 r 9 l ;...};     (37)

при l ^ да .

Так как { ⁺ S } включает по определению все простые и составные числа вида {6 к + 1};

к = 1, 2, 3, ... , получаем в (37) множество всех до одного МСЧ , куда входит 91+ .

Вычитая из множества {^- S - } подмножество { С - ₉ _ } , при l ^ - , получим бесконечное подмножество <^- S ₊ >, состоящее из всех МПЧ и

I 9 - ; 9 1 )

МСЧ, за исключением тех, куда в виде сомножителей входят все числа из { ^- S } и , + :

(^- S- _{+ +}М^- S - Д\( С - Л,    (38)

9-; 9 -; 91                 9-; 9 -            91 • 9i при l ^ -.

Продолжая далее последовательные вычитания из множества < ^- S ₊ >  подмножества ) С - L ⁹ - ^{; 9}                                          _:^

к = 2, 3, ... , I = 2, 3, ... в конечном итоге полу- чим:

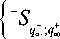
) = Г{^- s }\(^- s )\(^- s )\...\Р s 1.1 \ ) L^{1 1} t 9 1 J t 9 2 J          l 9к ) J

P S ₊1\( S ₊ |\...\f S ₊ L- , при к ^-. ⁽³⁹⁾ ( 9 1 ) ( 9 2 J ( 9к )

Очевидно, что

{ - ^S -J = { P - } , i = 1, 2, 3, .   (40)

⁹ - ; ⁹ - J      \ J

МСЧ, входящие в бесконечные подмножества { C ^. _9i - } в соотношениях (37) - (39), находятся из уравнений арифметических прогрессий:

c + = 9 + • 9= + 9 + • 6m, m = 0, 1, 2, 3, ... , (41) qi ii i и в этом случае «дубли» МСЧ, появляющиеся из-за использования в (41) не только простых, но и составных чисел, не влияют на конечный результат в виде (40).

Таким образом, теорема о полном множестве простых чисел вида { 6 к ± 1 } , к = 1, 2, 3, ... доказана.

Используя результаты доказательства теоремы, восьмишаговый циклический алгоритм на- хождения всех простых чисел подряд, который мы описали, можно существенно упростить, используя формальное представление механизма образования составных чисел вида {6к ± 1}, к = 1, 2, 3, ... в виде (18) - (19).

Основными особенностями предлагаемого ниже алгоритма являются:

• •    простота реализации по сравнению с другими алгоритмами нахождения простых чисел;

• •    линейная зависимость времени расчета от числа n натурального ряда;

• •    возможность быстрого вычисления всех простых чисел подряд из множеств {6 к ± 1}, к = 1, 2, 3,    .

Суть алгоритма заключается в реализации следующих пяти этапов.

• 1.    Определяется натуральное число n , применительно к которому необходимо вычислить все простые числа, его не превосходящие.

• 2.    Вычисляются два ряда проиндексированных натуральных чисел q i и q + , i = 1, 2, 3, ... из множеств {6 к - 1} и {6 к + 1}, к = 1, 2, 3, ... , не превосходящих n .

• 3.    Находятся все решения следующих уравнений, не превышающие n .

• 4.    Из множества {6 к - 1}, к = 1, 2, 3, .„ вычитается объединение множеств { с ,^-- } U { С - + } , i = 1, 2, 3, .„ , а из множества {6 к + 1}, к = 1, 2, 3, .„ - объединение множеств { С , ;} ^ { C_q ⁺ ₊ } , i = = 1,2,3, _ .                         "       "

• 5.    Полученные в результате операций вычи-

• тания простые числа, не превышающие n, располагаются в порядке возрастания, и каждому простому присваивается соответствующий индекс j = 1, 2, 3, _ .

^ = 97- 979 97-6 m cq+ = q,+ - qiq qt-6 m c- = 97- qi9 97-6m cit = 97- 97 9 97-6m,           (42)

qi m = 0, 1, 2, 3, _ ; i = 1, 2, 3, _ .

Отметим, что использование 9_i вместо p_i в соотношениях (42) значительно:

• •    ускоряет (и упрощает) процедуру нахождения простых чисел из-за отсутствия операций промежуточного вычитания и переиндексации чисел, использованных в описанном восьмиша-

• говом циклическом алгоритме;

• •    упрощает различные оценочные операции работы алгоритма в связи с тем, что разница между стоящими друг против друга q i и , 7 всегда равна 2.

При этом итоговые результаты работы по нахождению всех простых чисел вида {6 к ± 1}, к =

= 1, 2, 3, … в интервале (0, n ) остаются теми же, что и при применении детализированного восьмишагового алгоритма.

Безусловно, возникают дополнительные вычисления, связанные с нахождени-

При n >> 1

q

n

i 9 ( m 2 e

•h 2 1 • '-----2

2 n

-

3 (

^{m 2 E} q ,

) . (47)

ем вторичных, третичных и т.д. «пересечений», формирующихся в уравнениях (24). Например, все ПСЧ, формируемые арифметической прогрессией { С 5 } = 5 • 5 + 5 • 6 • m ; m = = 0, 1, 2, … , включают все ПСЧ от арифметических прогрессий { С 255 } = 25 • 25 + 25 • 6 • m ; { С + ₂₅ } = 625 • 625 + 625 • 6 • m ; m = 0, 1, 2, и т.д.

Однако преимущества использования уравнений (42) вместо (18) и (19) при вычислении

Для q образуется только одно плюс составное число, равное:

Г = q 2 . max       max

Оно находится из уравнения (47) при m = 0:

q max

1 'E- ¹

2 n

простых чисел в смысле скорости и простоты

расчетов существенно превышает те издержки, которые возникают в связи с необходимостью

учета дополнительных вторичных, третичных и т.д. «пересечений».

В таблице 7 приведен пример работы алгоритма нахождения простых чисел до 1000.

Индекс плюс и минус простых чисел указан курсивом в центральном столбце таблицы. Правый от центрального столбец содержит ППЧ (выделены жирным шрифтом) и ПСЧ. Левый от центрального столбец содержит МПЧ (выделены жирным шрифтом) и МСЧ. Все остальные столбцы справа содержат ПСЧ вида {6 к + 1}, k = 1, 2, 3, … , образуемые первыми двумя уравнениями (42) и не превышающие 1000.

Соответственно, остальные столбцы слева содержат МСЧ вида {6 к - 1}, к = 1, 2, 3, ... , образуемые последними двумя уравнениями (42) и не превышающие 1000. Нижние индексы составных чисел равны первым членам арифметических прогрессий (42).

Оценим зависимость qi  от n. Для начала рассмотрим первые два уравmнax ения (42).

Очевидна справедливость следующего ра-

венства:

q ² + 6 q , • m + 6 q , • E q - n = 0;

i = 1, 2, 3, … ; m = 0, 1, 2, 3, … ,

где q , = q , ^- или q , в зависимости от выбора уравнения; E _q - коэффициент, отражающий разность между n и последним членом арифметиче-

ских прогрессий, описываемых первыми двумя уравнениями (42).

По определению:

⁰ <  ^E <  1.               (44)

Уравнение (43) имеет единственный положительный корень:

q , = ^{- 3} ( m ² E q ) ² 9( ( m ^{2 E} q ) ² n ,     ⁽⁴⁵⁾

или

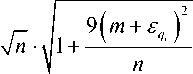
^{- 3} ( ^{m 2 E} ) .

При больших n

q ~v- max

Из (50) и (44) следует:

Учитывая

отсюда

q max

max

n -

max

= 6I max

q max

- * 3 Eq-	(49)
3 E q .	(50)
< v n .	(51)
± 1,	(52)
+ 1 .	(53)

Применительно к рассмотренному примеру n = 1000:

т.е.

28,6 <  q <  31,6, max

q, = 31;     = 5, max          max что соответствует правой части таблицы 7 для ПСЧ.

Для левой части, оценивая q , - , можно использовать и третье, и четвертое у^mр^axавнения (42).

Из третьего уравнения (42) следует

q , ( q , 2 2 ) 2 6 q , • m 2 6 q , • e

qi

= 1, 2, 3, … ; m = 0, 1, 2, 3, … . Отсюда

- n = 0;

q

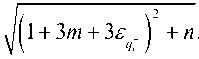
По аналогии с предыдущим рассмотрением, применительно к МСЧ

q,  =- 12 3e - max                  q

n

( 1 2 3 E ) 2

1 2 ³----- q ^, (56)

n

также при n >>  1:

q - » V n - 1

max

Отсюда, используя (44),

Учитывая

имеем:

q

1, max

q,   = 6 i ax -1, max max

n max

.

Таблица 7

Минус составные числа до 1000										q i -	8 S	qi +	Плюс составные числа до 1000
- 31 • 29	- 29 • 31	- 25 • 23	- 23 • 25	- C 19 • 17	- 17 • 19	- C 13 • 11	- 11 • 13	C 7 -• 5	C 5 -• 7				+ 5 • 5	+ 7 • 7	+ 11 • 11	+ 13 • 13	+ 17 • 17	+ 19 • 19	+ 23 • 23	+ 25 • 25	+ 29 • 29	+ 31 • 31
899	899	575	575	323	323	143	143	35	35	5	1	7	25	49	121	169	289	361	529	625	841	961
		725	713	437	425	221	209	77	65	11	2	13	55	91	187	247	391	475	667	775
		875	851	551	527	299	275	119	95	17	3	19	85	133	253	325	493	589	805	925
			989	665	629	377	341	161	125	23	4	25	115	175	319	403	595	703	943
				779	731	455	407	203	155	29	5	31	145	217	385	481	697	817
				893	833	533	473	245	185	35	6	37	175	259	451	559	799	931
					935	611	539	287	215	41	7	43	205	301	517	637	901
						689	605	329	245	47	8	49	235	343	583	715
						767	671	371	275	53	9	55	265	385	649	793
						845	737	413	305	59	10	61	295	427	715	871
						923	803	455	335	65	11	67	325	469	781	949
							869	497	365	71	12	73	355	511	847
							935	539	395	77	13	79	385	553	913
								581	425	83	14	85	415	595
								623	455	89	15	91	445	637
								665	485	95	16	97	475	679
								707	515	101	17	103	505	721
								749	545	107	18	109	535	763
								791	575	113	19	115	565	805
								833	605	119	20	121	595	847
								875	635	125	21	127	625	889
								917	665	131	22	133	655	931
								959	695	137	23	139	685	973
									725	143	24	145	715
									755	149	25	151	745
									785	155	26	157	775
									815	161	27	163	805
									845	167	28	169	835
									875	173	29	175	865
									905	179	30	181	895
									935	185	31	187	925
									965	191	32	193	955
									995	197	33	199	985
										203	34	205
										209	35	211
										215	36	217
										221	37	223
										227	38	229
										233	39	235
										239	40	241
										971	162	973
										977	163	979
										983	164	985
										989	165	991
										995	166	997

Пример работы алгоритма нахождения простых чисел до 1000

Для нашего примера n = 1000:

31,6-4 < q- < 31,6 -1, imax т.е.

q- = 29, a q = 31, i_max = 5. i max                  i max             max

И это соответствует левой части таблицы 7 для МСЧ.

Обобщая полученные результаты зависимости q_i от n , имеем следующую простую оценку - "M x аксимальное число q + вида { 6 k + 1 } , k = 1, 2, 3, … , участвующее в алгоритме формирования составных чисел (МСЧ и ПСЧ), равно целой части n :

C*[ A ]'(60)

Соответственно, q,- = Г Tn I- 2.(61)

max

При этом индекс imax равен i "ax =[ ^ ] .(62)

В заключение отметим, что доказательство теоремы о полном множестве простых чисел вида {6 k ± 1}, k = 1, 2, 3, ... и формальное описание механизма формирования составных чисел в виде аддитивных прогрессий [4, 8] дало возможность предложить и реализовать простой и эффективный алгоритм нахождения всех простых чисел подряд, что выступает фундаментальным достижением в области математики. Представляется, что дальнейшее использование нового математического аппарата, описывающего формирование простых и составных чисел вида {6 k ± 1}, k = 1, 2, 3, ... , приведет в ближайшей перспективе к серьезным изменениям и открытиям в теории чисел и прикладных областях, связанных с применением простых чисел.