Алгоритм наведения управляемой ракеты класса «воздух-воздух» с активной радиолокационной головкой самонаведения на вертолет при различном характере его полета

Цитирование: Богданов, А.В. Алгоритм наведения управляемой ракеты класса «воздух-воздух» с активной радиолокационной головкой самонаведения на вертолет при различном характере его полета / А.В. Богданов, С.А. Горбунов, А.А. Кучин, А.А. Хадур // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(7). С. 829–842. DOI: 10.17516/1999-494X-0269

можением, полет в режиме «висение» [7-9]. Кроме того, методы и алгоритмы синтезированы без учета результатов экспериментальных исследований информационных свойств сигналов, отраженных от вертолета.

В работе под методом наведения понимаем закон формирования требуемой фазовой траектории, наведение по которой позволит поразить цель, а под алгоритмом - правило формирования управляющих сигналов, именуемых также параметрами рассогласования, по которому определяется несоответствие реальных фазовых координат x _yi объекта управления (ОУ) их требуемым значениям x _Ti (i=1,r) [10-12].

Цель статьи – на основе СТОУ в пространстве состояний синтезировать оптимальные по минимуму локального функционала качества метод и алгоритм наведения авиационной УР с АРГС на вертолет при различном характере его полета с учетом результатов летно-экспериментальных исследований (ЛЭИ) информационных свойств РЛ-сигналов, отраженных от реального вертолета.

Экспериментальные исходные данные

В результате ЛЭИ информационных свойств РЛ-сигналов, отраженных от вертолета [7, 8, 13], сущность которых заключается в регистрации с помощью специальной аппаратуры, установленной в состав бортовой радиолокационной станции (РЛС) истребителя МиГ-31 сигналов, отраженных от реального вертолета при различном характере его полета, и их обработка в лабораторных условиях на основе использования узкополосного спектрального анализа, позволили сделать следующие выводы.

Во-первых, РЛ-сигнал, отраженный от вертолета, спектральный доплеровский портрет которого представлен на рис. 1, имеет сложную структуру, обусловленную отражениями сигнала от: фюзеляжа вертолета; вращающихся лопастей несущего винта, имеющих различную радиальную скорость; вращающихся частей силовой установки вертолета [7, 8, 14].

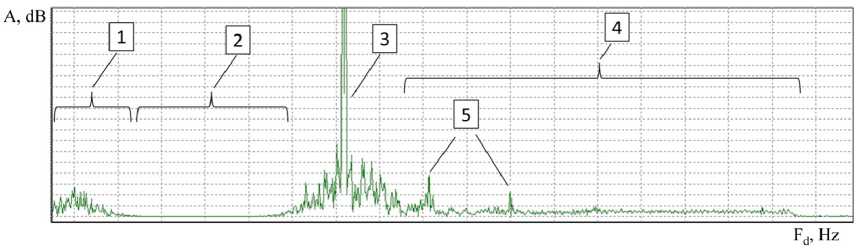
Рис. 1. Спектральный доплеровский портрет сигнала, отраженного от вертолета: 1 – отражения от подстилающей поверхности; 2 – зона режекции фильтра в бортовой РЛС истребителя (куда устанавливалась аппаратура регистрации); 3 – отражения от фюзеляжа вертолета; 4 – отражения от вращающихся лопастей несущего винта вертолета; 5 – отражения от вращающихся частей силовой установки вертолета

Fig. 1. Spectral Doppler portrait of the signal reflected from the helicopter: 1 – reflections from the underlying surface; 2 – rejection area; 3 – reflections from the helicopter fuselage; 4 – reflections from the rotor blades of the helicopter; 5 – reflections from the power plant of the helicopter

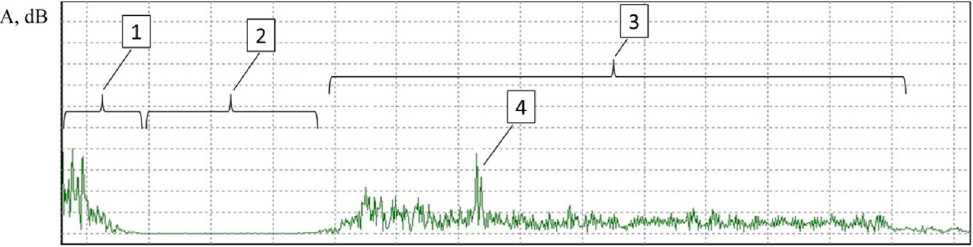
Fd, Hz

Рис. 2. Спектральный доплеровский портрет сигнала, отраженного от вертолета со скоростью менее 60 м/с: 1 – подстилающая поверхность; 2 – зона режекции; 3 – отражения от вращающихся лопастей несущего винта вертолета; 4 – отражения от вращающихся частей силовой установки вертолета

Fig. 2. Spectral Doppler portrait of the signal reflected from the helicopter at a speed of less than 60 m/s: 1 - reflections from the underlying surface; 2 – rejection area; 3 – reflections from the rotor blades of the helicopter; 4 – reflections from the power plant of the helicopter

Во-вторых, при полете вертолета со скоростью менее 216 км/ч (60 м/с) (в том числе и при полете в режиме «висение») отражения от фюзеляжа вертолета попадают в зону режекции, в этом случае будут наблюдаться (рис. 2) только отражения от вращающихся лопастей несущего винта вертолета и от вращающихся частей силовой установки вертолета.

Кроме того, известно [7, 8], что отражения РЛ-сигнала от вращающихся частей силовых установок летательных аппаратов имеют явную ракурсную зависимость. Поэтому для данной ситуации в качестве оценки скорости V_c6 сближения в режиме «висение» целесообразно использование значений доплеровских частот спектральных составляющих РЛ-сигнала, отраженного от вращающихся лопастей несущего винта вертолета [7, 8].

Таким образом, на основе анализа результатов ЛЭИ информационных свойств РЛ-сигналов, отраженных от вертолета, можно заключить, что как при стационарном полете (со значительной скоростью), так и при ускорении (торможении) вертолета целесообразным является использование при синтезе метода и алгоритма наведения УР с АРГС доплеровских частот, обусловленных скоростью сближения УР с фюзеляжем вертолета, а при полете в режиме «висение» - доплеровские частоты, обусловленные скоростями сближения УР с вращающимися лопастями несущего винта вертолета.

Постановка задачи на синтез

В общем случае задача синтеза метода и алгоритма наведения ракеты на воздушную цель в рамках СТОУ в пространстве состояний формулируется следующим образом [10, 11]: для системы с заданной частью

х(0 = Fy (r)xy (0 + Ву (Г)и(О + ^. (О,                                    (1)

предназначенной для отработки процесса x,(» = F,(Ox,(O+4,(O -                                        (2)

при наличии измерений

z(O = H(Ox(O + t(O найти закон управления

u(O = K XQ^CO-iyCO]

оптимальный по минимуму локального функционала качества

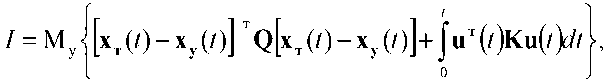
где F _y ( t ) - динамическая матрица состояния процесса х_у (t );

x _y (t) - n-мерный вектор управляемых фазовых координат;

В _у ( t ) - матрица эффективности управления;

u ( t ) - r-мерный вектор сигналов управления (r

^ _y ( t ) - n-мерный вектор центрированных гауссовских возмущений процесса х_у(Г)с известной матрицей G _y односторонних спектральных плотностей;

F _T ( t ) - динамическая матрица состояния процесса х_т (/);

x _T ( t ) - n-мерный вектор требуемых фазовых координат;

^ _т ( t ) - n-мерный вектор центрированных гауссовских возмущений процесса х_т (0 с известной матрицей G _т односторонних спектральных плотностей;

H(t) – матрица связи обобщенного вектора состояния           с m-мерным вектором наблюдений (измерений) (m≤n);

^( t ) - n-мерный вектор центрированных гауссовских шумов измерений с известной матрицей G и односторонних спектральных плотностей;

К – матрица штрафов за величину сигналов управления;

– матрица, определяющая способность системы воспринимать сигналы управления;

Q – матрица штрафов за точность управления           ;

М у – математическое ожидание при условии, что имеются результаты измерения хотя бы части фазовых координат х _у и х т .

Принятые допущения при синтезе метода и алгоритма

• 1.    Каналы управления ракетой в горизонтальной и вертикальной плоскости независимы, в дальнейшем рассматривается только горизонтальная плоскость, результаты ее рассмотрения могут быть применимы и для вертикальной плоскости.

• 2.    При самонаведении на борту управляемой ракеты формируются значения требуемого поперечного ускорения.

• 3.    УР и вертолет могут маневрировать с поперечными к линии визирования «УР-вертолет» ускорениями j _p и j _ц соответственно, а ускоряться - с продольным к линии визирования «УР-вертолет» ускорением j прод ;

• 4.    Под различным характером полета вертолета понимается любое из возможных его состояний:

• - стационарный полет – горизонтальный полет вертолета в турбулентной атмосфере, при котором постоянные значения скорости V _B , высоты Н и курса не изменяются во времени;

• - ускорение (торможение) – полет вертолета, при котором постоянные значения скорости V _в , высоты Н и курса могут изменяться во времени;

• - режим «висение» – полет вертолета, при котором скорость V _в ≈ 0 м/с, а высота Н и курс

постоянны во времени.

Динамическая модель взаимного перемещения УР и вертолета при различном характере его полета

На рис. 3 представлена схема взаимного расположения УР и вертолета (вид сверху).

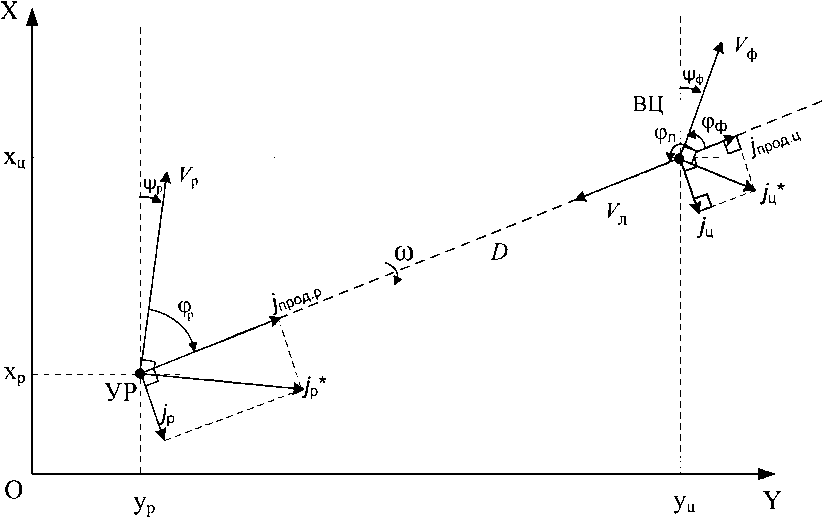
Рис. 3. Взаимное расположение УР и вертолета (вид сверху)

Fig. 3. The relative position of the rocket and the helicopter (top view)

На рис. 3 обозначено:

• D – расстояние между УР и фюзеляжем вертолета ВЦ класса «вертолет»;

• ω – угловая скорость вращения линии визирования между УР и вертолетом;

V р – текущая скорость УР;

• j прод.р – продольное к линии визирования ускорение УР;

• j р – поперечное к линии визирования ускорение УР;

• φ р – текущее значение бортового пеленга вертолета с УР;

• ψ р – текущее значение курса полета УР;

• V ф – скорость перемещения фюзеляжа вертолета;

• V л – линейная скорость вращения наступающей лопасти несущего винта вертолета;

• j прод.ц – продольное к линии визирования ускорение вертолета;

• j _ц – поперечное к линии визирования ускорение вертолета;

• φ ф – угол между линией визирования и линией пути фюзеляжа вертолета;

• φ _л – угол между линией визирования и вектором линейной скорости вращения наступающей лопасти несущего винта вертолета (≈180°);

(х _ц , у ц ) - координаты вертолета (цели);

(x р , у р ) – координаты УР.

Скорость V _ц полета вертолета можно представить в виде

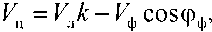
где k – коэффициент, компенсирующий «ошибочное» принятие скорости лопасти за скорость вертолета в целом, определяется по формуле

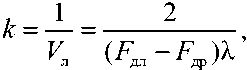
где F др - частота Доплера, обусловленная собственной скоростью управляемой ракеты;

F д_л - частота Доплера, обусловленная собственной линейной скоростью вращения наступающей лопасти несущего винта вертолета управляемой ракеты;

λ – длина волны.

Проецируя скорости V р и V ц на линию визирования и нормаль к ней, получаем

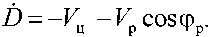
Подставляя (6) в (8), получаем

D® = К - ^ s^m Фф ^{+ р} ₽^sm Фр■                                     ⁽⁹⁾

Для упрощения примем допущение, что косинусы всех углов примерно равны единице, а синусы – своим аргументам.

Дифференцируя (9) по времени при V _р =const получаем

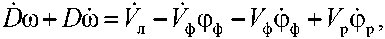
. ^л-^фФф Мф^+КрФр Dm

0) =-----

D      D D

или

Так как 1 _рф_р = j_p , К_фф_ф = ;_ф, а 1ф - Г_ф(р_ф = /_продц, выражение (11) можно записать в виде

q V р "Р 7 пред ц 7ф / q ®

В случае, когда К ф ~0 (режим «висение»),

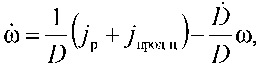
где 7продц    -Т

Для определения изменения бортового пеленга вертолета в процессе наведения на него вертолета представим формулу (9) как

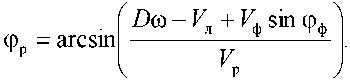
Дифференцируя (14) по времени при V _р =const, получаем

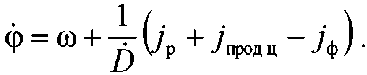
Таким образом, на основании формул (12) и (15) динамическая модель, описывающая взаимное перемещение УР и вертолета при различном характере его полета, имеет следующий вид:

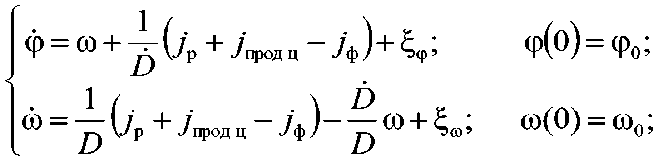
7>=-к„;

D(O) = Do;

Грц(0) = Грц0;

Упрод (°) = УпродО ’

К = /   ■ рц 7прод ’

Упрод — _Фпрод + ^упрод ’ где ^w , ^j - центрированные гауссовские шумы, характеризующие случайные возмущения системы «УР-вертолет»; α – коэффициент, характеризующий маневренные свойства УР.

Данная динамическая модель взаимного перемещения УР и вертолета будет в дальнейшем положена в основу синтеза оптимального метода и алгоритма наведения УР на вертолет.

Синтез метода и алгоритма наведения ракеты на вертолет

Для синтеза закона управления ракетой необходимо иметь модель состояния (1), (2) и функционал качества в виде (5).

Исходя из того, что параметр управления – поперечное ускорение УР, вектор управления будет иметь вид и=Л +Уцродц-Уф-                                        (18)

Требуемыми параметрами для управления ракетой, учитывающими управление ракурсом РЛ наблюдения в АРГС ракеты отраженных от вертолета РЛ-сигналов и угловой скоростью вращения линии визирования «УР-вертолет», являются ф_т и го_т соответственно, т.е. вектор требуемых фазовых координат х _т будет иметь вид

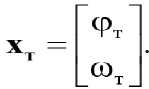
Управляемые параметры для системы самонаведения УР – φ и ω, т.е. вектор управляемых фазовых координат x у будет следующим:

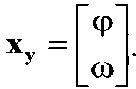
Так как параметром управления служит боковое ускорение ракеты j р, а управляемыми параметрами - ф и го, то матрицу эффективности сигналов управления В_у образуют коэффициенты при векторе управления u в динамической модели (16):

.

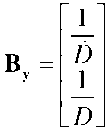
Матрицы штрафов за точность наведения Q и величину сигналов управления K в формуле (4) с учетом размерности матриц (19)–(21) имеют вид

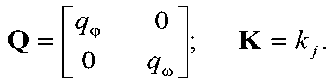
В результате функционал качества (5) принимает вид

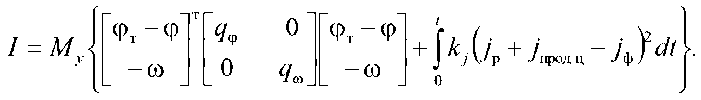
Подставив (18)–(22) в (4), получим следующее соотношение:

или

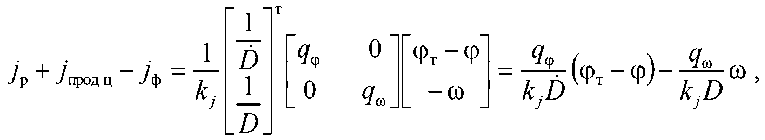
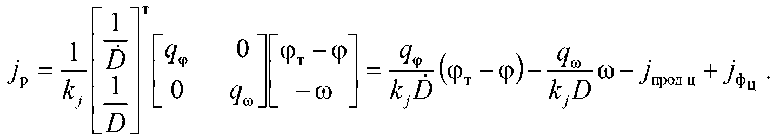
Выполнение при синтезе условий линейно-квадратично-гауссовской задачи [10, 11] по- зволяет заменить истинные значения фазовых координат векторов хт и ху их оптимальными оценками, тогда алгоритм траекторного управления имеет вид

^j j рт Л ’

7рт — Г (фт — ф)— 7 А ® — 7прод ц "*" 7ф kjD       kjD где Aj - параметр рассогласования, определяющий несоответствие текущего jр и требуемого jрт значений поперечного ускорения ракеты.

Учитывая, что , а выражение (27) в случае использования при наведении УР с АРГС доплеровских частот, обусловленных скоростью сближения УР с фюзеляжем вертолета, можно представить в виде

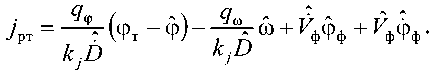
а при полете в режиме «висение», когда при наведении используются доплеровские частоты, обусловленные скоростями сближения УР с вращающимися лопастями несущего винта вертолета,

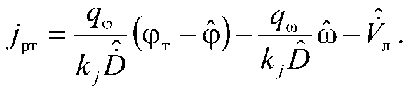
Для формирования сигналов управления в соответствии с алгоритмом (26) необходимо иметь оценки следующих координат:

• -    дальность D «ракета-вертолет» и скорость ее изменения;

• -    пеленг j вертолета с управляемой ракетой;

• -    угловая скорость w вращения линии визирования «УР-вертолет»;

• -    поперечное ускорение j ф фюзеляжа вертолета, либо продольное ускорение j _прод.ц вертолета.

Анализ полученных моделей состояния, а также сравнительный анализ полученных метода и алгоритма наведения с алгоритмами наведения, представленными в [3, 4, 10–12], позволяют сделать следующий вывод: применение нового алгоритма траекторного управления при наведении ракеты на вертолет при различном характере его полета позволит обеспечить непрерывное наведение управляемой ракеты класса «воздух-воздух» с АРГС, независимо от того, измерима ли скорость вертолета в целом (доплеровская частота сигнала, отраженного от фюзеляжа) или только от вращающихся лопастей несущего винта вертолета. С этой целью необходимо обеспечить бессрывное сопровождение вертолета в АРГС по доплеровской частоте.

Техническое решение для обеспечения бессрывного сопровождения вертолета

Для эффективного функционирования синтезированного алгоритма наведения ракеты класса «воздух-воздух» с АРГС, определяемого выражением (27), в [15] предложено следующее техническое решение бессрывного сопровождения вертолета в АРГС ракеты.

На рис. 4 приведена блок-схема, поясняющая данное техническое решение, на рис. 5 ( а-е) -эпюры, поясняющие его.

Бессрывное сопровождение вертолета в АРГС ракеты заключается в следующем [15] .

На вход блока 1 БПФ (рис. 4) на промежуточной частоте с выхода приемника АРГС поступает сигнал S ( t ) (рис. 5а), отраженный от вертолета, который подвергается узкополосной доплеровской фильтрации на основе процедуры БПФ и преобразуется в амплитудно-частотный спектр S ( f ) (рис. 5 b ), составляющие которого обусловлены отражениями сигнала от фюзеляжа А ф сопровождаемого вертолета и вращающихся лопастей его несущего винта A i .

С выхода блока 1 БПФ (рис. 4) на первые входы пороговых устройств 2 и 3 поступают соответственно значения амплитуд А ф и A_i амплитудно-частотного спектра S ( f ) отраженного от

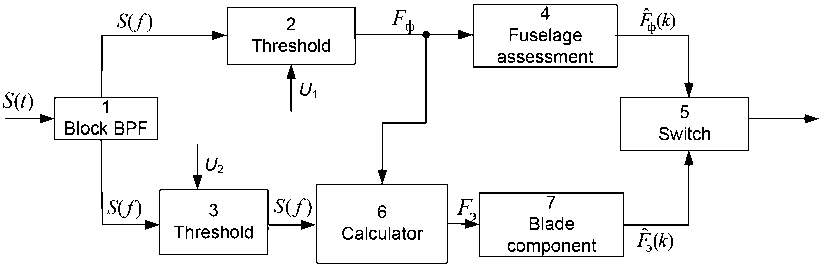
Рис. 4. Блок-схема

Fig. 4. Flowchart

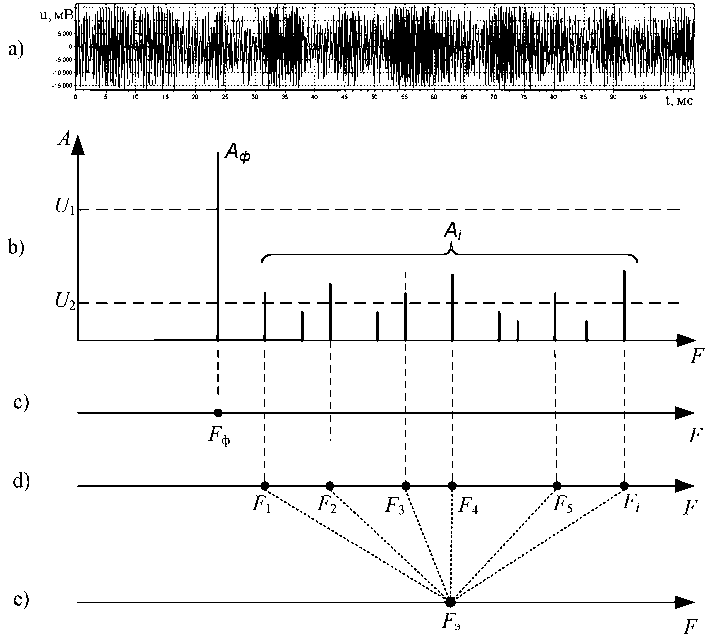
Рис. 5. Эпюры

Fig. 5. Diagrams вертолета сигнала. На их вторые входы подаются значения порогов U1 и U2. Причем значение порога U2 в n раз меньше значения порога U1.

В каждый k -й дискретный момент времени на выходе первого порогового устройства 2 определяется отсчет F ф доплеровской частоты (рис. 5 c ) спектральной составляющей с максимальной амплитудой А ф , превысившей первый порог U ₁ и соответствующей отражениям сигнала от фюзеляжа вертолета, который подается (рис. 4) на вход первого фильтра 4-го сопровождения. В результате на его выходе формируется оценка рф ( k ) доплеровской частоты, которая поступает на первый вход коммутатора 5.

Одновременно с определением отсчетов F ф доплеровских частот, соответствующих отражениям сигнала от фюзеляжа вертолета, в каждый k -й дискретный момент времени определяются отсчеты F i амплитуд А i , превысивших второй порог U 2 и соответствующих отражениям сигнала от лопастей несущего винта вертолета (рис. 5 d ), за исключением спектральной составляющей с максимальной амплитудой А ф и соответствующей отражениям сигнала от фюзеляжа вертолета.

В вычислителе 6 (рис. 4) в соответствии с выражением

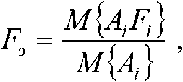
где М{…} – операция математического ожидания; Ai – i-я амплитуда спектральной составляющей сигнала, соответствующая отражениям сигнала от лопастей несущего винта вертолета, вычисляется один отсчет Fэ доплеровской частоты (рис. 5e), соответствующий энергетическо-– 839 – му центру отражений сигнала от лопастей несущего винта вертолета, который подается на вход второго фильтра 7 (рис. 4) сопровождения, где осуществляется фильтрация полученных отсчетов Fэ доплеровских частот, соответствующих энергетическому центру отражений сигнала от лопастей несущего винта вертолета, в результате чего на его выходе формируется оценка V (к) доплеровской частоты по отражениям сигнала от лопастей его несущего винта, которая поступает на второй вход коммутатора 5.

На выходе коммутатора 5 при наличии отсчетов F ф доплеровских частот спектральных составляющих, превысивших первый порог U 1 и соответствующих отражениям сигнала от фюзеляжа вертолета, формируется оценка F_h( к ) доплеровской частоты с выхода первого фильтра 4 сопровождения вертолета по отражениям сигнала от его фюзеляжа, а при наличии отсчетов F i доплеровских частот спектральных составляющих, превысивших второй порог U 2 и не превысивших первый порог U 1 - оценка / ,( к ) доплеровской частоты с выхода второго фильтра 7 сопровождения вертолета по отражениям сигнала от лопастей его несущего винта.

В результате обработки зарегистрированных реальных РЛ-сигналов, отраженных от различных типов отечественных вертолетов, установлено [7, 8, 13] следующее:

амплитуда спектральной составляющей сигнала, отраженного от фюзеляжа вертолета А ф , в 10-12 раз превышает амплитуды А _i спектральных составляющих сигнала, отраженного от лопастей несущего винта вертолета, то есть величина порога U ₂ должна быть меньше в 10-12 раз величины порога U 1 ;

диапазон доплеровских частот, занимаемый отражениями сигнала от лопастей несущего винта вертолета, составляет 8–12 кГц;

численное значение отсчета F _э доплеровской частоты (рис. 5 e), соответствующее энергетическому центру отражений сигнала от лопастей несущего винта вертолета, вычисляемого в соответствии с выражением (30), отличается на 12-15 % от значения отсчета доплеровской частоты, вычисленного в виде математического ожидания отсчетов доплеровских частот амплитуд А i , то есть точность оценки доплеровской частоты У (k) выше относительно точности оценки доплеровской частоты, получаемой на основе фильтрации отсчетов доплеровской частоты, соответствующих математическому ожиданию отсчетов доплеровских частот амплитуд А i .

Выводы

• 1.    На основе СТОУ в пространстве состояний синтезированы оптимальные по минимуму локального функционала качества метод и алгоритм наведения авиационной УР с АРГС на вертолет при различном характере его полета.

• 2.    Предложено техническое решение по бессрывному сопровождению вертолета при различном характере его полета с учетом результатов летно-экспериментальных исследований информационных свойств РЛ-сигналов, отраженных от него.