Алгоритм нулевого листа в задаче подавления интерференционных шумов на изображениях

В основе многих современных измерительных приборов, применяемых в промышленности, лежат алгоритмы обработки изображений. Ярким примером такого устройства может служить лазерный триангуляционный сканер, измеряющий профиль объекта. Основной вклад в погрешность данного устройства вносит интерференционный шум. Данный шум носит мультипликативный характер. Добиться его полной компенсации классическими методами фильтрации затруднительно [2], так как наличие этого шума определяется профилем измеряемой поверхности, а также ее шероховатостью. Для компенсации интерференционного шума предлагается использовать методы слепой обработки, не требующие априорной информации о фильтруемом сигнале. При этом получаемое изображение на матрице рассматривается как двумерный скалярный сигнал.

Возможности слепой идентификации скалярных двумерных сигналов несколько шире, чем одномерных, что исторически привело к более интенсивному внедрению методов слепой обработки в данном случае. Хорошо известно, например, что ковариационные функции стационарного процесса на выходе линейной системы не содержат информации о фазе ее передаточной функции и слепая идентификация сигнала по модулю передаточной функции возможна только для узкого класса систем с минимальной фазой. Для дискретных случайных полей это, вообще говоря, не так. Это означает, что для двумерных дискрет- ных сигналов возможности восстановления фазы по модулю передаточной функции значительно шире [4]. Объяснение этому факту заключается в том, что в кольце полиномов от двух и более переменных над полем комплексных чисел существует достаточно мощное множество неприводимых полиномов в отличие от кольца полиномов от одной переменной, где, как известно, не существует неприводимых полиномов, степень которых больше единицы. Поэтому если двумерный дискретный сигнал имеет z-преобразование, неразложимое на более простые множители, то, очевидно, используя единственность факторизации многочлена на неприводимые множители, мы можем восстановить дискретный сигнал по его автокорреляции, или, что эквивалентно, по его амплитудному спектру. Данное свойство двумерных сигналов можно использовать и для решения задачи детерминированной слепой идентификации канала формирования изображения. В качестве практического алгоритма подавления интерференционных шумов в данной работе предлагается использовать алгоритм нулевого листа [1].

Группировка корней полинома

Рассмотрим двумерный сигнал (изображение), полученный на входе системы

g(x,y) = f(x,y)*h(x,y) ,         (1)

здесь Лм) – исходный сигнал, Kx,y> – функции рассеяния точек (импульсная характеристика), сквозь которые прошел исходный сигнал f(x,y). Особенностью алгоритма нулевого листа является то, что он позволяет определять все функции рассеяния как неприводимые полиномы. Из теории преобразования Фурье известно, что

Ж y) * h_v (x, y) *... * h_k (x,y)^

F(tox,roy)Hv(tox,roy)...H2(tox,toy).

В случае дискретного сигнала, которым и является исходное изображение размером N × M пикселей, получаем дискретное преобразование Фурье в виде:

дг_] д/_|                .2лтк 27ml

G(k,l) = g(m,n)e ^{7 A/} e ^{7 w} . (3)

/1 = 0 /77=0

.1лк

Введя замену переменных и = е м и 2 яп v = e N , мы получаем полиномиальную форму представления изображения:

N-\ М-\

GYi,Y = ^^gYnaiVV .   (4)

77=0 /77=0

Проведя факторизацию полинома G и обратное дискретное преобразование Фурье, мы получаем исходное изображение №yY При этом следует отметить, что факторизация для данного полинома является однозначной и единственной, тем самым обеспечивая устойчивое решение [1]. Начальным этапом алгоритма нулевого листа является фиксация значения ll - Mq ) в результате чего полином G(w₀,v) становится одномерным:

G{u₀,v) = ^_ta_n(u₀)vⁿ,             (5)

/7=0

где коэффициент апИ определяется значением комплексного параметра м и g(m, n):

aA^^^glm^u™ •       (6)

Коэффициенты an можно найти в матричном виде, а именно:

So.o	go,l "	g(),N-l	( 1,0 ) u'
§М-2,0	gM-2,\ "	"  gM-2,N-2
g M-1.0	gM-\,0   "	" Sy-l.N-y	/V-l Vм 7

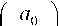
На следующим этапе находятся корни уравнения у^и\ i = \,2,-—,N -1 , полученного приравниванием полинома (5) к нулю при заданном параметре и = u₀:

5°7MoK = °-

/7 = 0

Поиск корней уравнения осуществляется с использованием компаньонной матрицы C(v) , определяемой как

	л 0	1 •	■■       0
C(v) =	0	0       •	1	■ (9)
	Др	ax	_ aN-2
	( aN-\	aN-\	aN-\ J

При этом поиск корней уравнения сводится к решению уравнения:

det(C-/,/) = 0, (10) где Zi является корнем уравнения (10), а также элементом собственного вектора у матрицы C . Перепишем выражение (4) в виде:

G(u,v) = F(u,v^H(u,v~), (11)

где F(u,v) – исходный сигнал, HVu,Y – функция размытия точек.

Введем в рассмотрение два множества S p и S p . Множеству S _F принадлежат все корни полинома F(u,vY а множеству S p все корни полинома H(u,v) при фиксированном и = zz₀ . После того как корни относительно переменной V разнесены по соответствующим множествам S_F и S_H , производится фиксация v = v₀ и задача решается уже относительно переменной и , при этом получаются корни u,(v), i = V,2...M — 1 с разнесением по множествам ^F ^ . Основной проблемой является то, каким образом соотнести корни уравнения к тому или иному множеству.

Рассмотрим пример группировки корней в случае фиксированного значения U =Uq. В качестве начального значения используем u₀ = 1,0. Для фиксированного значения v = v₀ подход аналогичен. На рис. 1 представлен пример начального распределения корней для полинома восьмой степени.

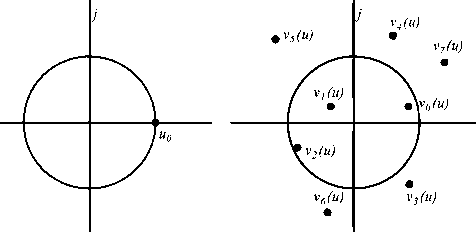
Рис. 1. Начальное распределение корней

Из полученных корней выбирается произвольная пара корней V,. И _Vj с таким условием, что i Ф j . При этом количество таких пар равно N(N-Y/2. Изменением комплексного параметра добиваемся сходимости корней, то есть Vj = Vj = v . При этом комплексный параметр U принимает значение и = u , а в комплексной точке U = U V = V выполняется условие

^G(z7,v) = 0.                (12)

ОУ

Распишем частную производную по переменной и выражения (11):

+ Н(и,v)—F(u,v),           (13)

Su если V,- g SF ; Vj eSH — G^u,v) = 0. Тем самым du '

данный критерий может быть использован для идентификации принадлежности корней полино-

Для сближения корней v/и v; необходимо d ,

— D <0. С учетом того, что в (21) все элементы ds являются комплексными, можно записать

ма тому или иному множеству.

Проблемой, решаемой на данном этапе, является задача сведения корней. Для ее реше-

/?oexp(>o) = (v*-vy>

G,Au,v,A

GAt^Vj)

GiMVil

Gv(u,vA

;(22)

ния произведем замену переменных, положив,

что и И V зависят от некого параметра S , то есть и = u(s) ^; V = v(s) . Найдем производную G[z/(s),v(s)] no 5 и приравняем ее к нулю – тем dv

dzz

exp(J0) • ds

Перепишем (19) с учетом (22) и (23):

самым определим зависимость , пользуем в дальнейшем:       ds

которую ис-

dD

SG[zz(s),v,(s)] dzz   SG[zz(s),v,(s)] dv, du ds dv      ds

—— = 2 Re р₀ ехр(7^₀)^ exp(j9) . (24) ds                     ds

ds

= 0,(14)

dG[z/(s),v₇(s)]dw ₊ 5G[zz(s),v_y(s)]dv_/ du ds dv ds

0.(15)

dD2

Из выражения (24) видно, что ---<0 при ds

Ф_о + 9 = к . Отсюда следует, что для сведения корней V,- И V_;- параметр и надо перемещать в направлении О = л -ф₀ на величину

Введем новые обозначения G,.—", dG                             ®^u

G_ = . ■ Из выражений (14)-(15) получим dv

Azz =

dzz ds

ехр(л" - ^>0)As

dv, _ G„ (zz,v,) dzz ds G,,(zz,v,) ds ’

где ^o определяется соотношением

dv,. _ С_м(и,У_гН и ds G_v(u,v ) ds

Сведение корней полинома сводится к уменьшению расстояния D между ними, которое определяется соотношением

S2 =|v,--V/|2 =(v/-v/)(v*-v*). (18)

Продифференцировав (18) по переменной ^ , находим

dD2

---= 2 Re

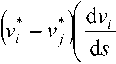
dv,

• (19)

С учетом выражений (16)-(17) получаем

dv,. dvy

ds ds

G^u^^ Gll(u,vi')

Gv(zz,v;) Gv(zz,v,)

^-(20) ds

Перепишем выражение (19) c учетом (20), получим:

d^² _{= 9} I «) ^GMvj) _ G>yvj ds       P '     ] Gjzz.v ) С>,у₅)

dzz

^r(2D ds

% = arg)

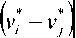
Gu(u,Vj)

G^u-VjA

GMAil

GvGi,vA

■(26)

Для определения модуля перемещения комплексной величины Azz разложим вызываемую этим перемещением величину v в ряд Тейлора, ограничившись второй степенью:

dv ,     1 d"v z v + Av = vH--Azz H(Azz)2. (27)

dzz       2 dzz dv d2v

Значения         определим, воспользовав- dzz dzz шись неявной теоремой:

dv ₌ G„(zz,v) dzz G_r(zz,v)

v„„            P---[g (zz,v)G2(z/,v)- dzz G,3(zz,v)L

-2G„v(zz,v)G„(zz,v)G1,(zz,v)+ Gw(zz,v)G2(zz,v)]. (29)

Разложение в ряд Тейлора позволяет вычислить корни V,- И Vj полинома лишь однажды, на этапе получения начального распределения корней, а корни, получаемые на последующих итерациях, определять при помощи ряда Тейлора. Использование ряда Тейлора позволяет при реа-

лизации алгоритма использовать распараллеливание при сведении корней, тем самым увеличивая быстродействие алгоритма в разы. Для того чтобы определить модуль All , введем коэффициент к , который задает соотношение между линейной составляющей Au и нелинейной (Az/)², откуда получаем неравенство:

T^L^l^— < k .   (3Q)

v„ A и

M 11         I max

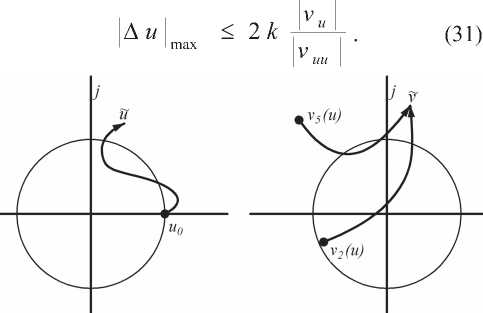
Рис. 2. Пример сведения корней

При сведении корней полной сходимости получить на практике не получается из-за наличия аддитивного шума – для устранения этой проблемы вводится минимальное расстояние между корнями ^mm ' если ^Vr^Vi корни считаются сближенными. После того как корни сближены, то есть V, = V j = v и и = и , необходимо произвести корректировку значенияи ИГ,воспользовавшись методом Ньютона решения системы уравнений

Г G(m,v) = O

1                ■                         (32)

K(?/,v) = o

После того как все корни сведены, строится матрица группировки корней «s, элементы которой определяются соотношением

S(i,j) = \G_u(u,v)\,           (33)

где kj определяют номер соответствующих корней в начальном распределении (рисунок 1). Ниже приведен пример матрицы для полинома восьмой степени:

" 1 0,12  0   0   0  Q34  0   0"

Q12 1   0   0   0  0,25  00

0   0   1  0,22  0   0  Q180

0   0  Q22  1   0   0  Q160

8=

0   0   0   0   1   0   0Q42'

Q34 Q25  0   0   0   1   00

0   0  Q18 Q16  0   0   10

0   0   0   0  Q42  0   0   1,

При наличии аддитивного шума нулевые элементы матрицы S могут отличатся от нуля. На практике данные значения составляют порядок 1O"⁵...1O"⁷, для фильтрации вводится порог ^nop порядка 10 ⁵ и проводится пороговая обработка матрицы S в соответствии с выражением:

SUJ^

i, s^»^; о, SUJ)< £_nop.

Проведя пороговую обработку, получаем:

"1   1  0  0  0  1  00"

1 10 0 0 100

0  0  1   1   0  0   10

_    0  0  1   1  0  0  10

5 =                              . (35)

0  0  0  0  1  0  01

1 10 0 0 100

0  0  1   1   0  0   10

чо  о  0  0  1  0  01

Из матрицы (35) видно, что имеется три группы корней:

(1  1  0  0  0  1  0  О) - группа I;

(0  0  1  1  0  0  1  О) - группа II;

(0  0  0  0  1  0 0  1) - группа III.

Данный пример показывает возможность работы алгоритма, в случае если исходный сигнал прошел через несколько искажающих систем с импульсными характеристиками H_x (u, v), Hi (u, v)... H _N (u, v) . Это свойство алгоритма выделяет его на фоне остальных алгоритмов, используемых в слепой обработке.

Формирование выходного изображения

После того как сформировались группы корней, необходимо сгенерировать факторы для интересующей нас группы корней [3]. В нашем случае имеется два фактора группы i : A^u, v) для случая множеств S p и S p и BjG^v) для случая множеств T_F и T_H . Вычисление этих факторов аналогично друг другу и в случае А₆(и,у) может быть записано в виде:

NR

^^’^"П^’-^^^]’ (36)

где               uk = ехр(-]2ттк / M), k = 0;l...M-\, vn = exp( - jinn / M); n = 0; 1... 2V — 1;

NR - число корней в группе z; v_m (и_к ) - корень т -ой группы I при и = и_к . Стоит отметить, что A^u^V) и B^u,v) по своей сути имеют размерность M^N и N^M соответственно. Интересующая нас матрицам,_; выходного изображения может быть найдена из системы матричных уравнений

Л,=сАм в = diai.j ■

Систему (37) перепишем в виде ад-С)вИ^.

В общем случае выражение (38) можно переписать в виде:

Ex = 0,                         (39)

С учетом того что размерность матрицы Г составляет (M + TV) X (MN), прямое решение уравнения (35) представляет определенные трудности. Для его решения воспользуемся соотношением:

Г^Гх = 2x,               (40)

где X – константа, а вектор x ищется как собственный вектор матрицы получаемый в результате опе-т рации ГТ.

% 0 0 4.1 •■•    0 ■■•    0 -в,. "By 0 0 ■■•     0 ■■•     0 0 0 ■■■ 4.j ~BM] 0 ■■•     0 4,2 0 •■•    0 0 "4.2 ■■•     0 F = 0 4.2 •■•    0 0 "4,2 ■■•     0 (41) 0 0 ’ ' ’ 4^.2 0 ~BM^ ...     0 A.n 0 •■•    0 0 0 - -4„v 0 4,.v •■•    0 0 0 ■■■ — b^n <0 0 ■■• A^ 0 0 ■ ' ’ 4м, Л у После того как собственный вектор найден и из него выделены интересующие нас элементы С] ... сдг и dy ... d, выходная матрица (выходное изображение ) Q. j ищется как произведение a^=A c”1;                (42)

или аи=ВчВ.              (43)

На рис. 3 представлено исходное изображение с триангуляционного сканера, полученное после сканирования цилиндрического вала.

Рис. 3. Исходное изображение

После обработки данного изображения алгоритмом нулевого листа было получено изображение, показанное на рис. 4: видно, что большую часть интерференционных шумов удалось подавить. Оставшиеся искажения на изображении можно объяснить малым динамическим диапазоном матрицы и эффектом блюминга, выражающимся растеканием заряда между чувствительными фотоэлементами при их насыщении.

Рис. 4. Изображение после обработки

Заключение

В статье представлено детальное описание алгоритма нулевого листа, из которого видно, что данный алгоритм представляет непростую вычислительную задачу. По этой причине алгоритм долгое время не находил практического применения. Однако в связи с появлением процессоров с возможностью обработки информации в несколько потоков данный алгоритм может получить внедрение. В отличие от большинства существующих алгоритмов, алгоритм нулевого листа имеет возможность получить из входного сигнала не только интересующий нас сигнал, но и искажающие его составляющие.