Алгоритм обнаружения дубликатов на цифровых изображениях с использованием эффективных линейных локальных признаков

В современном мире цифровые изображения являются одним из основных источников информации в различных сферах жизнедеятельности. Фотографии являются подтверждением каких-либо событий, космические снимки отражают состояние какой-либо территории и т.д. Изображения могут быть искажены злоумышленниками с целью скрыть или изменить информацию, содержащуюся в них.

Самым часто используемым способом подделывания изображения является копирование и вставка области этого же изображения. Такие атаки будем называть дублированием фрагментов цифрового изображения, а копируемые области – дубликатами. Существует большое количество работ [1–4], посвящённых разработке алгоритмов обнаружения подобных атак: общим в них является разработка некоторых признаков, инвариантных к различным искажениям дубликатов (яркостные, геометрические), вычисляемых для положений скользящих окон с перекрытиями. В работе авторов [5] рассматривался подход к обнаружению дубликатов без искажений, в основе которого лежало вычисление значений разработанных хэш-функций. В данной работе речь пойдёт о разработке новых хэш-функций, на основе которых будет построен алгоритма обнаружения неискажённых дубликатов.

Работа построена следующим образом. В первой части дано краткое определение дубликата и хэш-функции, а также координатного шаблона, лежащего в основе алгоритма обнаружения. Вторая часть посвящена собственно разработке алгоритма поиска дубликатов по координатному шаблону. В третьей части приводятся краткие теоретические сведения об эффективных линейных локальных признаках (ЛЛП). Четвёртый раздел посвящён разработке оптимальной хэш-функции на основе ЛЛП. В пятом разделе приводятся экспериментальные исследования предложенной хэш-функции и выявляются оптимальные параметры алгоритма обнаружения дубликатов по шаблону. В заключении приводятся выводы и даются рекомендации по использованию разработанных хэш-функции и алгоритма.

1.    Понятие дубликата и хэш-функции

По аналогии с работой [6], определим цифровое изображение размера MXN как отображение вида:

• f : N m х N n ^ B ⁸,

где B = { 0,1 } , N M - множество целых чисел

{ 0,1,-.., M - 1 } .

Определим также координатный шаблон как ко нечное множество координат {(0,0),...,(m,n)}, обла- дающее следующими свойствами:

– координатный шаблон содержит координату (0,0);

– координатный шаблон не содержит координат с отрицательными значениями;

– координатный шаблон является четырёхсвязным [6].

Введём также в рассмотрение специальный вид координатного шаблона, обозначаемый далее X ( 3 , a , b ) и задаваемый следующим образом:

X ( 3 , a , b ) = U П ( a , b , m , n ) , ( m , n ) e3

где множество координат П ( a , b , m , n ) задаётся в виде

( m, n ) , ( m, n + 1 ) ,..., ( m, n + b - 1 ) ,

П ( a , b , m , n )

( m + a - 1, n ) ,

, ( m + a - 1, n + b - 1 )

а конечное множество неотрицательных координат 3 может быть достаточно произвольным, но гарантирующим выполнение для X(3, a, b) свойств коорди- натного шаблона (совпадающие пары координат считаем одним элементом множества).

Будем говорить, что на изображении присутствуют дубликаты по шаблону X(3, a, b), если существует по крайней мере две пары координат (m', n‘) и (m", n"), для которых выполняется следующее множество равенств:

f (m'+ m, n'+ n ) = f (m "+ m, n " + n),

V ( m , n ) e X ( 3 , a , b ) .

Приведённая система равенств по сути означает поэлементное совпадение фрагментов изображения, расположенных в позициях (m', n') и (m", n") и имеющих «форму», определяемую координатным шаблоном К(3, a,b).

Под поиском дубликатов по шаблону К ( 3 , a,b ) будем понимать задачу указания для каждого отсчёта ( m, n ) , определяющего начало фрагмента изображения с «формой», определяемой координатным шаблоном К ( 3 , a,b ) , уникального номера t ( m,n ) е N , характеризующего фрагмент следующим образом:

, , [ 0, нет дубликата t ( m , n ) = <  .

[> 0, номер « типа » дубликата

Под номером «типа» дубликата понимается некоторый уникальный номер, который оказывается одинаковым для совпадающих фрагментов (различающиеся фрагменты имеют различные номера).

Замечание 1 . Представление конкретного координатного шаблона может быть не единственным. В частности, шаблон вида к ( { ( 0,0 ) } ,10,10 ) определяет то же самое множество координат, что и шаблоны к ( { ( 0,0 ) , ( 1,0 ) } ,10,9 ) и к ( { ( 0,0 ) , ( 0,5 ) , ( 5,0 ) , ( 5,5 ) } ,5,5 ) . Эта неоднозначность представления в дальнейшем будет использована при построении алгоритма поиска дубликатов.

Хэш-функцией фрагмента изображения с «формой» , определяемой координатным шаблоном К ( 3 , a , b ) ( далее фрагмента изображения по шаблону), будем называть отображение вида:

T : в 81 ^{s ( 3 >} a , b )l__ _ n

., . ,8|К(3,a,b)| где N L < 2' 1 определяет множество возможных значений хэш-функции. По сути, хэш-функция переводит значения поля яркости конкретного фрагмента изображения (с определённым шаблоном) в некоторую целочисленную неотрицательную величину в диапазоне [0,L -1]. В работе авторов [5] были пред- ложены два способа построения хэш-функции для координатных шаблонов «прямоугольного» вида П( a, b,0,0). В частности, лучшим оказалась хэш- функция, использующая теоретико-числовое представление фрагмента изображения, задание которой производится следующим образом.

Пусть для получения хэш-значения используются все биты отсчётов координатного шаблона, тогда хэш-функция будет выглядеть следующим образом:

H ( m , n , f ) = f ( m , n ) • 2^{8( ab - 1)} +

+ f ( m , n + 1 ) ^ 2^{8( ab - 2)} + ... + f ( m + a - 1, n + b - 1 ) ^ 2⁰.

(1а)

Ввиду того, что выделить память для хранения таких значений невозможно на стандартных ПЭВМ, было предложено [5] использовать представление

H ( m , n , f ) в виде остатков от деления на R взаимно-простых чисел b r , r = 0, R - 1 (китайская теорема об остатках [7]). Тогда общий вид хэш-функции H r ( m , n , f ) выглядит следующим образом:

H r ( m , n , f ) = H r ( m , n , f ) mod b r .               (1б)

Указанная хэш-функция выступает в качестве прототипа для сравнения с предлагаемой ниже новой хэш-функцией. При этом сам предлагаемый алгоритм обнаружения дубликатов может быть использован вне зависимости от используемого варианта хэш-функции и описан в следующем разделе работы.

2.    Алгоритм обнаружения дубликатов по шаблону

Пусть решается задача поиска дубликатов по шаблону K ( 3 , a , b ) , представимому в виде (1). Предлагаемый алгоритм предполагает последовательный анализ всех возможных положений фрагментов П ( a , b , m , n ) изображения в режиме «скользящего окна» [6] . То есть при каждом положении ( m , n ) по значениям f ( m ‘ n ') , ,         соответствующего

'           'l ( m ', n ') еП ( a , b , m , n )

фрагмента изображения вычисляется значение хэш-функции, которое:

– используется для обновления хэш-таблицы H ( t ) , содержащей абсолютные частоты появления соответствующих значений t хэш-функции. Эта хэш-таблица фактически содержит отсчёты ненормированной гистограммы для хэш-функции;

– заносится в изображение потенциальных «типов» фрагментов T ( m , n ) .

Очевидно, что, поскольку в представлении (1) шаблона К ( 3 , a , b ) используется несколько «прямоугольных» шаблонов П ( a , b , m , n ) , анализируемый в позиции ( m ', n ‘ ) фрагмент изображения по шаблону К ( 3 , a , b ) может оказаться дубликатом только в том случае, если все |3| фрагментов вида

f (m'+m, n'+n )|                (m, n )e3

( m, n ) eH ( a , b , m , n )

оказались дубликатами. Таким образом, решающее правило отнесения фрагмента к определённому типу дубликата имеет вид:

,      [0, 3( m, n )e3 H (T (m + m, n + n ))< 1;t (m , n ) = <                                                        .

I T ( m , n ) + 1, e^ a-a.

Разработанный алгоритм в псевдокоде выглядит следующим образом:

FOR i=0 to M-1

FOR j=0 to N-1

BOOL isDuplicate = true;

t ( i , j ) = 0;

FOREACH ( m , n ) in 3

IF ( H ( T ( i + m , j + n ) ) < 1) isDuplicate = false;

BREAK;

END IF

END

IF (isDuplicate)

t ( i , j ) = T ( i , j ) + 1;

END IF

END

END

Можно заметить, что в силу неоднозначности построения представления (1) для конкретного координатного шаблона K ( 3 , a , b ) (см. Замечание 1 ) сам алгоритм также в общем случае определён неоднозначно. По этой причине в экспериментальных исследованиях, проведённых в настоящей работе, рассматривался ряд вопросов, касающихся оптимального (в смысле показателя качества) способа построения представления (1) для конкретного координатного шаблона.

3.    Эффективные линейные локальные признаки

Как можно видеть выше, значения хэш-функции являются результатами скалярного произведения значений отсчётов изображения и некоторого фильтра с конечной импульсной характеристикой – КИХ-фильтра. Для таких операций существует достаточно развитая теория построения эффективных КИХ-фильтров, позволяющих для конкретной задачи получить наилучший способ расчёта значений хэш-функции – линейных локальных признаков (ЛЛП) исходного изображения. В данном разделе представлено краткое изложение необходимых сведений и понятий из работ [8,9], опубликованных Мясниковым В.В.

Пусть K – алгебраическая система, имеющая свойства коммутативного кольца с единицей. В частности, в качестве K может выступать простое поле Галуа GF ( p ).

Линейным локальным признаком длины M над K

M -1                      _х1м -1

называется пара ( { h ( m ) } 0 , A I , где { h ( m ) } 0 - некоторая КИХ, задаваемая в виде конечной последовательности над K и удовлетворяющая ограничению h ( m ) ^ 0, h ( M - 1 ) ^ 0, а A - алгоритм вычисления свёртки произвольного входного сигнала над K с M -1

m ) } m =0 -

Представление последовательности

h ( 0 ) , h ( 1 ) ,..., h ( M - 1 ) над K в виде:

h ( m ) =

0,

K

^ akh (m - k ) + ф( m),

k =1

m < 0, m e Z+,

называется расширенным линейным рекуррентным соотношением (РЛРС) K-го порядка (K > 0). Отсчёты m e {n e Z+:Ф(n) ^ 0} называются отсчётами неодно родности РЛРС, множество O = { n e Z+ : ф (n )^ 0} -областью отсчётов неоднородности РЛРС, а вектор (M,K,{ak}K=1,{m,ф(m)} o) - вектором параметров РЛРС.

Рекуррентное вычисление ЛЛП (расчёт хэш-значений) для одномерных последовательностей f ( n ) в виде РЛРС имеет вид (обобщение для двумерного сигнала тривиально):

K

У (n) = ^акУ(n-k)+ ^ x(n-m)ф(m),n = 0,N-1. (*)

k =1 m eO

Алгоритм рекурсивного вычисления свёртки для одномерных последовательностей требует U, (K ) = 2K +1 умножений и U+ (K ) = 2K -1 сложе- ний на вычисление одного хэш-значения.

И х 1 M -1

m ) } _{m = 0} над K , представимая в виде РЛРС порядка K с областью неоднородности O , называется МС-последовательностью порядка K над K , если выполняется ограничение | O| = K + 1. МС-последовательность над K называет -ся нормализованной (НМС-последовательностью), если h ( 0 ) = 1 .

( K , M , a ) - семейством НМС - последовательностей , обозначаемым р ( K , M , a ) , называется множество НМС-последовательностей порядка K с носителем [ 0, M - 1 ] , удовлетворяющих РЛРС с коэффициентами a ( a_K ^ 0 ) . При этом количество НМС-последовательностей в семействе ограничено неравенством:

^ ( K , M , a )| < C M + K - ₂, V M >  K >  1, a ( a K ^ 0 ) .

В работах [8, 9] указан способ построения НМС-последовательности, который заключается в решении СЛАУ, содержащей M + K неизвестных. Вектор решения СЛАУ включает M значений КИХ - фильт- Их 1 M -1

m ) }    и K значений отсчётов неоднородности

'J m =0

ф ( m ) . СЛАУ выглядит следующим образом:

h (0) = 1,

K

h (m)- ^ akh (m - k) = 0, m e [1, M -1] / O,

k =1

K

^ akh (m - k) = 0, m e [M, M + K -1] / O,

k =1

K

h (m)- ^ akh (m - k )-ф( m) = 0,

k =1

m e [ 1, M - 1 ] A O ,

K

^ akh (m - k ) + ф( m) = 0,

k =1

m e[ M, M + K - 2] П ©, aKh (M - 1) + ф(M + K -1) = 0.

Частной задачей построения эффективного ЛЛП называется задача:

для заданных величин {ak}K=1 (aK ^ 0) N, M, K e N , удовлетворяющих ограничениям

N > M, K < N 2M +1 (M 4add), где 5add e R [0,1] - относительная сложность операций сложения, и заданного производящего функционала ^(...) опреде- лить ЛЛП

M -1

h m ,A m=0

такой что:

W M -1

n ) } 0 является НМС - последовательностью с минимальным значением целевой функции

• *(h⁽0),...,h⁽M^-1))^ min-1 ;

4.    Построение оптимальной хэш-функции с использованием эффективных ЛЛП

^{ h ⁽ m Я m =0

– алгоритм A является алгоритмом рекурсивного вычисления свёртки (*), порождаемой последова-

W M -1

n ) } 0 .

Для поиска неискажённых дубликатов на изображении будем решать СЛАУ (3) в простом поле Галуа GF ( p ) . Характеристикой поля в этом случае является простое число p , и все необходимые арифметические операции в ПЭВМ при решении СЛАУ и вычислении хэш-значений будут производиться по модулю p .

Коэффициенты СЛАУ { a k } K =1 будем определять одним из следующих способов:

• A.    элементы последовательности Фибоначчи:

• •    K = 2, a 1 = 1, a ₂ = 2 ;

• •    K = 3, a 1 = 1, a ₂ = 2, a ₃ = 3 ;

• •    K = 4, a 1 = 1, a ₂ = 2, a ₃ = 3, a ₄ = 5;

• B.    полиномиальные коэффициенты:

• ak = (-1)kNK .

5.    Экспериментальные исследования

Выбрав коэффициенты для заданного значения K , а также задав длину КИХ-фильтра M , строим СЛАУ (3) для каждой возможной НМС-последовательности из соответствующего семейства ^ ( K , M , a ) .

Как было указано выше, количество различных вариантов построения СЛАУ (3) (НМС-последовательностей) равно NM+1K-2 [8]. В силу доказанных в [8] свойств решения частной задачи одно из решений гарантированно будет обладать минимальным значением целевой функции, то есть являться наиболее эффективным. Поскольку решения СЛАУ (3) дают одномерные КИХ-фильтры {h (m)} , дву- m =0

мерный КИХ-фильтр M х M может быть получен путём декартова произведения одномерного КИХ-фильтра h и его транспонированного значения hT .

Замечание 2 . Хэш-функция (1а)-(1б) также может быть представлена с использованием эффективных ЛЛП. В частности, она соответствует семейству р ( K , M , a ) с параметрами K = 1, a 1 = 2⁸ и остатком b r = p . Заметим, что для такого конкретного случая |^ ( 1, M , a )| <  C M -1 = 1, то есть наилучшая в смысле значения целевой функции НМС-последовательность оказывается единственной.

Исследование эффективности предложенной хэш-функции

Ключевым параметром предложенной хэш-функции является количество неоднородностей K . В качестве показателя качества для всех проводимых в данном разделе исследований будем использовать количество ложно найденных дубликатов, или коллизий . Получаемые результаты сравним с решением на базе КТО [5] (как было показано в Замечании 2, это решение соответствует ситуации при K =1).

В качестве исходных данных для эксперимента были выбраны 3 изображения, полученные со спутника SPOT-4, с размерами 4600 х 6400 , дубликаты на которых отсутствовали. При выбранной длине одномерного КИХ-фильтра M = 11 сначала фиксировалось значение K = 2, 3, 4 и способ вычисления коэффициентов { a k } K =1 , а затем для каждого значения K строились и решались N MM ₊ K _{- 2} СЛАУ (3). Учитывая, что вычисления проводятся в GF ( p ) , в качестве его характеристики было выбрано простое число p=536870923 , что соответствует полученным ранее результатам для алгоритма на основе КТО, где выбиралось простое число p , близкое к 2²⁹ . Каждый полученный КИХ-фильтр применялся к выбранным изображениям для определения наилучшего вектора параметров, при котором количество коллизий минимально. Эффективность фильтров сравнивалась с результатами, полученными для хэш-функции (ХФ) на базе КТО, для окна обработки с размерами 11 х 11 -результаты представлены в таблице 1. При K = { 3,4 } алгоритм вычисления хэш-функции на основе ЛЛП показал лучшие результаты по сравнению с алгоритмом на основе КТО.

Таблица 1. – Сравнение количества коллизий для значений хэш-функций при фиксированных K

K	Число коллизий		Положения неоднородностей		ХФ на основе КТО
	A	B	A	B
2	7757353	12076155	11	1	1550186
3	1550085	1550108	1,7	3,12	1550186
4	1548417	1547133	4,11,13	1,4,7	1550186

В продолжение этого исследования мы проанализировали поведение предложенного алгоритма поиска дубликатов, описанного в разделе 2. В качестве координатного шаблона был выбран следующий шаблон: К ({(0,0), (0,1), (1,0), (1,1)}, 11,11), а вектора параметров РЛРС соответствовали наилучшим КИХ-фильтрам, полученным во время предыдущего эксперимента. В результате проведённых исследований было получено, что алгоритм обнаружения на основе ЛЛП даёт меньшее число коллизий для K = {3,4} с использованием обеих схем вычисления коэффициентов { a k } K =1 по сравнению с алгоритмом на основе КТО (таблица 2).

Таблица 2. – Сравнение числа коллизий алгоритма обнаружения дубликатов на основе хэш-функций с ЛЛП

K	Число коллизий		Алгоритм на основе КТО
	A	B
2	240854	1338933	235
3	242	230	235
4	232	225	235

Как показало данное исследование, хэш-функция, конструируемая с использованием эффективных ЛЛП, позволяет получить лучший результат (по качеству), чем хэш-функция на базе КТО. В то же время расчёт хэш-значения на ПЭВМ для подхода с использованием ЛЛП занимает чуть больше времени – улучшенные качественные показатели достигались за счёт 20-25% потерь во времени обработки.

Исследование способов представления используемого координатного шаблона

В рамках настоящего исследования рассматривались два вопроса:

– о выборе оптимального количества элементов в представлении (1), то есть об оптимальной мощности множества | 3 |;

– о наилучшем способе представления (1). В данном случае наиболее интересны два альтернативных способа представления (1) для заданной мощности 1 3 |: с наибольшим возможным парным пересечением множеств П ( a , b , m , n ), ( m , n ) e3 , входящих в представление (1), и с наименьшим.

Рассмотрим использование двух вариантов окон обработки анализируемого изображения: 11 x 11 (| 3 | = 4 ) и 18 x 18 (1 3 | = 9). Параметры координатного шаблона a x b будут варьироваться от минимально возможного (для алгоритма с минимальным пересечением составляющих шаблона) до максимального. Тогда графики изменения количества коллизий алгоритма поиска дубликатов будут выглядеть, как показано на рис. 1 и рис. 2.

Из графиков видно, что количество коллизий существенно растёт с уменьшением области пересечения множеств П ( a , b , m , n ), ( m , n ) e3 , а оптимальный размер параметров шаблона составляет от

8 x 8 до 10 x 10. Также можно отметить, что число коллизий тем меньше, чем больше мощность множества 1 3 |.

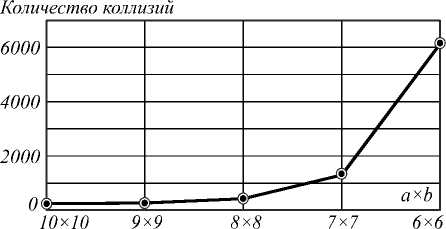
Рис. 1. Зависимость количества коллизий от параметров a x b шаблона для окна анализа 11 x 11

Количество коллизий

9-----------------(	)                   (	5--------------------(	)                6		’ охЬ

16x16 14x14 12x12 10x10   8x8   7x7 6x6

Рис. 2. Зависимость количества коллизий от параметров a x b шаблона для окна анализа 18 x 18

В ходе исследований был также получен следующий результат для окна обработки с размерами 19 x 19, 1 3 1 = 4 (рис. 3).

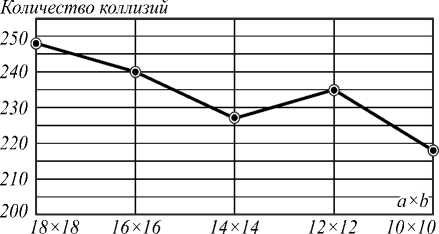
Рис. 3. Зависимость количества коллизий от параметров a x b шаблона для окна анализа 19 x 19

На рисунке видно незначительное уменьшение количества коллизий от уменьшения размера координатного шаблона. В сравнении с результатами на рис. 1 и 2, в данном случае (параметры a x b шаблона принимают значения б о льшие 10) число коллизий можно считать постоянным, а при увеличении мощности множества 1 3 | - стремящимся к 0.

По полученным результатам второго исследования можно сделать следующие выводы, связанные с выбором оптимальных/наилучших параметров координатного шаблона и, как следствие, алгоритма обнаружения дубликатов:

– наилучшими параметрами a и b шаблона являются значения не меньше «8»;

• -    мощность множества | 3 | не должна быть меньше «6» (рекомендуемая – «9»);

  – «степень» взаимного наложения составляющих шаблона не оказывает существенного влияния на результат обработки, если выполнены предшествующие два пункта.

Выводы и рекомендации

В данной работе был представлен новый алгоритм поиска неискажённых дубликатов на изображениях. Предложен новый способ вычисления хэш-функции, основанный на использовании ЛЛП. Предложенное решение показало лучшие результаты по количеству коллизий в сравнении с существующим решением на основе КТО. Даны рекомендации по выбору параметров алгоритма обнаружения – параметров координатного шаблона a , b, мощности множества | ℑ | и способа представления используемого координатного шаблона.

Дальнейшие исследования будут направлены на разработку алгоритма на базе ЛЛП в рамках поля R для поиска яркостно-искажённых дубликатов на цифровых изображениях.

Работа выполнена при финансовой поддержке:

• -    грантов РФФИ, проекты № 13-07-12103-офи-м, 13-01-12080-офи-м, 12-07-00021-а;

• -    программы фундаментальных исследований Президиума РАН «Фундаментальные проблемы информатики и информационных технологий», проект 2.12;

• -    Министерства образования и науки Российской Федерации в рамках постановления Правительства Российской Федерации от 09.04.2010 г. № 218: договор № 02.Г36.31.0001 от 12.02.2013.