Алгоритм обнаружения искажённых дубликатов на цифровых изображениях с использованием бинарных градиентных контуров

В эпоху цифровых технологий невозможно представить себе более популярного средства представления и передачи информации, чем цифровые изображения и видео. Они используются во всех сферах жизнедеятельности и имеют приложение во многих отраслях науки и техники. Так, фотографии применяются повседневно в СМИ, социальных сетях, облачных сервисах хранения данных. Согласно статистике [1], в 2015 году в известной социальной сети Facebook ежедневно загружалось в среднем 300 миллионов цифровых изображений. Следует учесть, что в последние несколько лет появилось огромное количество веб-приложений (Instagram, Twitter, Flickr и т.д.), которые ежедневно осуществляют сопоставимый с Facebook трафик цифровых изображений. Такой колоссальный объём данных не может не интересовать злоумышленников, потому что человеку свойственно сначала воспринимать информацию как она есть, а затем уже подвергать её критике. В зависимости от содержащейся в цифровом изображении информации, она может быть использована в компрометирующей форме и привести к серьёзным политическим и экономическим последствиям, если контрафактность данных не будет обнаружена. Именно поэтому в современном мире цифровые данные должны быть как можно лучше защищены от изменений злоумышленниками, чтобы не быть лёгким оружием в информационном противостоянии.

Одним из самых часто используемых способов подделывания изображения является копирование и вставка области этого же изображения. Такие атаки называются дублированием фрагментов цифрового изображения, а копируемые области – дубликатами. Между копированием и вставкой к дубликату могут применяться различные преобразования: геометрические (масштаб, поворот), яркостные (контрастирование, добавление шума) и другие. Такие дубликаты будем называть искажёнными. В рамках данной работы под искажениями будем понимать изменения, возникающие в результате линейного контрастирования, внесения аддитивного шума, компрессии. Очевидно, что внесение изменений в копируемый фрагмент изображения приводит к усложнению обнаружения данного вида атаки.

В настоящее время существует большое количество работ, посвящённых разработке алгоритмов обнаружения искажённых и неискажённых дубликатов: общим в них является разработка некоторых признаков, инвариантных к вносимым в ходе преобразований искажениям, вычисляемых для положений скользящих окон с перекрытиями [2]. Ранее авторами работы были разработаны алгоритмы обнаружения неискажённых дубликатов, в основе которых лежали вычисление значений хэш-фукнций в скользящем окне и дальнейший поиск одинаковых значений при помощи хэш-таблицы [3–5]. Предложенные решения показали высокую эффективность при низкой вычислительной сложности.

Существующие алгоритмические решения по обнаружению искажённых дубликатов могут быть разбиты на пять основных групп [2]:

• 1)    алгоритмы на основе вычисления моментных признаков (Blur [6], Zernike [7]);

• 2)    алгоритмы на основе признаков снижения размерности (PCA [8], SVD [9]);

• 3)    алгоритмы на основе анализа локальных яркостных характеристик (Luo [10], Bravo [11]);

• 4)    алгоритмы на основе анализа частотных характеристик (DCT [12], FMT [13]);

• 5)    алгоритмы, определяющие ключевые точки на изображении (SIFT [14], SURF [15]).

Предлагаемый в данной работе алгоритм относится к группе алгоритмов, использующих для поиска дубликатов признаки, вычисляемые на основе анализа локальных яркостных характеристик (группа 3). Одним из способов вычисления локальных яркостных характеристик является построение локальных бинарных шаблонов (ЛБШ, Local Binary Pattern ). ЛБШ ранее уже использовались для обнаружения искажённых дубликатов [16–17]. Тем не менее в работе по классификации текстур [18] было отмечено, что ЛБШ являются неустойчивыми к шуму и необходимо использовать более устойчивые вариации локальных шаблонов для построения признаков, инвариантных к разного рода искажениям.

В данной работе мы предлагаем новый алгоритм обнаружения искажённых дубликатов на основе вычисления признаков с использованием бинарных градиентных контуров (БГК), предложенных в работе [19] A. Fernández и коллективом соавторов для решения задачи классификации текстур. БГК являются модификацией ЛБШ, и их использование позволяет с высокой точностью обнаруживать дубликаты с внесёнными искажениями, что подтверждается результатами экспериментальных исследований.

Работа построена следующим образом. В первом пункте дано описание ЛБШ и его распространённых форм, используемых для повышения устойчивости к искажениям: стандартный ЛБШ, устойчивый к повороту ЛБШ, полный ЛБШ и его модификация, устойчивый ЛБШ и локальный тернарный шаблон (ЛТШ). Второй пункт работы посвящён описанию трёх форм БГК, которые будут применяться в работе. Третий пункт посвящён описанию алгоритма обнаружения дубликатов, в рамках которого используются новые признаки на основе БГК. В четвёртом пункте приводятся результаты экспериментальных исследований разработанного алгоритма обнаружения искажённых дубликатов в зависимости от параметров вносимых искажений.

1.    Локальный бинарный шаблон и его разновидности

Локальный бинарный шаблон

ЛБШ является достаточно известным и часто используемым в распознавании образов локальным признаком цифровых изображений. Этот вид локальных признаков привлекает внимание исследователей благодаря низкой вычислительной сложности, инвариантности к равномерному изменению яркости и способности описывать текстуры [20, 21]. На практике оператор ЛБШ совмещает свойства статистического и структурного текстурного анализа, позволяя строить дескрипторы цифровых изображений.

Идея ЛБШ принадлежит Wang [20], и была позднее развита Ojala и коллективом соавторов в работах [21, 22], где шаблон использовался в задачах классификации. Впоследствии ЛБШ получили широкое применение в обнаружении и распознавании лиц, в обнаружении движущихся объектов и в других областях анализа цифровых сигналов. Под ЛБШ понимают некоторое описание окрестности пикселя в бинарной форме. В базовой версии для построения ЛБШ использовалось окно 3×3 в окрестности центрального пикселя. 8 соседних значений сравнивались с цен- тральным, и в зависимости от результата сравнения центральному пикселю ставилось в соответствие 8битное число, которое называется кодом ЛБШ (рис. 1) (в данном случае значению “0” соответствует

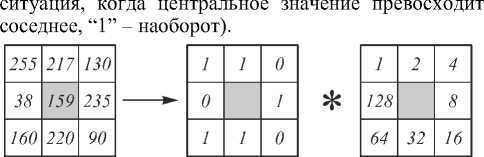
Окрестность        Применение         Весовые

3x3            предиката      коэффициенты

Рис. 1. Базовая версия ЛБШ.

Код ЛБШ – 1+2+8+32+64=107

По аналогии с этим алгоритмом в дальнейшем стали использоваться более широкие окрестности центрального пикселя для построения кода (рис. 2).

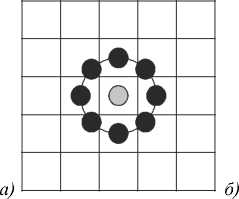
Рис. 2. Центрально-симметричные окрестности пикселя для различных пар значений (P, R): а) (8, 1) и б) (16, 2)

Определим изображение как функцию яркости пикселя f ( x , y ). Пусть также определён бинарный вектор b длины P :

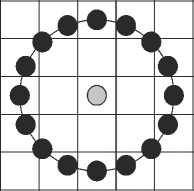
b = ( b 0 ,..., b p - 1 ) , b i e В , В = { 0,1 } .

Определим далее для центрального пикселя f c = f ( x c , y c ) P равноудалённых соседей f i = f ( x i , y i ), i = 0, P - 1 , расположенных на окружности радиуса R . Тогда код ЛБШ определяется следующим образом:

p - 1                      p - 1

LBP p , R ( X c , У с ) = £ I ( f >  f c ) . 2 i = £ b i • 2 i , (1) i = 0                          i = 0

где I – индикатор события, определяемый следующим образом:

• 1 1, n = true ,

I (n) = 1

• [ 0, n = false .

В терминах, введённых в работе В.В. Мясникова [23], выражение (1) называется строгим кодовым преобразованием, так как приводит к взаимно-однозначному переводу бинарной последовательности в целочисленное значение. Так, например, для 8-компонентного вектора b имеем 256 различных значений кодов ЛБШ. Как было описано в работе [18], такое преобразование является чувствительным к шумовым искажениям (квантование вследствие округления при контрастировании, добавление шума и др.), при этом границы чувствительности можно указать явно [23]. Ввиду проблемы чувствительности ЛБШ в прикладных задачах часто используются другие формы ЛБШ, которые будут описаны далее в этом разделе.

Стандартная форма шаблона

Одним из способов решения проблемы чувствительности ЛБШ к шумовым искажениям является использование стандартных ЛБШ (Uniform LBP) [24], отличающихся повышенной устойчивостью к указанным выше искажениям. Стандартные ЛБШ позволяют выявлять локальные примитивы, такие как: контура (edge), пятна (spot), углы (corner). Дадим определение кода стандартного ЛБШ. Для этого введём несколько понятий.

Определим функцию количества переходов для бинарного вектора b :

P - 2

U ( b ) = X I ( b . b_M )                        (2)

i = 0

Кодом стандартного ЛБШ будем называть код ЛБШ следующего вида:

' P - 1

LBP U, r ( x , У с ) = ‘

X I ( f >  f c ) ■ 2 i , U ( b ) < 2,

I = 0

P ■ ( P - 1 ) + 3, иначе .

Примерами стандартных ЛБШ с параметрами ( P , R ) = (8,1) являются битовые вектора 11000111 , 11111000 , 00000000 . Исходя из определения, для P-битного вектора b количество кодов стандартного ЛБШ LBP P_R составляет P ■ ( P -1)+3. Достаточно очевидно, что стандартные ЛБШ не являются строгими кодовыми преобразованиями. В частности, если для ЛБШ с параметрами ( P , R ) = (8,1) имеем 256 различных кодов, для стандартного ЛБШ имеем только 59 кодов. Такое уменьшение числа кодов позволяет снизить количество ошибок, возникающих вследствие шумовых искажений, но при этом ведёт к росту числа коллизий (ложно обнаруженных дубликатов).

Форма стандартного шаблона, устойчивая к повороту

В работе [22] приводится также устойчивая к повороту форма стандартного ЛБШ, в основе которой лежит выбор минимального значения кода стандартного ЛБШ среди всех его циклических сдвигов. Пусть для некоторого положения ( x c , y c ) получен код стандартного ЛБШ LBP P_R ( x c , y _c ) , тогда код устойчивого к повороту стандартного ЛБШ вычисляется следующим образом:

_R1U .     .   [ min W ( LBP^_r , k ), U ( b ) < 2

LBP PRU ( X c , y c ) = j k         P ^, R             , (4)

[ P +1, иначе где W(LBPPUR, k) - функция циклического сдвига ко- да стандартного ЛБШ на k бит влево. Преобразование (4) приводит к формированию только P+1 различных значений кодов.

Полная форма шаблона

Отличительной особенностью другой формы ЛБШ, называемой полной [25–26], является аккумулированное описание локальной структуры изображения с использованием трёх составляющих: знаковой, амплитудной и центральной. Эти компоненты могут быть использованы в любой комбинации для построения расширенного кода.

Знаковая составляющая CLBP_S P,R представляет из себя код ЛБШ вида (1). Амплитудная составляющая представляет из себя ЛБШ, код которого вычисляется следующим образом:

p - 1

CLBP _ M p , R ( X c , y c ) = ^ I (| f - f c | >  E _M ) ■ 2 i , (5) i = 0

где E M – среднее значение амплитуд | f i – f c |. Центральная составляющая позволяет учитывать значение центрального пикселя f c при построении кода, и её код, соответственно, выглядит следующим образом:

CLBP _ С P , R ( X c , y c ) = I ( f c >  E f ) ,               (6)

где E f – среднее значение изображения f .

Модификация полной формы шаблона

Другим подходом к построению кодов полного ЛБШ является использование вместо центрального значения f c различных преобразований [26]:

p - 1

X ( f + f c )

ALG ( f c ) = ^=0 ^ +1---,                     (7)

P - 1

X ( f cj + a f c )

WLG ( f c ) = -j ⁰-;-------,                    (8)

P + a где fcj – равноудалённые соседние пиксели для пикселя fc, os N. Выражение (8) может быть, например, использовано при вычислении амплитудной составляющей CLBP_MP,R (5) путём замены |fi–fc| на следующее выражение:

m i = WLG ( ( f ) - WLG ( f c )[                      (9)

Устойчивый локальный бинарный шаблон

Авторы работы [18] предлагают использовать УЛБШ для устранения в процессе формирования кодов шумов, возникающих при небольших отклонениях соседних пикселей от центрального. Для этого вводится некоторое пороговое значение, которое приводит к возникновению дополнительного неизвестного состояния бита кода, как показано далее.

Пусть задано некоторое пороговое значение t e Z , и величина А обозначает некоторое незаданное (неизвестное) значение из B . Для построения неполного кода ЛБШ введём следующую функцию П : Z ^ B u { A }:

[ 1, x 2 t ,

П ( x ) = М,| x <  t ,                                (10)

[ 0, x < - t .

В случае, если П( x ) e {0,1}, то будем считать разницу между значениями пикселей значимой. В противном случае (П( x )= А ) разница считается неизвестной (малая разница между значениями наиболее подвержена влиянию шума). В этом случае неоднозначный бинарный вектор будем обозначать следующим образом:

C ( x c , У с ) = ( b о , b l ,..., b p - 1 ) b i = П ( f - f c ) .       (11)

Следующим этапом процедуры построения УЛБШ является определение его бинарного вектора таким образом, чтобы шаблон принял стандартный вид. Эта задача решается путём последовательного перебора неизвестных значений в C ( x c , y c ). Следует учитывать то, что из одного неоднозначного бинарного вектора можно сформировать несколько ЛБШ стандартного вида (рис. 3). Например, на основе неоднозначного бинарного вектора вида 11v1v0v0 могут быть получены следующие стандартные ЛБШ: 11110000 и 11111000 .

Рис. 3. Формирование УЛБШ (t=2)

Ввиду того, что неопределённый вектор может порождать несколько стандартных ЛБШ, в [26] предлагается алгоритм построения признаков на основе вычисляемых кодов.

Пусть для изображения f определено скользящее окно обработки с размерами M 1 * M 2 W^ , k e [0, N 1 - M 1 ], l e [0, N 2 - M 2 ], где k, l - координаты верхнего левого пикселя окна, а N 1 × N 2 – размеры изображения. Пусть также задано множество всех стандартных ЛБШ S C , получаемых из неоднозначного бинарного вектора C . Тогда алгоритм построения вектора признаков для W k,l с использованием УЛБШ выглядит следующим образом:

Шаг 0. Для всех скользящих окон обработки W k,l вычислить неоднозначный бинарный вектор C ( x c , y c ) (11). Шаг 1. Сформировать для каждого C ( x c , y c ) множество S C ( x_c , y_c ) .

Шаг 2. Добавить элементы t e S с ( x_c , y_c ) в гистограмму значений стандартных кодов (вектор признаков) h w ( t ) e R следующим образом:

^h w ^{( t ) +} 1, ^S с ( x c , y c ) = ⁰

h ( t ) =                   1               .

W      I h W ( t ) + 1---------p, иначе

[              ^S C ( x c , y c )

Локальный тернарный шаблон

ЛТШ является расширением ЛБШ и позволяет задавать три различных значения при построении кода, учитывая знак разницы соседних пикселей от центрального.

Пусть t e Z - некоторое пороговое значение, тогда код ЛТШ определяется следующим образом:

LTPp _R {x_c , y_c ) = Vf I ^{( f} " ^{f c} "  t ) J• 3 i .     (12)

P,RYc^c) ^-1(   f <-1)J i=0

ЛТШ также отличает повышенная устойчивость к искажениям в связи с учётом знака, что отсутствует в ЛБШ. При этом количество возможных кодов ЛТШ при строгом кодовом преобразовании составляет 3⁸ =6561 (при P =8, R = 1). Для снижения количества кодов ЛТШ может быть представим в виде двух ЛБШ вида (1): p - 1

LBPPr ( x_c , У_с ) = Z I ( f i - f_c ^ t ) • 2 ‘ ,

P -                                (13)

LBPp²r ( x c , y c ) = Z I ( f - f= >- 1 ) • 2 ‘ . i = 0

В таком случае для анализируемого блока строится два кода ЛБШ, которые в дальнейшем используются одновременно в процессе обнаружения дубликатов.

Следует также отметить, что все описанные выше формы ЛБШ справедливы и для ЛТШ и вводятся аналогичным образом.

• 2.    Бинарные градиентные контура

БГК ( Binary Gradient Contours ), предложенные Fernández, A. и коллективом соавторов в работе [19], относятся к классу дескрипторов, основанных на попарном сравнении значений пикселей, выбираемых из некоторой окрестности (далее будем использовать окрестность 3×3) по заранее определённому правилу или маршруту. Очевидно, что количество различных вариантов построения БГК определяется правилами обхода пикселей окрестности. В работе [19] предлагается 3 способа построения БГК.

Первые два способа используют один обход всей окрестности центрального пикселя для генерации кода (обход пикселей для всех способов ведётся по часовой стрелке). В качестве пути обхода пикселей для первого способа применяется последовательность вида {0, 1,2,3,4,5,6,7,0}, где «0» соответствует индексу верхнего левого пикселя окрестности. Код БГК в этом случае вычисляется следующим образом:

BGC ¹ ( x c , y c ) = Z I ( f i - f '} + 1 ) mod8 ^ 0 ) ^ 2 ⁱ . (14) i = 0

Второй способ основан на обходе пикселей по маршруту вида {0, 3,6, 1,4,7,2,5,0}. Код БГК в этом случае выглядит следующим образом:

• 7^ f f -      ^

BGC ² ( x c , y c ) = У 1 1 7 _>nl • 2 i .    (15)

^ ( ^{- f} 3 ( i + 1 ) mod8 2 ⁰ i = 0

Оба способа генерируют 28–1 возможных вариантов кодов.

Третий способ генерации кода БГК отличается от предыдущих использованием двух отдельных маршрутов: {1, 3, 7, 5, 1} и {0, 2,4, 6, 0}. Каждый маршрут позволяет создать 24–1 различных кодов, а их совместное использование, очевидно, приводит к (24–1)2 различным кодам. Выражение для данного способа генерации кода БГК выглядит следующим образом:

• BGC ³ ( x c , y_c ) =

• = ( 2 4 - 1 ) . £ I ( f 2 - f ₂ ( i _{+ 1} ) _m od8 >  0 ) . 2 i +         (16)

• i = 0

• + £ I(f 2i+1 — f :2i+3)mod8 > О)’ 2- 24.

3.    Алгоритм обнаружения дубликатов

i = 0

В данном пункте будет представлено описание алгоритма обнаружения дубликатов с использованием признакового описания. В основе признакового описания лежит вычисление значений кодов шаблонов. Алгоритм состоит из следующих этапов:

• 1.    Формирование векторов признаков.

• 2.    Поиск близких векторов признаков.

• 3.    Постобработка с целью снижения ошибок обнаружения.

Формирование векторов признаков

Пусть для изображения f определено окно обработки W k,l с размерами M 1 × M 2 , как в предыдущем разделе. Пусть также задано смещение окна s e N (для скользящего окна s = 1). Количество окон обработки изображения будет вычисляться следующим образом: