Алгоритм обработки изображений при фотограмметрических измерениях

Наиболее часто при проведении фотограмметрических измерений используют стереоскопические фотоаппараты (неметрические фотокамеры). При этом делается два снимка одинаковыми объективами, выставленными в определенных направлениях.

Для вычисления результатов измерения в трехмерных координатах полагают следующие допущения [1]:

• -    точки размещения фотокамеры по горизонтальной оси симметричны ( х ₁ = 0,5 b ; y = 0; z = 0 и x ₂ = –0,5 b ; y = 0; z = 0; b – расстояние между центрами осей фотоаппаратов при съемке);

• -    оптическая ось фотоаппарата параллельна вертикальной оси z измерительной системы координат;

• -    оси x и y систем координат снимка и измерительной системы совпадают;

• -    отсутствуют искажения геометрии изображения (дисторсия).

Координаты точки объекта x , y , z определяются из подобия треугольников [1] путем нахождения координат отображений u и v на первом и втором снимках.

Решая систему уравнений (1), находим координаты точки объекта:

-Y = - - • (11 _v + M₂ ) ' — = - ■ (^ + «₂ )--i

2         j 2         u7- uv b-f .

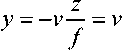
Разность u ₂ – u ₁ называется параллаксом точки; f – фокусное расстояние от центра объектива до плоскости изображения.

Постановка задачи

При использовании бытового фотоаппарата с неметрической камерой необходимо выпол- нить несколько снимков с разных положений и учесть координаты (XC, YC, ZC) и ориентацию (углы Эйлера: CO, к, ф) фотоаппарата в пространстве.

Трехмерные координаты и система уравнений (1) трансформируются в систему координат (СК), связанную с положением фотоаппарата, номером снимка k и номером точки i :

AX' -X^m^ -YcHA^ -Z^k_cH ⁷ (T -X>^k_zx +(У -Y^k>^k_zy ^Z -x^kM ’

k_cV_yx +(У -Y^kV_yy ^(Z -Z^k_cV_yz ⁷ (Г -X>t_x +(У -Yl)< -az -Z>L ■

Здесь коэффициенты m^k_xx , m^k_xy , m^k_xz , m^k_yx , m^k_yy , m^k_yz , m^k_zx , m^k_zy , m^k_zz – компоненты матрицы поворота M [2], определяемые углами co. ^, ф^к;

СО§ф-СО8К

м =

-cos^-sin/c

sin^

cos co • sin к + sin co ■ sin ф • cos к sin к ■ sin co - cos co • sin ф • cos к cos к • cos co - sin co • sin ф • sin к cos к • sin co + cos co • sin ф • sin к -sinty-cos^                  cos^-cos

Для определения координат различных точек на различных снимках необходимо осуществить преобразование СК. При преобразовании необходимо учитывать вид преобразования и измеренных параметров. В зависимости от этого различают следующие варианты.

• 1.    Преобразование одной СК в другую с использованием следующих сочетаний различных шести параметров:

• -    начало координат ( X_C , Y_C , Z_C ) и углы Эйлера ( co, к, ф) ориентации фотоаппарата в пространстве;

• -    вектор начала координат Х и базисные вектора Ех Еz по осям х и z ;

• -    углы ориентации CD, К, Ф в пространстве, определяющие матрицу поворота M [2].

• 2.    Преобразование координат из внешней СК осуществляется [2] согласно системе уравнений:

• 3.    Если две СК (СК1 и СК2) определены во внешней СК: (СК1: X_C1 , M ₁ ; СК2: X_C2 , M ₂ ), то преобразование из СК1 в СК2 будет иметь вид:

x’ = (x-X_c )m_xx + (V - Y_c )m_xy + (z - Z_c )m_xz;

v = {x-X_c)m_yx + (y-Y_c')m_)y +(z - Z_c)m_yzA4) z' = (x-X_c )m_zx + (y - Y_c >_zy + (z - Z_c )m_zz.

Величины m_xx , m_xy … m_zz – компоненты матрицы поворота M [2]. В векторном виде x = M(x-X_c) ; обратное преобразование x = X_c +M x .

x" = M₂(X_Ci+M^kx'-X_C2) . Взаимосвязь СК2 и СК1 определяется: M₂,=M₂Mf; Х_С2|=М₂(Х_С2ад. По компонентам матрицы M _{2 i} определяются угловые параметры ориентирования ®2Ь ^21,^21 при переходе из СК2 в СК1.

Измерения размеров объектов сводятся к определению координат изображений одних и тех же точек объекта на разных снимках и решению системы уравнений (3). Определяются трехмерные координаты точек объекта и положения фотоаппарата в момент съемки. Важным моментом при обработке информации является наличие необходимого числа опорных точек с известными трехмерными координатами.

Решение задачи

Рассмотрим возможные варианты решения системы уравнений (3) с известным f .

• 1.    Изображения одной и той же точки предмета, измеренные на двух снимках с известными параметрами ориентирования X_C , Y_C , Z_C , co, к, ф дают 4 уравнения, по которым можно определить трехмерные координаты точки ( X , Y , Z ).

• 2.    Три точки с известными трехмерными координатами, измеренными на одном снимке, дают 6 уравнений. Можно определить параметры ориентирования снимка X_C , Y_C , Z_C , co, к, ф (внешнее ориентирование снимка).

• 3.    Для пары снимков можно выбрать общую внешнюю систему координат, в которой уравнения имеют простой вид (1)-(2) (базисная система координат); сами изображения приводятся в эту систему координат проективным преобразованием плоскости. Преобразованные изображения образуют стереопару, по ней удобно выполнять измерения, можно наблюдать стереоизображение. Базисную систему координат можно определить по известным параметрам внешнего ориентирования снимков X_C , Y_C , Z_C , О), к, ф.

• 4.    Пять точек с неизвестными трехмерными координатами, измеренные на двух снимках, дают 5×2×2–5×3 = 5 уравнений. Можно определить угловые положения одного снимка относительно другого и, следовательно, положения снимков относительно базисной системы координат этой пары снимков с точностью до расстояния между точками съемки (взаимное ориентирование пары снимков). Положение базисной системы координат относительно СК объекта остается неизвестным. По связанной таким образом паре снимков можно выполнить трехмерные измерения с точностью до масштаба.

При использовании неметрической фотокамеры требуется учесть ее внутренние параметры:

• -    положение главной точки u _M , v _M , то есть проекцию оптического центра объектива на плоскость изображения (она не обязательно совпадает с центром кадра);

• -    реальные фокусные расстояния по вертикали и горизонтали кадра (неквадратные пиксели) f _U , f _V ;

• -    нелинейные геометрические искажения, которые можно представить в виде разложения поправок по степеням измеренных на снимке координат [3-7]:

и = u + Dr,,,u + Db,_uvvuv +... , v' = v + Dv_m.y3 + Dvvuuvir +... , где ^U_UUU’ ^v_vvv – коэффициенты дисторсии.

В данном случае необходимо решение системы уравнений:

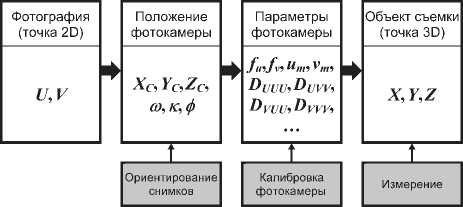
Структура решения уравнений (6) может быть представлена в виде, показанном на рис. 1. Систему (6) предлагается решать по частям.

• 1.    Калибровка фотокамеры. Требуемые параметры камеры определяются заранее по снимкам калибровочных объектов с известной геометрией, предполагается, что параметры камеры сохраняются во время рабочих измерений. Возможно уточнение параметров по рабочим снимкам.

  

• 2.    Ориентирование снимков. Выполняется связывание снимков по известным опорным точкам и, возможно, по некоторым точкам измеряемого предмета. Используются хорошо опознаваемые и надежно измеряемые точки. Оценивается точность полученной стереомодели.

• 3.    Измерение точек предмета. Для удобства измерений могут формироваться стереопары.

Рис. 1. Структура решения уравнений

Заключение

В ходе работы были проведены измерения концевых мер вышеописанным способом. Концевые меры – это метрологические устройства, предназначенные для точного измерения геометрических размеров объектов, их метрологический параметр, в нашем случае – толщина, нормирован и подвергается периодической аттестации. Для проведения испытаний были взяты четыре типа мер с толщинами 6; 7; 8 и 9 мм. Тестовые объекты были сфотографированы в приспособлении, их фотографии подвергнуты обработке с помощью специального программного обеспечения (см. рис. 2). Контрольные точки устанавливались как на переднем плане фотоснимков, так и на заднем. Результаты измерений представлены в таблице 1.

^Uik ^MM ⁺ ^U_UUU^UA ⁺ ^U_UVV^Uik^Vik + ••• -

(X' -X^k_cW_xx + (F - Гс )< + (^' - ^ZcК .

L (X‘-Хь)ткх + (Y' -Yk>ky+(Z- -ZkVzz ’

3                                                            ((

^Vik ^{- v}m + ^Dv_vvv^Vik ^{+ D}v_vuu^Vik^Uik + ••• =

(X- -Хкс>к^(У -Yk>ky+(Z‘-Zkc)rnkz

{X'-X^mkzx+(Yi-Yk)mkzx+{Zi-Z>kzz •

Таблица 1. Результаты измерений концевых мер

	ю сЗ О 5	оЗ CI. S	оЗ 5	^ сЗ о 5
Размеры меры, мм	5,996	6,997	7,999	8,999
Результаты измерений, мм	6,005	7,080	7,958	9,092
Погрешность, мм	0,009	0,083	0,041	0,093

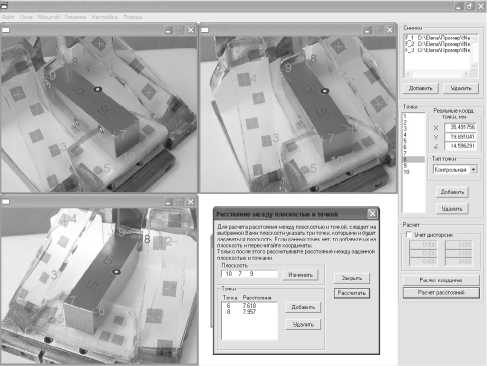
Рис. 2. Измерение концевых мер

Как видно из таблицы 1, погрешность измерения не превышает 100 мкм, что дает возможность использования подобных устройств для измерения размеров трехмерных объектов в оперативных условиях (например, при фиксации ДТП или летучем контроле деталей на производстве).