Алгоритм обращения эрмитовой матрицы

3Academician A.L. Mints Radiotechnical Institute, JSC. Standalone division in Rostov-on-Don, Russian Federation

Введение. На современном этапе развития радиоэлектронных систем (РЭС) в области связи, радиолокации и радионавигации отмечается значительное усложнение электромагнитной обстановки. Это связано с высокой пространственной плотностью размещения РЭС и ограничениями используемых частотных диапазонов. Так, по данным [1], ЧИСЛО базовых станций формата 3G/4G только одного российского оператора «МегаФон» к концу 2013 года составляло порядка 43,5 тыс.

В данных условиях, как правило, параметры мешающих сигналов (в первую очередь, направление прихода), неизвестны. Поэтому для обеспечения помехоустойчивого приема применяются методы адаптивного формирования «нулей» диаграммы направленности (ДН) в многоканальной антенной системе — адаптивной антенной решетке (ААР) [2–4]. Функциональная схема получаемой при этом адаптивной антенны показана на рис. 1 [2].

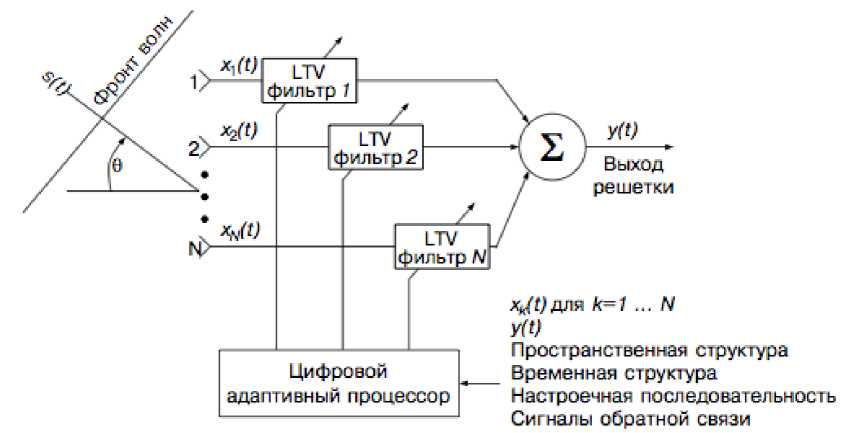
Рис. 1 . Функциональная схема антенны

Конструкция антенны (схема расположения излучающих элементов) выбирается в зависимости от требуемых характеристик. В общем случае схема включает многоэлементную антенную решетку, диаграммообразующую схему и цифровой адаптивный процессор. Антенная решетка используется для приема сигналов, которые суммируются с весовыми коэффициентами, вычисленными_адаптивным процессором в диаграммообразующей схеме для формирования диаграммы направленности антенны.

Обработка сигналов в адаптивном процессоре базируется на использовании современных методов спектрального анализа [2–4]. Они позволяют определять число и угловые координаты источников излучения, не прибегая к электрическому или механическому перемещению диаграммы направленности антенны. Используются исключительно алгоритмические способы обработки сигналов, принятых элементами антенной решетки. В результате можно в режиме реального времени отслеживать координаты источников излучения, находящихся в зоне наблюдения. В этом заключается основное достоинство методов спектрального анализа. Общая их особенность — использование взаимно-спектральной матрицы сигнала (ковариационной матрицы), оцениваемой на некоторой заданной частоте или в некоторой узкой полосе частот выходного сигнала приемника. С точки зрения теории, методы локализации источников излучения могут быть применимы только с некоторой задержкой, связанной с накоплением определенного числа мгновенных выборок (снимков) выходов приемников. Причем чем больше размер накопленных выборок, тем точнее получаются результаты.

Используемые в адаптивном процессоре алгоритмы базируются на нелинейной обработке сигналов методами линейной алгебры и теории матрицы с обращением или спектральным разложением корреляционной матрицы входных сигналов, имеющей большую размерность. Реализовать такую обработку в реальном масштабе времени в настоящее время затруднительно даже на самой современной элементной базе [5]. В связи с этим актуальной является задача поиска алгоритмов, упрощающих процесс обращения с учетом свойств матрицы, включая и алгоритмы получения решения в аналитической или полу аналитической форме [6, 7]. Так, в ряде работ, например [8–16], рассматриваются алгоритмы формирования обратной матрицы. В работе [1 7] описывается устройство, реализующее процесс получения обратной матрицы. Его построение основывается на использовании метода Гаусса — Жордана, представленного рекуррентными соотношениями. В работах [15, 16, 18] предложен алгоритм обращения, основанный на использовании метода окаймления [1 9]. Однако в указанных алгоритмах не учитываются свойства обращаемой матрицы.

Цель работы – повышение быстродействия устройства обращения ковариационной матрицы помех адаптивной антенной решетки путем сокращения числа выполняемых операций на основе использования в алгоритме обра-

Информатика, вычислительная техника и управление

щения априорной информации о свойствах эрмитовости матрицы.

Выявление свойств ковариационной матрицы. Для выявления свойств обращаемой ковариационной матрицы помех рассмотрим модель задачи определения направления прихода сигнала -

Математическое описание алгоритма определения направления прихода сигнала формулируется следующим образом [2-4, 8]. Пусть N-элементная антенная решетка с идеальной точностью принимает сигналы, передаваемые M рассеивающей, а источники излучения находятся в ее дальней зоне. Пусть канал системы передачи является узкополосным. Значит, по мере прохождения с направления 6m (m = 1,2 ... M) радиосигнала S(t)=[S1(t),S2(t),...,SM(t)]T через решетку в виде волновых фронтов его огибающая остается неизменной. Здесь Т — символ транспонирования. Предположим, что отклик решетки на каждый сигнал является функцией только одного углового параметра 6m . Требуется определить направление прихода волны 9m -

С учетом сделанных предположений пространственно -временная обработка сигнала разделяется на пространственную и временную, выполняемые в произвольном порядке. В результате суммарный измеряемый сигнал определяется выражением [2]:

x (t ) = A(0) S (t) + n (t), где n(t) = [n1(t),n2(t),----nM(t)]T — комплексный низкочастотный сигнал, эквивалентный полученному сигнальному вектору на антенной решетке в момент времени t; A(0) = [at^),af^),----#(ем)]T — вектор отклика решетки в направлении 9 m -

Известно большое число алгоритмов для обработки принятых антенными элементами данных с целью определения направления на источник излучения [2]- Так, для алгоритма «сверхразрешения», подробно описанного в [2, 4], направления прихода сигналов определяются положением пиков в пространственном распределении мощности:

Р= ( А ^Я (S) R Xx А(6)У^а

Здесь корреляционная матрица входных сигналов определяется выражением Rxx=A(0) R55A1 OV^ I, а функция ковариации входных сигналов определяется соотношением

R = R = lirn— Vx ( t„ ) X ^я ( t„ ), ⁵⁵ N Nt £f

где Nt — размер выборки; о² — дисперсия шума; I — единичная матрица; Я — символ эрмитового сопряжения.

– необходимо осуществить обращение ковариационной матрицы. Ее размерность а также точность получаемых результатов определяются размером выборки: чем больше объем выборки, тем более точные результаты могут быть получены. Обращаемая матрица, как несложно заметить из анализа выражения (4), обладает свойством эрмитовости [19].

Таким образом, при разработке алгоритма обращения корреляционной матрицы помех, имеющей большую размерность, необходимо учитывать ее эрмитовость-

Алгоритм обращения матрицы с учетом эрмитовости. Пусть эрмитовая матрица M порядка N является заданной и определяется следующим выражением:

	( s 5 11	5 12      -	-     5 1 N
M	5 21 ---	5 22     - ---       -	- 5 2 N -         -- -
	ч 5N 1	5N 2    -	-   5 nn /

-

B соответствии с предлагаемым алгоритмом на первом

шаге из элементов 5ij ( i = 1,

---,

N , j = 1,---, N ) матри-

ЦЫ M выбираются элементы ⁵ „ , s_n, ⁵ 21, ⁵ 22 ■ Данные элементы позволяют с формировать блочную матрицу M 2 ¹ "Л Я ЯМРГХТТСХРТТЛ ^ V ^ (Т)атПЩ1Л НЯ ЛРНЛ13Р ТТатаПТТУ ‘РКТНПР ТТОГР4ТР d ГТЯННТ-.ТР ^ттрЛ/ГРНТКТ    И1 ⁽¹⁾ Ш⁽¹⁾ Ш⁽¹⁾ Ш⁽¹⁾ Р ttUPTHM ^'ПК/ГТЛ"-^_/Ct.jlVlV> 1 xT ^ ^ . Mr L/^JlVl^y ЛпД £ld xJ xz 17txJ Dx/ IxxJ 1 xJ^_/.D.l.z\. DDt'ixlkzЛЛ-Гх./ 1 х/У1 ДиННЫС Д/ЛdV!^xl 1 Ы , 'i1 , 'm12 , m* 21 , m* 22 * J Л 1 x_tIVl jpiVllx товости матрицы M имеют вид:

⁵ 11 ⁵ 22

⁵ 22 ;

⁵ 11 ⁵ 22

I     ⁵ 12 ;

⁵ 11 ⁵ 22

I    ⁵ 21

⁵ 11 ⁵ 22

-1

*

(1)*

⁵ 12     m 2 ;

m

⁵ 11 5 22

I     ⁵ 11 -

На втором шаге происходит формирование обратной матрицы третьего порядка M ₃¹. Для построения данной

(2)      1

m 3 3 =H,

где Я = ⁵ 33 - ( ⁵ 31 ⁵ 32)

тЦ m ⁽ 2) т 211) т 22)

* T

( ⁵ 31 ⁵ 32)    .

матрицы дополнительно используются элементы 5 ,3, ⁵ 23, ⁵ 33, ⁵ 31, ⁵ 32 ковариационной матрицы M , окаймляющие полу.

ченную на первом шаге матрицу M 21, как приведено ниже: л т 1 ( 1) т™   5 13   . т 21) т 22)     5 23    . 5 31      5 32      5 33 .		5 ) .     5 1 N .    5 2 N .     5 3 N .	(7)
... 5 W 1 Однако для эрмитовой матрицы 5 13 =5 31*,	...        .. . ...      ... 5 N 2 5 N 3 ... 5 nn 7 * T-r 5 23 = 5 32 ■ Поэтому для нахождения матрицы третьего порядка до-

статочно использовать только элементы

5 31 , 5 32 , 5 33 ■ Элементы этой матрицы находятся с помощью формул:

Г m 1 < 1 2, т^ т 21) т 22) J

(т (1) т(1)          (') т(1)                                    (1) т(1) т 11 т 12       т 11 т 12           * T 1             т 11 т 12 5 5          5 5                ,                               (8) (1)    (1)            (1)    (1)        31 32               31 32         (1)    (1) ( )    ( )          ()()                                   ( )    ( ) 1 т 21 т 22 ) V т 21 т 22                           т 21 т 22 ) (2)              (1) ти(1) т 13          т 11 т 12           * T                                                        /03 5 5             , 31 32            , ( )                         ( )        ( ) т 23         т 21 т 22 (1)    М7(1) 1           т п т 12 т 5,) т(^         5 5              ,                                          (10) 31     32                    31 32         (1)    (1) х              H          т (/ т 22)

В общем случае для перехода от обратной матрицы Mn1 порядка n к обратной матрице Mn1 порядка n +1, выполняемого на n-м шаге преобразования, дополнительно используются приведенные на рис. 2:

— элементы { 5 1 _{n +}1, 5 _{2 n +}1,..., 5_{nn +}1 {, образующие матрицу-столбец B ;

— элементы { 5_{n +} 11, 5_{n +12},..., 5_{n +}1 _n {, обозначенные как матрица-строка C ;

^— элемент ⁵n ₊1 n , представляющий блок D .

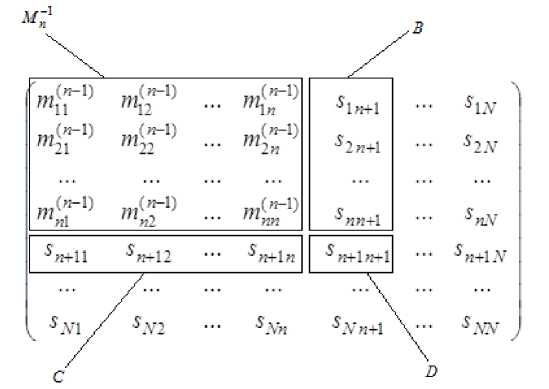
Рис. 2. Формирование структуры обращаемой матрицы

С учетом эрмитовых свойств матрица-столбец B равна комплексно сопряженной и транспонированной матрице -строке C, то есть B = C* T . Следовательно, матрица Mn 11, элементы которой определяются формулами, описан

Информатика, вычислительная техника и управление

ными в [ 19], примет вид:

_Mn 1₁

^M n ¹ +( H ¹ CM_n ¹)^{* T}CM_n ¹    ( H 1 _CMn 1 ₎ * T

-H ¹ CM ; 1             H 1

,

где H D CM_n ¹ C ^{* T} .

Оценка эффективности предложенного алгоритма. Для сравнения эффективности предложенного алгоритма обращения с известным алгоритмом на основе метода Гаусса — Жордана воспользуемся результатами работы [20]. Анализ соотношений, описывающих предложенный алгоритм обращения матрицы, показывает следующее. Для обращения матрицы R _xx размерности Nt X Nt с использованием метода Гаусса — Жордана потребуется ( Nt )³ операций умножения и сложения. При использовании предложенного метода окаймления с учетом свойств эрмитовости корреляционной матрицы R xx 0,75( Nt )³ + ( Nt )² операций. Таким образом, предложенный алгоритм обеспечивает для матриц больших размерностей, когда Nt —>оо , сокращение числа операций до (1 (0,75+1/ Nt )) 100 % 25 % .

Техническая реализация алгоритма. Схема устройства, реализующего предложенный алгоритм, отличается от устройства, описанного в работе [18] и основанного на использовании метода окаймления. При учете свойства эрмитовости обращаемой матрицы число вычислительных модулей может быть сокращено с 11 до 9, упрощается схемное выполнение вычислительных модулей, изменяются связи между ними. Кроме того, изготовление устройства обращения матрицы для реализации предложенного алгоритма не представляет особых затруднений, поскольку в операциях матричного умножения используются типовые цифровые блоки, выполняющие операции умножения, сложения и вычитания.

Блоки хранения коэффициентов матрицы могут быть выполнены на основе адресного запоминающего устройства, включающего блок памяти, дешифраторы и формирователи с регистром адреса, формирователи записи и усилители считывания с подключенным к ним регистром числа, а также блок синхронизации (управления).

Таким образом, устройство обращения ковариационной матрицы помеховых сигналов с учетом ее эрмитовых свойств позволяет за счет уменьшения числа вычислительных модулей упростить схему по сравнению с предложенной в [17]. Кроме того, с учетом сокращения требуемых для обращения операций можно повысить быстродействие работы устройства.

Заключение. В цифровых адаптивных процессорах радиоэлектронных средств при определении направления прихода сигнала широко применяются алгоритмы обращения корреляционной матрицы помеховых сигналов на основе учета ее свойств. Это определяет актуальность разработки подобных алгоритмов. При большом количестве сигналов, обусловленном плотным размещением средств радиосвязи в городских условиях, известные алгоритмы не обеспечивают вычисление пеленга в реальном режиме времени. Отличием предложенного алгоритма обращения является учет эрмитовых свойств ковариационной матрицы помеховых сигналов, позволивший почти на 25 % сократить объем вычислений. В результате устройство, реализующее операцию обращения корреляционной матрицы помех в цифровом вычислительном процессоре, будет более компактным по сравнению с известными, а также обеспечит более высокую скорость вычисления пеленга сигнала.