Алгоритм обратного преобразования Лапласа для обработки сложных релаксационных зависимостей

При исследовании динамики различных физико-химических процессов часто возникает задача выделения из сложной временной зависимости экспоненциальных релаксационных компонент вида

M ( t ) = M 0 e - t/T ,              (1)

где t — время, M — регистрируемая экспериментально величина, а T — время релаксации системы. При параллельном протекании нескольких релаксационных процессов, что имеет место, например, в гетерогенных системах или в гомогенных средах при наличии нескольких механизмов релаксации, кинетическая кривая может быть представлена в виде суммы некоторого количества экспоненциальных кинетических компонент. В частности, измерения времён продольной и поперечной релаксации в ЯМР, а также определение коэффициентов самодиффузии методом ЯМР с импульсным градиентом магнитного поля часто приводят к зависимостям M ( t ), которые не описываются одним временем релаксации [1, 2]. Кроме того, экспериментальная зависимость M ( t ) всегда содержит шумовую составляющую E ( t ). В случае аддитивного шума, вносимого, например, системой регистрации, временная зависимость M ( t ) будет иметь вид [3]:

N

M ( t ) = ^g i e ^{- t/T i} + E ( t )         (2)

i =1

(где g i — относительный вклад i -й компоненты: g i = M i (0) / £ M i (0)).

Стандартной процедурой выделения экспоненциальных компонент из сложной релаксационной зависимости (2) является представление экспериментальных данных в полулогарифмических координатах In M (t) — t, выделение наиболее медленной компоненты, экстраполяция её в область коротких времён и вычитание из исходной кинетической кривой [1]. Последовательное повторение этой процедуры позволяет выделить две-три экспоненциальные компоненты, надежные результаты получаются обычно в том случае, когда времена релаксации экспоненциальных составляющих различаются не менее, чем на порядок величины.

Выделение экспоненциальных компонент вида exp( —t/T i ) из экспериментальной зависимости (2) является плохо обусловленной задачей, поскольку экспоненциальные функции с действительным аргументом не являются ортогональными (в отличие от функций с мнимым аргументом, используемых в гармоническом анализе [1]). Задача существенно усложняется наличием шума и тем, что число экспоненциальных компонент N в соотношении (2) заранее не известно и должно быть определено из полученной в эксперименте зависимости M ( t ). Даже при сравнительно больших отношениях сигнал / шум ( ~ 100) выбор между представлениями (2) с N = 2 или N = 3 становится неоднозначным. Использование статистических оценок для анализа линеаризованных зависимостей, описываемых соотношением (2), сопряжено с большим объёмом вычислений, но из-за наличия шума не гарантирует однозначного результата [1].

Альтернативным подходом к анализу кинетических зависимостей вида (2) является использование обратного преобразования Лапласа ( L ^{- 1} ). Применение L ^{- 1} к экспоненциальной функции (1) преобразует её в дельта-функцию вида 5 ( т — T ) [4], в силу линейности преобразования Лапласа применение L ^{- 1} к зависимости вида (2) должно давать спектр времён релаксации T i исследуемой системы:

L

- 1

nn

Е g i e - t/T i = Eg i 5 ( т — T i ) •

Одним из достоинств данного подхода является то, что выполнение операции L-1 не требует апри- орного задания числа релаксационных компонент n.

В данной работе реализован алгоритм обратного преобразования Лапласа, предназначенный для получения спектра времён релаксации из экспериментальных данных, представляющих собой дискретный ряд значений M ( t k ). Проведен анализ разрешающей способности предложенного алгоритма на модельных системах в зависимости от длины временного ряда, от соотношения времён в спектре релаксации и от уровня шума в анализируемых данных.

Алгоритм обратного преобразования Лапласа. При обработке экспериментальных данных анализируемая временная последовательность M ( t ) задана на ограниченном количестве дискретных точек t k , а параметры n , g i и T i искомой функции (2) априори не известны. Алгоритмом, пригодным для получения спектра времён релаксации T i из кинетической кривой M ( t k ), является алгоритм SVD (singular value decomposition) [5 -- 7], кратко описанный ниже. Уравнение (2) — это частный случай уравнения Фредгольма 1-го рода:

M ( t ) = |

F ( t ) e t/^T dT + E ( t ) .

Для численного анализа данных соотношение (2) удобно переписать в матричном виде:

M = KF + E, (3) где M ( t k ) — вектор значений кинетической кривой M ( t ) размерности n ( n — количество дискретных значений t k ), K — ядро преобразования, представляющее собой квадратную матрицу, элементы которой выражаются соотношением: K kj = exp( -t _k /T j ), k = 1 , ..., n , j = 1 , ..., n , F ( T j ) — вектор значений искомого спектра времён релаксации F ( t ) для n точек T j .

Уравнение (3) формально можно переписать следующим образом: F = K - 1 ( M — E ). Однако матрица K вырождена (детерминант K равен нулю), следовательно, для неё не существует обратной матрицы. Используя метод сингулярного разложения матрицы, можно представить матрицу K в виде: K = U Е V T , где U , V — ортогональные матрицы, Е — диагональная матрица, на диагонали которой в порядке убывания расположены сингулярные значения матрицы K и нули. В этом случае уравнение (3) можно переписать в виде: F = ( V Е - ¹ U T ) M , где Е - ¹ — диагональная матрица, на диагонали которой расположены n _s обратных величин от сингулярных значений и нули.

На основе описанного выше алгоритма на языке программирования С++ была разработана программа, которая выполняет обратное преобразование Лапласа функции, заданной в виде дискретного набора точек, полученных в эксперименте. Результатом работы программы является дискретный набор точек спектра времён релаксации F (Tj) для заданных значений Tj. Количество точек τj равно количеству полученных в эксперименте точек кинетической кривой, а их значения равномерно распределены на логарифмической шкале внутри диапазона значений ti: Tj = 10 т min+ j (т max-тmin)/n, [ Tmin ,Tmax ] C [ t min ,t max]. Для анализа работы программы использовались модельные функции вида (2), задаваемые дискретными наборами из 50 точек ti. Точки ti также равномерно располагались на логарифмической шкале: ti = 10tmin+i(tmaxtmmin)/n.

Применение обратного преобразования Лапласа к модельным функциям. Модельная кинетическая кривая, используемая для тестирования разработанного алгоритма L ^{- 1} , представляет собой сумму пяти релаксационных компонент:

M ( t ) = M of 1 e - / 0 , 001 + -2 e 15            15	- t/ 0 , 01 , Ap- + 15	t/ 0 , 1 +
+ ± e - t 1 + A e - 15        15	t/ 10 .	(4)

Данный тест предполагает отсутствие шума. На рис. 1 представлена кинетическая зависимость (4) и спектр времён релаксации, полученный в результате применения обратного преобразования Лапласа к этой модельной кривой. На рис. 1 видно, что в отсутствие шума преобразование L ^{- 1} надежно разрешает времена релаксации, отличающиеся на порядок, и точно воспроизводит весовые коэффициенты g i .

Выбранное количество точек n = 50, в которых заданы значения кинетической кривой M ( t k ), является разумной величиной для длины временного ряда, который может быть получен в реальном эксперименте. С точки зрения практического применения важным является вопрос о влиянии длины временного ряда n на вид спектра F ( T j ). Для исследования этого вопроса обратное преобразование Лапласа было применено к модельной кинетической кривой, представляющей собой сумму двух компонент с равными весовыми коэффициентами и временами релаксации, различающимися на порядок:

M ( t ) = M о • (0 , 5 e ^{- / 0} , ¹ + 0 , 5 e ^{- / 1} , ⁰ ) . (5)

Варьируемой в этом тесте величиной является длина временного ряда n — количество точек t i , в которых заданы значения M ( t ). Результаты, приведённые на рис. 2, показывают, что спектры с приемлемым разрешением могут быть получены даже в случае коротких временных рядов ( n « 10). Существенное (до 500) увеличение числа точек релаксационной зависимости не приводит к принципиальному улучшению спектра времён релаксации, тогда как в реальных экспериментах получение большого количества значений M ( t k ) часто оказывается затруднительным. Оптимальной длиной временного ряда представляется величина n = 50, поэтому в дальнейших тестах все модельные кинетические зависимости представлены 50 значениями.

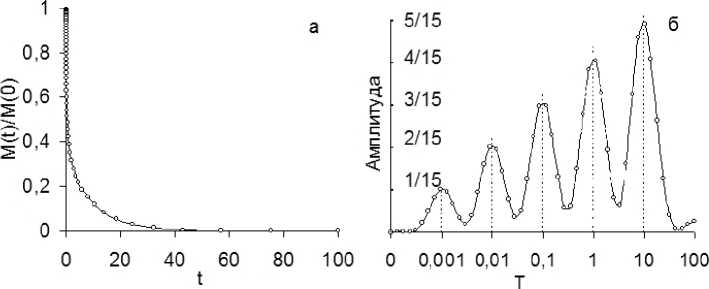
Рис. 1. а) Модельная кинетическая кривая, задаваемая соотношением (4), б) спектр времён релаксации, полученный путём применения обратного преобразования Лапласа к зависимости (4)

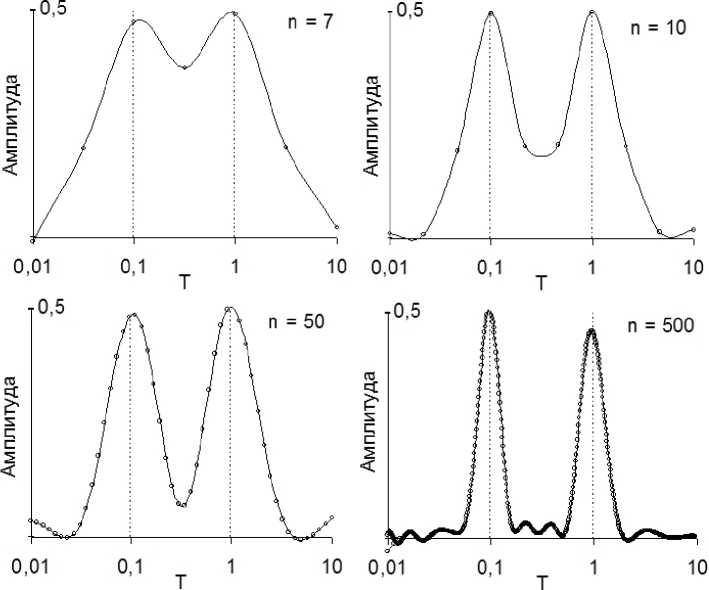
Рис. 2. Спектры времён релаксации, полученные для модельной кинетической кривой вида (5), при различной длине временного ряда n

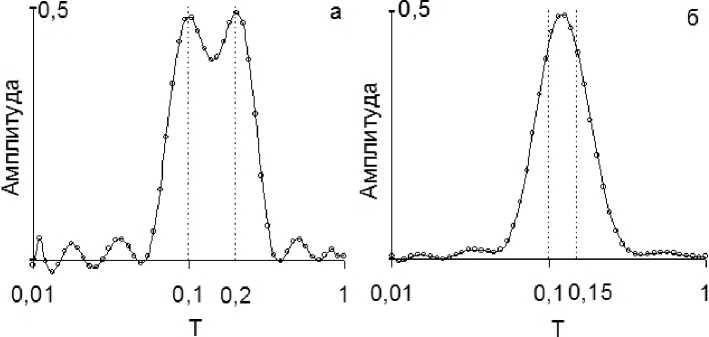
Рис. 3. Спектры времён релаксации, задаваемых соотношениями: M ( t ) = M ( t ) = M о • (0 , 5 e ^{-t/ 0} ' ¹ +0 , 5 e ^{-t/ 0} ' ¹⁵ ) (б)

полученные для модельных кривых,

M о • (0 , 5 e ^{-t/ 0} ' ¹ + 0 , 5 e ^{-t/ 0} ' 2 ) (а) и

При обработке экспериментальных данных ча- кинетические кривые вида (5), на которые был сто возникает необходимость выделения экспонен- наложен аддитивный шумовой сигнал. Аддитив-циальных компонент с близкими временами ре- ные шумовые сигналы достаточно часто встреча-лаксации. Стандартная процедура спрямления ки- ются в практике эксперимента, например, из-за нетической кривой в полулогарифмических коор- наличия собственных шумов системы регистра-динатах позволяет надежно определять времена ции [1]. Модельный шумовой сигнал представляет релаксации, различающиеся на десятичный по- собой белый шум, который моделировался набо-рядок величины [1, 2]. Для оценки разрешаю- ром случайных чисел r i . Для получения случай-щей способности алгоритма L ¹ проанализиро- ных чисел r i в диапазоне [ — 2 15 , + 2 15 ] использова-ваны модельные двухкомпонентные релаксацион- лась стандартная функция языка С++. Количе-ные кривые с близкими временами релаксации. ство случайных чисел выбиралось равным количе-На рис. 3 представлены результаты обработки мо- ству дискретных значений t _i анализируемой кине-дельных кривых, в которых времена релаксации тической кривой. Набор случайных чисел норми-компонентов различаются в два и полтора раза. ровался таким образом, чтобы отношение макси-Приведённые результаты позволяют заключить, мального случайного числа к значению M ( t 0 ) рав-что минимальное отношение времён релаксации, нялось заданному значению отношения сигнал / при котором они могут быть различимы в спектре шум ( SN R ). К каждому значению анализируемой L - 1 [ M ( t )] в отсутствие шума, равно двум. модельной релаксационной кривой M ( t i ) добавля-

Для оценки влияния шума на разрешающую лось число из набора r i . Типичный вид модель-способность предложенного алгоритма обратного ных релаксационных кривых с различным уров-преобразования Лапласа исследованы модельные нем шума приведён на рис. 4.

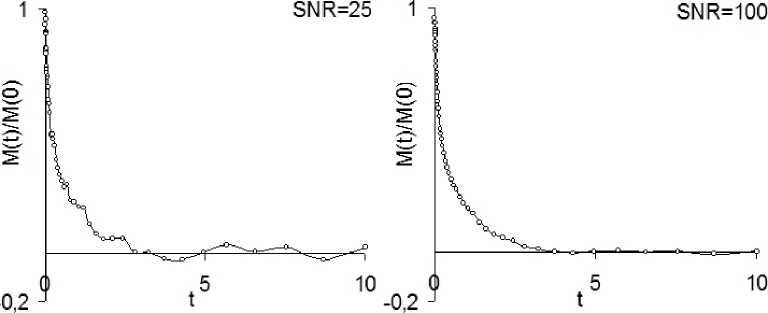
Рис. 4. Вид модельных релаксационных кривых типа (5) при различном уровне шума

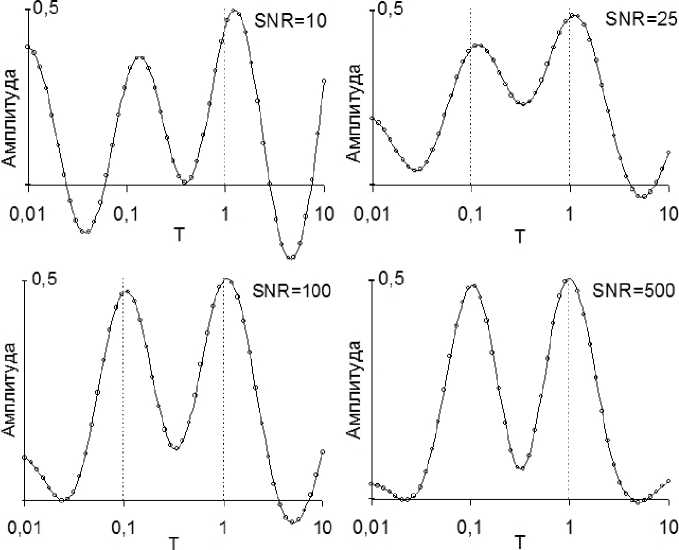
Рис. 5. Спектры времён релаксации, полученные для модельной кинетической кривой вида (5) при различном уровне шума

Влияние шума на спектр времён релаксации двухкомпонентной модельной кинетической кривой, получаемой с помощью преобразования L - 1 [ M ( t )], при различном отношении сигнал / шум иллюстрирует рис. 5. Результаты, приведённые на рис. 5, показывают, что отношение сигнал / шум 100 и более гарантирует точное воспроизведение функции M ( t ). При низких значениях SNR в спектре времён релаксации имеет место смещение максимумов и искажение соотношения весовых коэффициентов g i (около 20% при SNR = 10). Возрастание функции F ( T j ) на границах получаемого спектра времён релаксации (рис. 5) является артефактом, обусловленным конечной длиной анализируемого временного ряда. Уменьшение относительного вклада шумовой составляющей позволяет снизить влияние конечной длины временного ряда на вид спектра.

Обработка экспериментальных данных. Для оценки эффективности реализованного алго- ритма L-1 применительно к обработке реальных экспериментальных данных использованы результаты измерения времён продольной и поперечной релаксаций (T1 и T2) ядер лития 7Li методами ЯМР при различных температурах. Исследуемая система представляла собой ионообменную перфторированную мембрану МФ-4СК, применяемую в водородных топливных элементах, которая была переведена в Li+-форму. Полученные в экспериментах релаксационные данные представляют собой дискретный набор из 32 значений M (ti). Соотношение сигнал / шум для экспериментальных данных составляет в среднем 40. На рис. 6 приведён пример релаксационной кривой, зарегистрированной при температуре 283 К, а также спектр времён релаксации, полученный в результате применения преобразования L-1 к данной релаксационной зависимости.

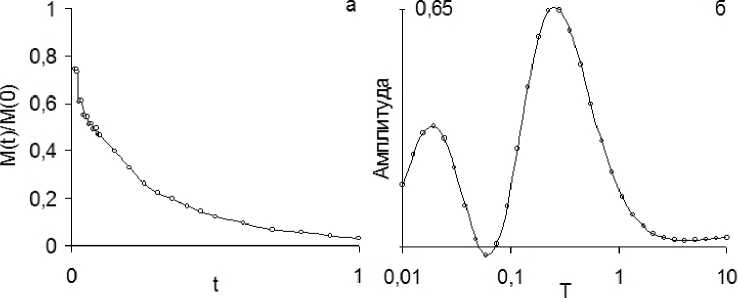
Рис. 6. Экспериментальная зависимость, полученная при измерении времени поперечной релаксации Т 2 для ядер 7 Li (а), и спектр времён релаксации, полученный из релаксационных данных с помощью обратного преобразования Лапласа (б)

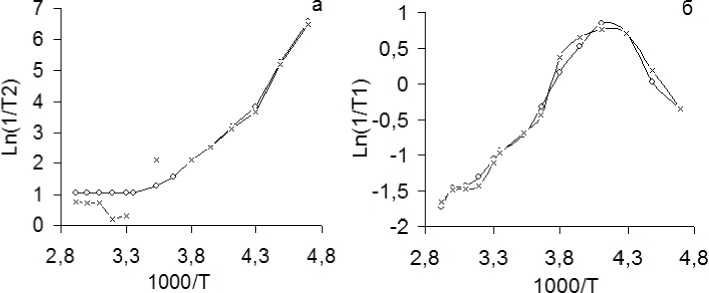
Рис. 7. Температурная зависимость скоростей релаксации 1 /Т ₂ (а) и 1 /Т 1 (б) для ядер 7 Li в ионообменной мембране: Q — результаты применения обратного преобразования Лапласа, х — результаты обработки стандартным методом

Экспериментальные релаксационные кривые, полученные при различных температурах, были обработаны двумя методами — стандартным методом (последовательным вычитанием экспоненциальных компонент из исходной кинетической кривой [8]) и методом обратного преобразования Лапласа. Анализируемые релаксационные кривые (рис. 6) представляют собой сумму двух кинети- ческих компонент, разрешение которых при высокой температуре стандартным методом затруднено вследствие высокого уровня шума. Температурные зависимости медленных компонент продольной (T1 ) и поперечной (T2) релаксаций в аррени-усовских координатах приведены на рис. 7. Сравнение двух методов обработки данных показывает, что стандартный метод спрямления в лога- рифмических координатах и обратное преобразование Лапласа дают практически одинаковые результаты (рис. 7б). Однако при наличии особенностей на исследуемых зависимостях использование обратного преобразования Лапласа демонстрирует некоторые преимущества. Например, применение L1 позволяет более надежно определить характер температурной зависимости скорости поперечной релаксации (1 /Т2) ядер Li в области 1000/Т м 3,3 (рис. 7а). Недостаточно критическое отношение к данным, получаемым стандартным методом обработки, может привести к выводу о наличии скачка скорости релаксации 1 /Т2 при 1000/Т м 3,3, что не соответствует действительности.

Таким образом, показано, что применение обратного преобразования Лапласа к релаксационным данным, включающим 50 дискретных значений, позволяет получать достоверные спектры времён релаксации в рутинных экспериментах. Надежное определение спектра времён релаксации достигается в том случае, когда временной диапазон регистрации релаксационной зависимости включает минимальное и максимальное значения определяемых времён T i . Предлагаемый алгоритм обратного преобразования Лапласа позволяет в отсутствие шума надежно разрешать времена релаксации, различающиеся в два и более раз. Высокий уровень шума приводит к погрешностям в определении величин T i и весовых коэффициентов, указанные погрешности достигают 20% при отношении сигнал / шум ~ 10. При соотношении сигнал / шум более 100 наличие шума практически не оказывает влияния на вид спектра времён релаксации.