Результатом спроса на резинотехнические изделия стало создание крупных промышленных производств синтетического каучука, история которого насчитывает уже более 100 лет [1]. Несмотря на большой исторический опыт предприятия вынуждены постоянно реагировать на современные требования рынка и корректировать технологические аспекты производства. Синтетический каучук относится к классу высокомолекулярных соединений, распределение которых по молекулярной массе определяет его физико-химические и потребительские свойства [2].

Управление молекулярной массой получаемого продукта производится добавлением реагентов [3‒5], выполняющих роль регулятора, в исходную реакционную смесь, которые принудительно вызывают обрыв и передачу цепи. Реакция передачи цепи используется для регулирования молекулярной массы полимера, получения 272

высокомолекулярных соединений с заданной молекулярной массой и полидисперсностью, а также для получения низкомолекулярных соединений.

Достаточно высокая реакционная способность регулятора приводит к его быстрому расходу и, как следствие, значительному повышению молекулярной массы продукта. Одним из путей решения является использование многоточечной подачи реагентов в технологический процесс.

В условиях действующего промышленного производства экспериментальным путем оценить влияние, оказываемое в результате многоточечной подачи реагентов, практически невозможно. Все более актуальным в этом случае становится вопрос развития математических подходов и вычислительных методов, позволяющих с использованием инструментов модельного описания системы воспроизводить различные сценарии с целью оценки влияния параметров исходной реакционной смеси и технологических аспектов непрерывного производства на физико-химические свойства продукта.

Целью данной работы является создание методологии, позволяющей с использованием инструментов модельного описания системы осуществлять направленное регулирование и построение технологического процесса для достижения заданного молекулярно-массового распределения.

Обзор литературы

Современные тенденции исследования новых и действующих промышленных процессов все чаще направлены на применение модельного подхода, позволяющего путем построения математической модели и проведения вычислительных экспериментов прогнозировать свойства продукта для различных исходных данных. Методы моделирования, применимые к процессам, лежащим в основе синтеза полимеров, направлены на решение задач поиска усредненных молекулярно-массовых и вязкостных показателей образующегося полимера [6; 7]. Математическое описание исследуемого процесса при этом базируется на представлении кинетического механизма [8] ведения элементарных реакций.

Математическое моделирование процессов синтеза полимеров предполагает применение двух подходов: кинетического [9] и статистического [10; 11]. В рамках реализации кинетического подхода предлагается формирование системы обыкновенных дифференциальных уравнений, характеризующих изменение материального баланса по каждому компоненту реакции и численное ее решение. В силу достаточно высокой размерности образуемой системы дифференциальных уравнений (порядка 106) применятся переход к усредненным молекулярным характеристикам с использованием статистических моментов молекулярномассового распределения [12].

Основы моделирования процессов полимеризации и расчеты кинетических схем подробно представлены в работах отечественных ученых [8; 9; 13‒15]. В зависимости от числа используемых мономеров и особенностей реализации процесса предлагается применять метод моментов [12] или метод производящих функций [16; 17].

В рамках описания крупнотоннажного производства предлагается модульный принцип построения модели, в соответствии с которым модель кинетики дополняется соответствующими гидродинамическими закономерностями, вид которых зависит от типа реакторов и системы организации непрерывного процесса [18]. Особенности моделирования процессов, протекающих в реакторах различных типов, а также изменение природы смешения реакционной смеси описаны в работах Р. Ариса, А. А. Берлина, С. А. Вольфсона [19; 20]. В рамках реализации системного подхода вычислительные эксперименты по оценке характеристик продукта в пусковом режиме непрерывного производства были проведены ранее для процесса полимеризации изопрена на неодимсодержащих каталитических системах с модифицирующими присадками TEA или TGA [21] и на титансодержащей каталитической системе [22]. К недостаткам реализации кинетического подхода в большинстве случаев относят ориентацию на расчет только усредненных молекулярных характеристик, а распределение образуемых макромолекул в таком случае воспроизводят с применением модельных функций в условиях принятия ряда допущений, что не всегда применимо к процессам промышленного производства полимеров.

Статистический подход (метод Монте-Карло) основан на вероятностной природе протекания реакций и учете каждой реакции как случайного события, вероятность которой зависит от различных факторов. Для реализации данного подхода наиболее удачно применим алгоритм Д. Гиллеспи [23]. В сравнении с кинетическим подходом проведение расчетов по статистическому подходу занимает гораздо большее время, однако позволяет детально подойти к вопросу исследования молекулярной структуры образуемого продукта. Основной проблемой реализации статистического подхода является низкая скорость расчетов, которая вынуждает использовать для расчетов малый объем ансамбля макромолекул и оптимизировать создаваемые алгоритмы под технологии параллельных вычислений.

Модификация математического описания под непрерывный режим производства требует введения стохастических величин, которые определяют вероятность нахождения макромолекулы в том или ином реакторе каскада. В этом случае стоит говорить о некотором среднем времени пребывания как о случайной величине, которая характеризуется вероятностной функцией распределения [24; 25].

Применение метода Монте-Карло к моделированию процессов полимеризации представлено в работах отечественных и зарубежных исследователей [26‒30]. В частности, представлены алгоритмы моделирования процесса катионной сополимеризации изобутилена с изопреном [31], процесса полимеризации изопрена в присутствии каталитической системы TiCl4– tBuCl с применением инверсного алгоритма [32].

С целью снижения временных затрат на организацию вычислений отдельно стоит выделить метод, основанный на идее воспроизведения цепи полимера из небольших фрагментов (блоков связей) [33; 34], концентрация которых может быть получена путем применения кинетического подхода. Под блоком связей понимается некая совокупность связанных между собой звеньев. В работе [35] концепция блоков связей использована для анализа кинетики сополи-конденсации и структуры сополимеров. В работе [36] продемонстрирована возможность простого и адекватного прогнозирования топологической структуры модифицированных эпоксиаминных матриц, основанная на концепции блоков 274

связей, сочетающей в себе кинетический и статистический подходы. В работе [37] концепция блоков связей была модифицирована и предложен алгоритм для процессов радикальной полимеризации.

Материалы и методы

Опишем основные этапы комплексного подхода, определяющие основу создания алгоритмов решения задач эмпирической оценки свойств продукта для различных режимов регулирования.

Этап 1. Кинетический механизм, определяет основные элементарные реакции, приводящие к образованию высокомолекулярных соединений. Данный шаг необходим для модельного описания в рамках реализации как кинетического, так и статистического подхода.

Для процессов гомополимеризации характерно наличие лишь одного вида мономера M , а кинетическая схема включает в себя стадии роста цепи, передачи цепи на мономер, на алюминийоргани-ческое соединение (регулятор) и гибели активных центров

P + M      >  P^ ,, P + M km >  Q + P ,

I                                  I +1■             I                                    I 1■

P + A■ >Qi+ P^ P     ,Qi, где M – концентрация мономера; A – концентрация АОС; Pi – активная («растущая») цепь полимера длиной i; Qi – неактивная («мертвая») цепь полимера длиной i; kp, km, ka, kd – константы, характеризующие скорость реакции роста цепи, передачи на мономер, на алюми-нийорганическое соединение и гибели активных центров соответственно.

Для процессов сополимеризации характерно наличие двух видов мономеров M ¹ и M ² . Как следствие, кинетический механизм процесса усложняется и характеризуется четырьмя типами реакций роста и обрыва цепей:

pi ₊ m¹ — kip > P^x n , m ^{+               77} n +1, m ,

i i            kpP

• ¹    n, m ^{+                 71} n, m +1 ,

• p. ₊ pj ^^ Q   ,

n,m      r,q ..       n^n+r,m+q , i            j       kdj

• ¹    n, m ^ ¹ r, q        ^{T Q}n, m ^ Q r , q ,

  где P_{n , m} , Q_{n , m} – активная и неактивная цепь сополимера длиной n + m , содержащая n звеньев мономера бутадиена и m звеньев стирола, i характеризует тип мономера на конце растущей цепи.

  Доминирующую роль в обрыве цепочек макромолекул выполняет стадия взаимодействия с молекулами регулятора S

  P nim m + S ' -^ Q n , „ + R .

  Этап 2. Построение математической модели в рамках реализации кинетического подхода подразумевает формирование соответствующей модели в виде системы обыкновенных дифференциальных уравнений, характеризующих изменение материального баланса по каждому компоненту реакций. Размерность полученной системы пропорциональна длине образуемых макромолекул, которая может доходить до 10 6 . Анализ характеристик получаемого продукта в этом случае предполагает использование моментов активных μ j и неактивных цепей η j [12] j -го порядка, которые для процессов гомополимеризации примут вид:

  +to +^

  Н^'Р , т , =^й. (1) i = 2 i = 2

  Полученные значения необходимы для расчета среднечисленной M_n и среднемассовой M_w молекулярной массы:

  
  

  На основании полученных значений можно будет идентифицировать усредненные молекулярные массы продукта

  
  

  ^Q M n

  
  

  ^Q M w

  
  

  _ V M ¹ + V M ² + v 1 V M ^{1 +} V M ^{2 +} V 0 ,

  _ V M ⁺ V M^{2 +} V 2

  
  

  V M ^{1 +} V i M 2 ⁺ v 1

  
  

  .

  
  
  
  

  Этап 3. Адаптация модельного описания под масштаб производства подразумевает учет соответствующих гидродинамических закономерностей, различающихся от типа реактора. В условиях отечественного промышленного производства непрерывный процесс реализуется в каскаде реакторов идеального перемешивания непрерывного действия. Учитывая высокую скорость перемешивания, можно считать, что в любой момент времени отсутствуют градиенты температуры и концентраций реагентов в реакторе. Моменты молекулярно-массового распределения в этом случае можно выразить через рекуррентные соотношения [8]:

  
  

  Y ( k - 1) _ y ( k )

  
  

  0 ^{( k} )

  
  

  + R y^k )

  
  

  = 0,

  
  
  
  

  M n

  
  

  = m о

  
  

  Ц 1 ⁺ Ц Ц о ⁺ Ц о ,

  
  

  ^M w = m 0

  
  

  ^Ц 2 ^{+ Ц} 2

  Ц ⁺ Ц

  
  

  , (2)

  
  

  где m₀ – молекулярная масса исходного мономера.

  Выражения для статистических моментов для процессов сополимеризации будут зависеть от молярной массы мономеров первого и второго типа M_a , M_b :

  
  

  V M ’

  
  

  ^ M ²

  
  

  — X — X

  = ЕЕ ( nM a + mM b ) Xm. ,

  n = 0 m = 0

  -x -x

  = EE ( nM a + mM b ) X m ,

  n = 0 m = 0

  -x -x

  
  

  X = EE ⁽ n^M a ^- m^M ) " б -n =0 m =0

  
  
  
  

  где 0 ( ^k ) - время нахождения реакционной смеси в к -том реакторе каскада; вид R ^^k ) определяется принятым кинетическим модулем, а вектор Y - размерностью исходной системы уравнений . Использование (6) для модельного описания позволяет выявить закономерности изменения характеристик [38] в статических режимах производства, для которых характерно отсутствие изменений концентраций исходных веществ в пределах одного реактора.

  В частности, для представленной выше кинетической схемы процесса сополимеризации модельное описание примет вид системы нелинейных алгебраических уравнений, решаемых с использованием классических численных методов:

  
  

  I ' k - 1)

  
  

  —

  
  

  0 ' ^k )

  
  

  T ' k ) --*i ' ^k ) = 0,

  
  

  M ¹ ' ^{k —1})

  
  

  —

  
  

  M 1' ^k )

  
  

  0 ' ^k )

  
  

+ro +ro

— kp 11M *'k) ZZ P^m n=0 m=0

—

+Ю +Ю

— k p 21 M *' k ) ZZ P .mk ) = 0, n = 0 m = 0

M ²' ^{k —}1)

—

M ²' ^k )

0 ' ^k )

+o> +ro

— kp 12 M2'k) ZE P^m n=0 m=0

+x +x

— k p 22 m 2'^k ) zz P 2 m^k ) = 0, n = 0 m = 0

5 ' ^{k —}1)

—

5 ' ^k )

0 ' ^k )

+ro +o>

T ' k) W PKk reg 1   ZZ^ n, m n=0 m=0

—

+Ю +to

— k reg 2 5 ' ^k ) ZE P 2 m^k ) = 0, n = 0 m = 0

v Q ' ^k " ¹⁾

—

0 ' ^k )

v Q ' ^k )    ( 1

¹-------⁺ l 2 k r 11 ⁺ k d 11

—

I +

+ ( k r 12 + 2 k ,,2 ) v M*‘ v M‘"' +

(1,

+ k

( 2

- d 22

1 ²₊ t    S' k )    M 1* k )

I ■ k reg 1 ^{5   v} 0

■ k reg 2 5 ' ^k v M ²' k ) = 0,

^ EE

—

w Q ' ^k )

^ 1___ ₊ (k  ₊k MM/^M '' ^k V M '' ^k )

_।        ⁺ ( t^r 11 ⁺ ^ d 11 ) ^v 0 ^v 1

+

0 ' ^k )

' k )    M 1' k )             ' k )    M ²' k)

■ k reg 1 ^{5   v} 1      ⁺ k reg 2 ^{5   v} 1

+

v M 1' ^k ) v M ²' ^k ) + v M *k^k v M ²' ^k ) )

+

+ (kr 22 + kd 22 )v M2( k )vM2( k) = 0, v Q'k"1)

—

W Q ' ^k )

^- ■ ( k r 11 ■ k d 11 ) v M’“ v M' ‘ ) ■

0 ' ^k )

' k )    M 1' k )             ' k ) M ²' k )

■ k reg 1 ^{5   v} 2     ⁺ k reg 2 ^{5   v} 2     ⁺

+

v M -( k v M ²' ^k) + v M ^{1( k} v M ²' ^k )

+ ( k r 22 + k d 22 ) v M ²⁽ k) V M ²⁽ k) +

+ k r 11 ( v M^{4 k}) ) ² + 2 k r v oM⁴ k ^ M ^{2( k}) +

■ k r 22 ( Г ^' * ' ) ’

С начальными условиями:

I (°’(0) = 1 ₀, M ¹<⁰⁾(Q) = M 1 ,

M ^2(Q)(0) = M 0 , S ⁽⁰⁾(Q) = S ₀,

^ Q ⁽⁰⁾(0) = V M ^{1 (0)}(0) =

= V M ^{2 (0)}(0) = 0, i = 0,1,2.      (8)

Этап 4. Реализация статистического подхода [39] к моделированию процесса подразумевает постоянную фиксацию в динамической памяти компьютера всех переменных, определяющих структуру и молекулярную цепочку каждой из макромолекул. Объем моделируемого ансамбля, определяющего реакционный объем, влияет на скорость моделирования и точность получаемых расчетных результатов, однако его задаваемая величина должна гарантировать получение устойчивых результатов в условиях многочисленных вычислительных экспериментов.

После формального описания кинетического механизма необходимо определить весь реакционный объем, который позволит рассчитать скорость осуществления каждой реакции в соответствии с выражением R i = k_tX A X B , где k i - константа, характеризующая скорость реакции под номером i , в которой принимают участие реагенты A и B ; X_A, X_B – молекулярная концентрация этих реагентов. Полученные значения в свою очередь используются для определения вероятности осуществления каждой реакции p i = R i / ( R 1 + R 2 + ... + R_n ) , а генерация случайных чисел, равномерно распределенных на отрезке [0;1], позволяет сделать выбор реакции и ее имитационное исполнение, под которым подразумевается набор действий, происходящих в этот момент в системе: уменьшение количества молекул одного реагента и увеличение молекулярной концентрации другого. Для выбора и исполнения очередной реакции требуется пересчитать все вероятности, поскольку концентрация реагентов каждый раз меняется.

Для процессов сополимеризации реализация алгоритмов не будет иметь конструктивные отличия кроме увеличения количества используемых динамических переменных для осуществления расчетов и добавления еще одной размерности, отвечающей за номер типа присоединяемого мономера.

Этап 5. Адаптация статистического подхода под крупнотоннажный режим производства требует введения параметра, характеризующего вероятность пребывания макромолекулы в том или ином реакторе каскада. При достижении порогового значения времени осуществляется программный перевод макромолекулы и расчет нового времени пребывания в соответствии с распределением:

Р п ^{( т} ) =

( " - 1)!

т" ¹

-т / е e

,

где 0 - среднее время нахождения реакционной смеси в реакторе каскада; τ – вероятностное время пребывания в реакторе; n – количество реакторов каскада. Поскольку начальные условия ведения процесса определяют массовую нагрузку и количество реакторов каскада, то в зависимости от объема реактора V время пребывания реакционной массы в нем может быть разным и определяется исходя из отношения 0 = V / C f ( C f - объемная скорость потока).

Чаще всего реализация статистического подхода необходима для оценки распределения получаемого продукта по массе и составу образуемых макромолекул. Применительно к процессам сополимеризации интересен анализ структуры молекулярных звеньев продукта [40], определяющий долю различного типа гомодиад в общем составе.

Этап 6. Воспроизведение молекулярно-массового распределения в рамках реализации статистического подхода позволяет избежать применения модельных функций и использования допущений при математическом описании процесса. Для оценки молекулярно-массового распределения продукта разработана методика, в основе которой лежит цифровая имитация процедуры фракционирования макромолекул полимера. Основная ее идея заключается в том, что в результате моделирования элементарных реакций происходит формирование массивов активных P[i] и неактивных Q[i] макромолекул, анализ которых позволяет проводить одновременный расчет и фиксацию молекулярной массы massQ[i] каждой такой макромолекулы. Для этого численно разбиваем данные значения на группы (или фракции) fract[i] с заданным шагом фракционирования ∆W исходя из условий

0 <  ^ massQ[i ] < A W ^ fract [1] = i

= ^ massQ [ i ], i

A W <  ^ massQ [ i ] <  2 - A W ^ fract [2] = i

= ^ massQ [ i ], i

• 2    - A W <  ^ massQ[i ] <  3 - A W ^ fract [3] = i

= ^ massQ[ i ],... i

Для каждой образованной группы вычисляем сумму фракции и рассчитываем ее массовую долю fractW [ i ] = = fract [ i ]/ ^ fract [ i ].

Для окончательной обработки требуется произвести лишь нормализацию полученных значений, поделив ее на шаг фракционирования.

С целью математического описания механизма многоточечной подачи регулятора формируется множество R = = {r 1, r2, ... ,rN}, которое численно определяет объем очередной дозировки соответствующих примесей в каждый реактор каскада с номером k. Очевидно, что r1 + r2 + … + rN = [S], а начальные условия определяются исходя из S0 = r1. При решении системы нелинейных алгебраических уравнений для каждого k-го реактора каскада требуется увеличивать концентрацию регулятора на величину rk, т. е. [5]к = [5]k + rk.

Таким образом, представленная методология решения прямых задач позволяет на основе математических моделей химической кинетики осуществлять контроль качественных показателей получаемого продукта для различных исходных условий ведения процесса и технологических аспектов организации непрерывного производства. Обоснованный выбор подхода к исследованию процессов определяется масштабом проводимого исследования и поставленными задачами. Реализация основных этапов моделирования процесса определяет методологическое наполнение соответствующих алгоритмов решения задач эмпирической оценки и схематично представлена на рисунке 1.

Результаты исследования

Апробация созданной методологии осуществлялась на реальном производстве. Соотношение бутадиена со стиролом в мономерной фазе по массовым частям составляет 70:30. Для регулирования молекулярной массы применяется трет-додецичный меркаптан, многоточечная подача которого возможна в соответствии с аппаратурным оформлением производства (рис. 2). Массовое соотношение воды к мономерам составляет 220:100. Для прекращения роста конверсии в качестве стоппера применяется диэтилгидроксиламин, который аппаратно вводится в конечный полимеризатор батареи.

Методология решения / Solution methodology

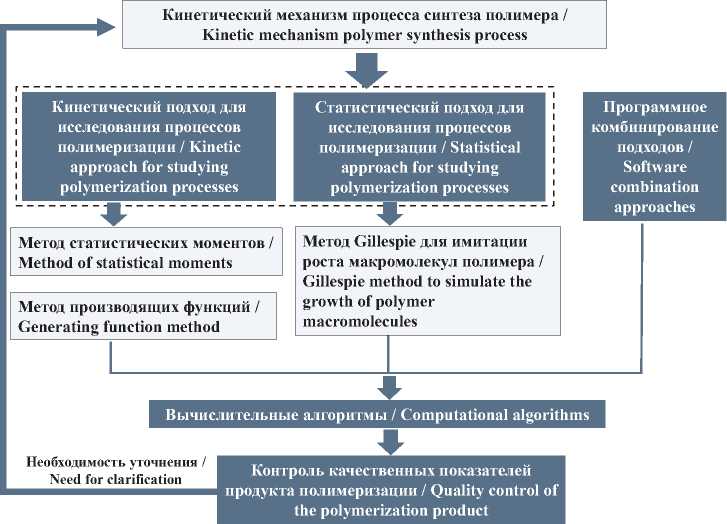
Р и с. 1. Методология решения задач исследования процессов синтеза полимеров

F i g. 1. Methodology for solving problems of process research polymer synthesis

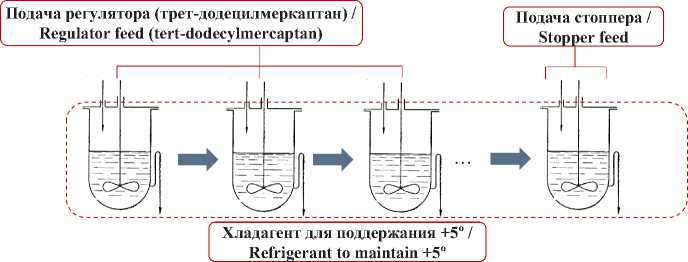
Р и с. 2. Схема непрерывного производства синтетического каучука путем эмульсионной сополимеризации бутадиена со стиролом

F i g. 2. Scheme of continuous production of synthetic rubber by emulsion copolymerization of butadiene with styrene

Механизм ведения процесса в условиях двухточечного регулирования предполагает использование 9 реакторов каскада при массовой нагрузке 2,75 т/ч, подача регулятора (трет-додецил меркаптана) осуществляется в две точки в соотношении 0,08 мас.ч. в 1 полимеризатор и 0,025 мас. ч. в 5 полимеризатор. В качестве инициатора процесса используется гидроперекись пинана с дозировкой 0,053 мас. ч. Для заданных условий регулирования исходный вектор R , определяющий механизм двухточечного регулирования, содержит следующие значения множества {0,08; 0; 0; 0; 0,025; 0; 0; 0; 0}.

В частности, для реализации статистического подхода к решению прямой задачи исходя из заданной концентрации реагентов был определен ансамбль макромолекул: бутадиен – 8,6·105, стирол – 1,9·105, инициатор – 200, регулятор (1 точка) – 260, регулятор (2 точка) – 80 молекул.

В условиях трехточечного регулирования потребуется 11 реакторов каскада при массовой нагрузке 3,5 т/ч по мономерам, регулятор (трет-додецил меркаптан) при этом подается в три точки в соотношении 0,125 мас. ч. в 1 полимеризатор и по 0,027 мас. ч. в 4 и 7 полимеризаторы. Для новых условий подачи регулятора исходный вектор R примет вид {0,125; 0; 0; 0,027; 0; 0; 0,027; 0; 0; 0; 0}.

Для оценки адекватности получае -мых расчетных результатов из каждого полимеризатора проводился отбор продукта в емкость со стоппером, который дегазировался от бутадиена, а получаемый в результате коагуляции каучук (сополимер) сушился и анализировался на такие показатели, как конверсия, массовое содержание мономеров и молекулярные характеристики в центральной заводской лаборатории предприятия ОАО «Синтез-Каучук» (Республика Баш-корстостан), предоставившего все необходимые экспериментальные данные. Результаты проведенных исследований для условий двухточечного регулирования производства приведены в таблице.

В рамках организации вычислительных экспериментов в соответствии с методологией, расчетным путем были получены зависимости конверсии и характеристической вязкости от номера полимеризатора (рис. 3, 4). При этом использовалась зависимость значений характеристической вязкости от значений среднемассовой молекулярной массы в соответствии с выражением Марка – Куна - Хаувинка, коэффициенты которого эмпирическим путем были определены в работе [41]:

. _ 1 85 [ Л ] = 5,4 - 10 4 M 0³⁶ ,М ^ = -,— M w . (10)

Т а б л и ц а

T a b l e

Результаты проведенных экспериментов The results of the experiments

Номер полимеризатора по ходу процесса / Number of the polymerizer during the process	Конверсия мономеров по сухому остатку латекса, % / Monomer conversion by latex dry residue, %	Характеристическая вязкость, [ η ] / Characteristic viscosity, [ η ]
2	27,0	0,86
3	–	1,28
4	42,0	1,94
5	–	1,77
6	63,0	2,13
7	—	2,16
9	73.3	2,57

Благодаря возможности имитации модельного времени, т. е. времени ведения эксперимента, можем наблюдать 2 серии кривых (после 15 и после 30 часов моделирования процесса). Очевидно, что 15 часов (штриховая линия) недостаточно для получения качественных расчетных результатов, в то время как 30 часов (сплошная линия) моделирования достаточно для стабилизации получаемых характеристик, которые можно рассматривать как значения, характерные для статических режимов непрерывного производства. Добавление второй порции регулятора в 5 полимеризатор приводит к снижению значений характеристической вязкости, конверсионная зависимость при этом не меняется.

Проведение вычислительного эксперимента для условий трехточечного регулирования позволило также добиться соответствия расчетных и экспериментальных данных. Вызывают интерес сравнение кривых, характеризующих распределение макромолекул по массе, полученные в рамках реализации

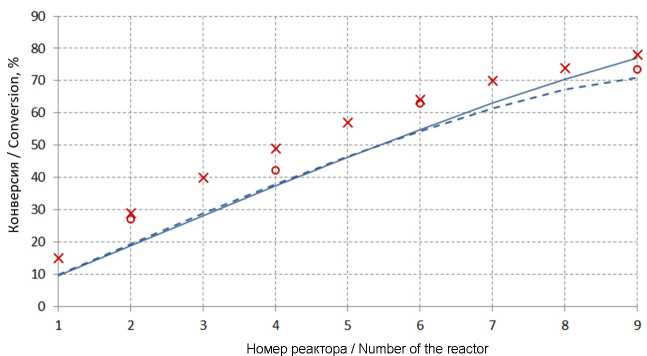
Р и с. 3. Изменение конверсии мономеров от номера полимеризатора (° - экспериментальные точки, х - результаты кинетического подхода; штриховая и сплошная линия – результаты статистического подхода после 15 и 30 часов ведения процесса)

F i g. 3. Change in the conversion of monomers from the polymerizer number

(° - experimental points, x - results of the kinetic approach; dashed and solid lines are the results of the statistical approach after 15 and 30 hours of the process)

280                                       Приборы и методы экспериментальной физики

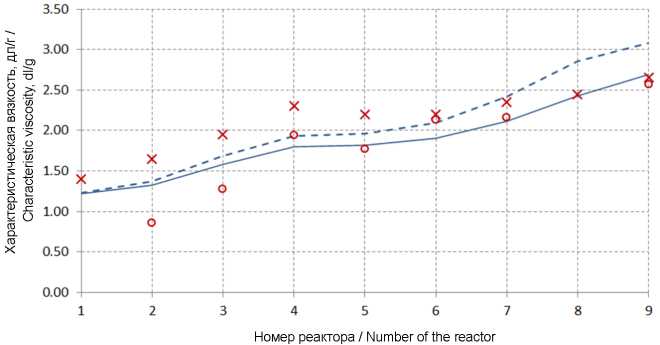
Р и с. 4. Изменение характеристической вязкости от номера полимеризатора

(º – экспериментальные точки; х – результаты кинетического подхода; штриховая и сплошная линия – результаты статистического подхода после 15 и 30 часов ведения процесса)

F i g. 4. Change in intrinsic viscosity versus polymerizer number

(° - experimental points; х - results of the kinetic approach; dashed and solid lines are the results of the statistical approach after 15 and 30 hours of the process)

статистического подхода согласно этапам 4-6. На рисунке 5 представлена визуализация дифференциальной кривой молекулярно-массового распределения для условий двухточечной и трехточечной подачи регулятора. Анализ кривых позволяет сделать вывод о том, что добавление третьей точки подачи регулятора способствует снижению среднемассовой молекулярной массы сополимера, при этом распределение характеризуется увеличением доли низкомолекулярных фракций и уменьшением доли высокомолекулярных фракций.

В проведенном анализе микроструктуры (рис. 6) наблюдается рост доли гомодиад бутадиен-бутадиен (BB) и соответствующее уменьшение доли гомодиад стирол-стирол (SS), что предопределяет снижение жесткости и соответственно увеличение показателей эластичности продукта.

Обсуждение и заключение

Представленная в работе методология исследования процессов синтеза полимеров позволяет на основе математических моделей химической кинетики осуществлять контроль физико-химических и потребительских параметров

Instruments and methods of experimental physics производимого продукта для различных исходных условий ведения процесса и технологических аспектов непрерывного производства. Программная реализация описанной методологии [42] и вычислительные эксперименты позволили решить задачу оценки влияния технологии многоточечного регулирования в промышленном производстве синтетического каучука.

В частности, для процесса сополимеризации бутадиена со стиролом вычислительные эксперименты позволили оценить влияние трехточечного регулирования молекулярной массы с применением тред-додецил меркаптана. Добавление третьей точки регулирования процесса позволило снизить значение среднемассовой молекулярной массы получаемого продукта, анализ молекулярно-массового распределения при этом показал увеличение доли низкомолекулярных фракций и уменьшение доли высокомолекулярных фракций.

Проведенный анализ структуры молекулярных звеньев в свою очередь характеризует снижение жесткости и увеличение эластичности получаемого продукта, а созданные инструменты 281

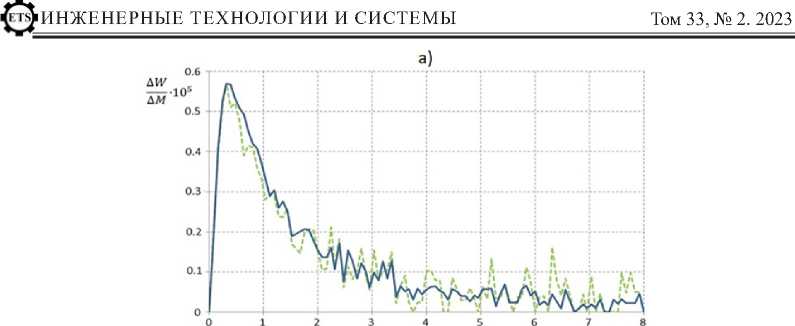
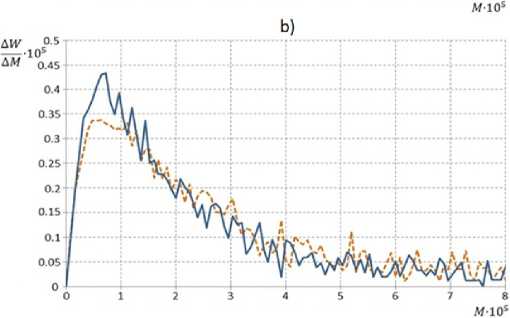
Р и с. 5. Дифференциальная кривая ММР для условий: а) двухточечного; b) трехточечного регулирования

F i g. 5. Differential MWD curve for conditions: a) two-point; b) three-point regulation

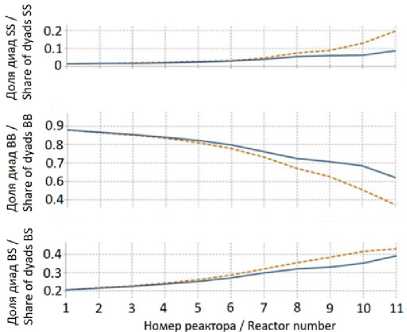
Р и с. 6. Зависимость значений доли гомодиад стирол-стирол (SS), бутадиен-бутадиен (BB), бутадиен-стирол (BS) в цепях сополимера от номера полимеризатора (пунктир –двухточечный режим, сплошная линия – трехточечный режим подачи регулятора)

F i g. 6. Dependence of the proportion of homodiads styrene-styrene (SS), butadiene-butadiene (BB), butadiene-styrene (BS) in the copolymer chains on the polymerizer number (dotted line – two-point mode, solid line – three-point mode of supply of the regulator)

оценки данного влияния позволяют путем организации многочисленных вычислительных экспериментов подбирать оптимальные параметры регулирования процессом промышленного синтеза полимерной продукции и решать перспективные задачи планирования производства.

Поступила 24.03.2023; одобрена после рецензирования 02.05.2023; принята к публикации 17.05.2023

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.

Submitted 24.03.2023; revised 02.05.2023; accepted 17.05.2023