Алгоритм оценки положения лазерного луча матричным фотоприемником на фоне гауссовского шума с использованием полной достаточной статистики принимаемого рассеянного излучения

Цитирование: Козирацкий, Ю. Л. Алгоритм оценки положения лазерного луча матричным фотоприемником на фоне гауссовского шума с использованием полной достаточной статистики принимаемого рассеянного излучения / Ю. Л. Козирацкий, Р. Г. Хильченко, Р. Е. Меркулов, А. А. Козирацкий // Журн. Сиб. федер. ун-та. Техника и технологии, 2021, 14(3). С. 265–271. DOI: 10.17516/1999–494X-0307

В математической статистике для отыскания эффективных оценок параметров распределений, обладающих полными достаточными статистиками, и функций от них успешно используется теорема Лемана-Шеффе [1–2]. На основе ее применения могут быть получены эффективные оценки параметров распределений и в тех случаях, когда наиболее эффективные оценки не существуют. К достоинству таких оценок следует отнести то, что они обеспечивают наилучшее качество оценивания параметров при любых конечных объемах выборки и не требуют дополнительных исследований. Указанная теорема может быть применена для решения задачи определения направления на источник лазерного излучения по проекции луча на приемной плоскости матричного фотопри-емного устройства (МФПУ), формируемой рассеивающей в атмосфере составляющей излучения.

Целью данной статьи является разработка алгоритма оценки положения лазерного луча по рассеянной в атмосфере составляющей матричным фотоприемным устройством на фоне гауссовского шума с использованием полной достаточной статистики.

Пусть в картинной плоскости МФПУ, представленной на рис. 1, наблюдается изображение проекции лазерного луча y ( x ), представляющее собой аддитивную смесь стационарного гауссова шума n( x ) с нулевым средним и дисперсией о², и полезного лазерного излучения S ( x ), изменяющегося по линейному закону S ( x ) = a • x + b .

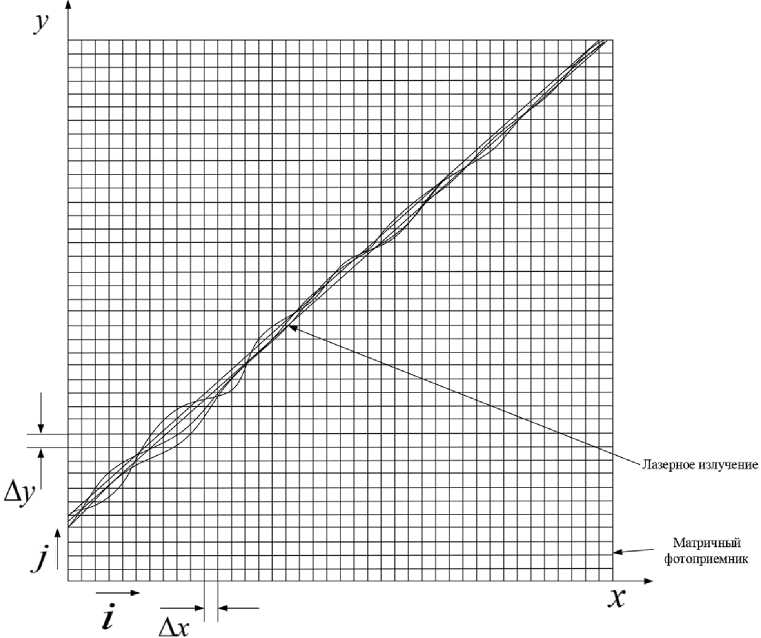
Рис. 1. Изображение проекции лазерного луча на картинной плоскости МФПУ

Fig. 1. Image of the laser beam projection on the MFP picture plane

Запишем выражение для принятой реализации смеси сигнала и шума:

y^ = 7](x) + S(x) = T](x) + a-x + b ,                                   (1)

где a – крутизна сигнала; b – постоянная составляющая.

Тогда неформализованная задача фильтрации входного сигнала (изображения) y ( х) от шумовой составляющей η( x ) сводится к определению эффективной оценки величин a и b и построению прямой S ( х ) в плоскости МФПУ.

Представим наблюдаемый процесс y ( х ) в виде вектора у = | 1у ,..., у у_п j, где yj = y ( xi) -отсчеты значений напряжения (тока); соответствующие максимальному количеству фотоэлектронов (квантов), зафиксированных в строке j и столбце i МФПУ (рис. 1); j = 1,..., n, i = 1,..., n, n – объем выборок (совпадает с числом элементов по строкам и столбцам матрицы размером n ^x n).

Представляя размеры элемента матрицы А х , А у интервалами дискретизации принятых отсчетов по строкам и столбцам, запишем выражение для единичного j -го отсчета:

у} = ^y • у = ту(/ • Ах) + а • г • Ах + b

Будем считать, что отсчеты yj статистически независимы, а дисперсия шума о² априорно неопределена.

Запишем совместную плотность распределения вероятностей вектора у:

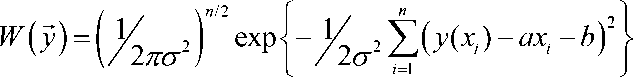
Преобразуем плотность распределения вероятностей к виду, удобному для обоснования алгоритма оценки указанных параметров:

^(y) = И'(Щу)) = С(С)ехр^1Н1 +g2H2+g3H,y

где (.т = ■_ig₁,g₂,g_?y — вектор параметров с компонентами g 1 = —1/2 а ², g ₂ = а / у ², g ₃ = b / у ²; ;                                           ;                                                 ;

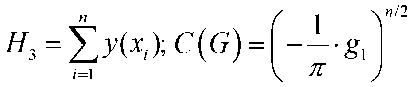
– нормирующий множитель.

Плотность распределения вероятностей принадлежит экспоненциальному семейству, вектор ее параметров G при неизвестных значениях а , b, а² принимает значения из области (–∞,0) × (–∞,∞) × (–∞,∞), т. е. содержит трехмерный интервал. Поскольку параметры a и b могут быть представлены в виде линейной комбинации моментов полной достаточной статистики H ( у ), то

L^jV^^        ^jZAx^j-l^^       ,  (5)

(Дх)'и(и + 1)(и-1)               Лх-и(и-1)

где

а^^хУ п^п + 1)(2л? + 1) й-«Ах(« + 1)

6         +     2

, z х z х а -и • Хх(п + 1А m\yG^ = M уН3} =--------- + п-Ь.

Используя методические рекомендации, изложенные в [3, 4], эффективную оценку параметров a и b можно найти в виде линейной комбинации соответствующих компонентов полной достаточной статистики:

_А Х1Н,-6Ьх(п^Х\Н₃ ; (zXx)" и(и + 1)(и -1)

а 2Аг(2л + 1)Я₃-6Я₂ Хх-п\п -\^

Выражая статистики H ₂ и H ₃ в (6) и (7) через компоненты вектора у и его исходных наблюдений, получаем

6^(2/-и-1)Х^)

;

Ах-я(и + 1)(/7-1) ²5L(2« + l-3/)X^) п^п -1)

Дисперсии оценок в этом случае могут быть определены с помощью выражений:

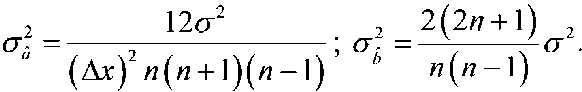
Применительно к матрице n × n для условий равенства Δ x = Δ y преобразуем полученные выражения к виду, удобному для построения структурной схемы обработки изображения, реализующей обоснованный алгоритм:

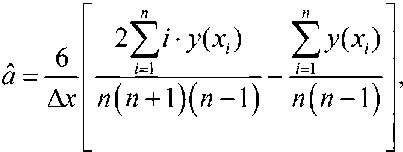
b =

4/7 + 2

п -n

'У/У^ ^.

/=1

Физический смысл входящих в выражения (11) и (12) величин поясняется на рис. 2.

При помощи среды моделирования MatLab Simulink представим выражения (11) и (12) в виде алгоритма оценки, на входе которого есть некая реализация принимаемого рассеянного лазерного излучения y ( x ) картинной плоскостью матричного фотоприемника, а на выходе – проекция полезного сигнала S ( x ) в виде линейной функции с параметрами и и b . Структура указанного алгоритма представлена на рис. 3.

Таким образом, на основе применения теоремы Лемана-Шеффе разработан алгоритм оценки положения лазерного луча в плоскости МФПУ. В качестве исследуемого процесса рассмотрена непрерывная реализация рассеянного в атмосфере лазерного излучения на фоне шума.

Указанная реализация достаточно обоснованно может быть представлена полной достаточной статистикой ее дискретных отсчетов, что является основным условием применения теоремы Лемана-Шеффе.

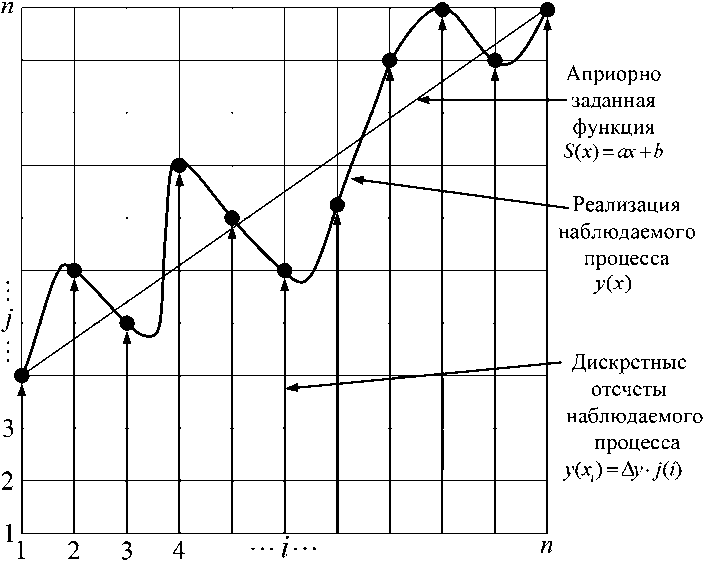
Рис. 2. Физический смысл величин, входящих в выражение оценки параметров а и b

Fig. 2. The physical meaning of the values included in the expression of the estimation of parameters и and b

– 269 –

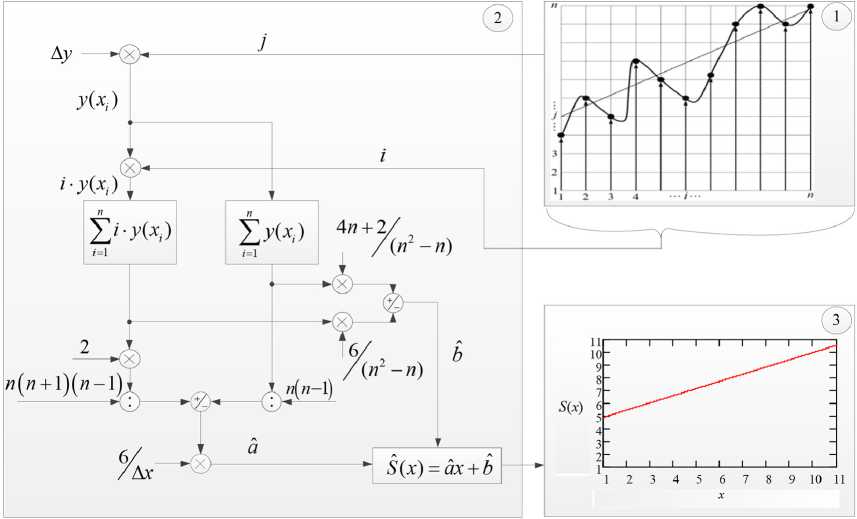
Рис. 3. Алгоритм оценки положения проекции лазерного луча

Fig. 3. Algorithm for estimating the position of the laser beam projection

На рис. 3 приняты следующие обозначения: 1 – реализация принимаемого рассеянного лазерного излучения y ( x ) картинной плоскостью МФПУ; 2 – алгоритм оценки положения лазерного луча; 3 – полученная проекция полезного сигнала S ( x ) в виде графика линейной функции с параметрами Cl и b .

Результатом работы алгоритма явились оценочные значения крутизны линейно изменяющейся функции полезного сигнала и постоянной составляющей этой функции. Подстановкой этих оценок в уравнение прямой происходит «восстановление» (избавление от шумовых флуктуаций) полезного сигнала. На рис. 3 с помощью графика (1) априорно заданного входного воздействия на приемную плоскость МФПУ после определения эффективных оценок Cl и b с помощью разработанного алгоритма получена проекция оси лазерного луча, которая идентична априорно заданной функции S ( x ).

Совместная обработка полученных оценок фотоприемниками в плоскостях, расположенных ортогонально относительно друг к другу [5, 6], позволяет оценить пространственное положение оптической оси лазерного луча в пространстве и определить направление на источник лазерного излучения.