Алгоритм определения координат земных станций по сигналам, спутников-ретрансляторов

В настоящее время отечественные комплексы радиомониторинга (КРМ), реализующие определение координат земных станций (ЗС) спутниковой связи по сигналам, принятым от спутников-ретрансляторов (СР) не эксплуатируются. Между тем нашли применение зарубежные КРМ, в ходе испытания которых были вскрыты следующие недостатки [1]: зависимость от производителя, закрытость системы, низкая оперативность, высокая стоимость, неэффективная топология КРМ.

Вышеуказанные    недостатки накладывают существенные ограничения на использование зарубежных КРМ, что стимулирует разработку отечественных аналогов. Наиболее сложным этапом является создание алгоритма определения координат ЗС по сигналам от СР.

Для наглядности алгоритма определения координат ЗС по сигналам, принятым от СР рассматривается геометрическая основа на плоскости, (рис. 1.), включающая КРМ R ( x_R , y_R ), ЗС N ( x_N , y_N ), 1-й СР А ( x 1 , у 1 ), 2-й СР В ( x ₂, у ₂). Также изображены: V 1 , V 2 - скорости 1-го и 2-го СР соответственно; 0 1 N - угол между V 1 и направлением на ЗС; 0 1 _R - угол между V 1 и направлением на КРМ; 0₂ N - угол между V 2 и направлением на ЗС; 0_{2 R} - угол между V 2 и направлением на КРМ; 0X и 0Y - оси координат.

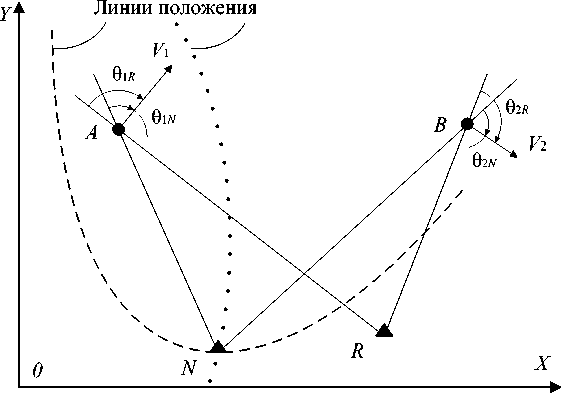
Рис. 1. Геометрическая основа алгоритма ОМП ЗС ССС

Зная координаты СР [2] и КРМ задача сводится к определению координат ЗС в наземном КРМ по сигналам, принятым от 1-го и 2-го СР, в ходе чего используется алгоритм, характерный для позиционных способов координатометрии.

Для построения линий положения возможно применить разностнодальномерный и (или) разностно-доплеровский способ [3, 4].

При разностно-дальномерном способе используется время задержки tЗ, вызванное разностью расстояний, прошедшим одним и тем же сигналом, излученным ЗС, через основной СР и зеркальный СР [5].

Возможно записать уравнение с двумя неизвестными x N , и y N :

7 (xi - xN )2 + (y - yN )2 + д/ (XR - x )2 + (yR - y )2 -

- V(x2 - xN )2 +(y2 - yN )2 - V(XR - x2 )2 +(yR - y2 )2 = ctЗ где c – скорость света.

Решением уравнения (1) будет гипербола с фокусами в точках A и B, показанная пунктиром (рис. 1).

В разностно-доплеровском способе используется доплеровское смещение частоты f D , вызванное движением СР относительно ЗС и КРМ. Частота сигнала, принимаемого КРМ от основного СР f 1 R равна:

f iR ^— f N ^{+ f} 1 D + f iG ⁺ f ID ,                       ⁽²⁾

где: fN - частота сигнала, излучаемого ЗС; f ^ -доплеровский сдвиг за счет сближения (удаления) СР и ЗС; f.G - частота "подставки" 1-го СР; f р - доплеровский сдвиг за счет сближения (удаления) СР и КРМ.

Можно получить выражение связывающее углы 9 1 N и 9 2 N :

_Л    ( У(Сc + V cos6₂ )) - ЬсЛс ² - V 2 )( С + V ²cos9₂ c ² - V ²) c

2R       2      2R     2G         2        2       2N1

COSUi n —                                       ..

(f1R (c + V1COS01R) - fG^c2 - V12)( c2 - V2)V1

Каждому значению 9 2 _N может соответствовать единственное значение 9 1 _N . Каждой паре 9 1 N и 9 2 N соответствует точка, принадлежащая линии положения, показанной штрихом (рис. 1).

При пересечении двух линий положения, полученных с помощью формул (1) и (3) получают координаты ЗС.

Для проверки адекватности разработанной модели было осуществлено имитационное моделирование на ЭВМ [6, 7]. Была произведена оценка точностных возможностей КРМ по определению координат ЗС с помощью раскрытого алгоритма [1].

Данная статья не закрывает рассматриваемую тему. Направлением дальнейших исследований может стать решение задачи, посвященной определению параметров движения ЗС [8] на основе разностнодоплеровских измерений различных реализаций одного и того же радиосигнала, принятого от нескольких СР.