Алгоритм оптимального адаптивного терминального управления расходом топлива жидкостной двигательной установки ракеты-носителя. Часть II

В данной статье на основании работ [1–10] для решения задачи оптимального адаптивного управления дискретной динамической системой предлагается рекуррентный алгоритм, который сводит исходную многошаговую задачу к решению конечной последовательности задач оптимального программного терминального управления в форме Задачи 1. В свою очередь, каждая Задача 1 сводится к реализации конечной последовательности одношаговых операций решения задач линейного и выпуклого математического программирования, алгебраических операций над выпуклыми компактными многогранниками, систем линейных алгебраических операций и вспомогательных одношаговых краевых задач для линейных управляемых систем.

Действие предлагаемых в работе алгоритмов реализовано в программной среде MATLAB и проиллюстрировано на модельном примере. Работа продолжает первую часть этой статьи, термины и обозначения из которой используются здесь без дополнительных пояснений.

1.    Алгоритм формирования множества оптимальных программныхтерминальных управлений

Пусть в дискретной динамической системе

x(t +1) = A(t)x(t) + B(t)и(t), x(0) = xо с ограничениями фазового состояния и управления

x(t) e X1(t) c R4, t e 0,T;(2)

и(t) e U1(t) c R1, t e 0, T -1,(3)

качество управления в которой на временном интервале т , T с 0, T оценивается функционалом

Л (w (т), и (•)) = | x (Т) - xd| |4 = Ф( x (T)),(4)

сформирована т-позиция w(e) (т) = {т, x(e) (т)} e W(t) (w(e)(0) = w0). Тогда для вычисления множества оптимальных программных управлений U(e) (т, T,{x(т)}, X(eL (T)) c и(т, T) разработан метод 'т, T прямых и обратных конструкций [3, 6], который применительно к рассматриваемой управляемой динамической системе реализуется путем выполнения нижеследующих операций:

• 1)    пошагового построения прямых областей достижимости G ₊ ( т , x ⁽ е ) ( т ); t ), V t eт + 1, T на основе модификации общего рекуррентного алгебраического метода [10] путем решения рекуррентной последовательности задач линейного математического программирования, выполнения одношаговых операций над компактными многогранниками и описания их с помощью вершин и конечных систем алгебраических равенств и неравенств;

• 2)    оптимизации функционала y ^ T ( w ( т ), и ( • )), определяемого (4), на множестве G ₊ ( т , x ⁽ e ) ( т ); T ), т. е. формирования множества X ⁽ e ) ( T ) c R ⁴ оптимальных финальных состояний системы (1)-(4)

^т, T путем решения следующей задачи выпуклого математического программирования [6, 11]:

X' (T) = |x(e) (T) I x(e) (T) e G+ (т,x(e) (т);T), 'т, T               I cYe)(т, T, w(т)) = Ф^ =       min       ||x(e) (T) - xd II |;

• ^т, T x ( T ) e G ₊ ( т , x ⁽ e ⁾( т ); T )^{H                    114}

• 3)    пошагового построения обратных областей достижимости G ( T , X ^{( e )} ( T ); t ),

⁷ т , T

V t e { T - 1, T - 2, „., т + 1} на основе модификации общего рекуррентного алгебраического метода [10] путем решения рекуррентной последовательности задач линейного математического программирования, выполнения одношаговых операций над компактными многогранниками и описания их с помощью вершин и конечных систем алгебраических равенств и неравенств;

• 4)    последовательного построения пересечений сформированных прямых и обратных областей достижимости путем реализации конечной последовательности одношаговых операций перехода от вершинного описания областей достижимости к описанию соответствующими системами линейных алгебраических уравнений и неравенств и наоборот:

G ( т , x ( т ); t ) = G₊ ( т , x ( т ); t ) П G ( T , X <1 ( T ); t ), V t e т , T - 1;

' т , T

G ( т , x ( т ); т ) = { x ( т )}; G ( т , x ( т ); T ) = X <1 ( T );

' т , T

• 5)    решения вспомогательных краевых задач на промежутке времени т, T для системы (1)-(4) с краевыми условиями x(т) и x(T) = x(e) (T) e X⁽e)(T), т. е. нахождения следующего множества ⁷т, T

2.    Алгоритм формирования оптимального адаптивного терминального управления

оптимальных программных управлений путем реализации конечной последовательности алгебраических операций:

U ⁽ e) ( r^ T ,{ x ( т )}, X (1 ( T )) = { и ⁽ e ) ( • ) I и ⁽ e ) ( t ) e U ( t ), V t e^ - T - I,

' т , T

x ⁽ e ) ( t + 1) = A ( t ) x ⁽ e ) ( t ) + B ( t ) и ^{( e} ) ( t ) e G ( т , x ( т ); t + 1), x ⁽ e ) ( т ) e X 1 ( т )}.

Алгоритм оптимального адаптивного терминального управления расходом топлива жидкостной двигательной установки…

Пусть в дискретной динамической системе (1) – (4) сформирована τ-позиция

w ( e ) ( т ) = { т , x ⁽ e ) ( т )} e W ( т ) ( w (e) (0) = w ₀).

Тогда для те 0, T - 1 оптимальная адаптивная стратегия управления U ^e ) = U «e ) е U * формируется на основе применения метода прямых и обратных конструкций [3, 6] путем реализации следующей последовательности операций.

• 1.    Решения Задачи 1, т. е. вычисления множества

• 2.    На основании формул (13)–(15) первой части статьи вычисления множества управлений

• 3.    Выбора любого управления u⁽e) (т) е U«^e) (w⁽e) (т)).

• 4.    Вычисления по уравнениям нелинейного объекта (τ+1)-позиции:

• 5.    Если (т +1) < T -1, то осуществить переход на п. 1, иначе - на п. 6.

• 6.    Расчет числа с«^(0,T,w₀) = Уот(w₀,u^(e)(•)) — оптимального результата решения Задачи 2, соответствующего реализации управления u^(e)(•) = {u^(e)(t)}t_e0-T-1 e U(0,T), полученного посредством применения оптимальной адаптивной стратегии U^e) = U(e) е U« .

3.    Численный модельный пример решения задачи оптимального адаптивного терминального управления ДУ РН

U ( e ) ^ T , w ( т )) = U ⁽ e ) ^ T , { x ( т )}, X (1 (T )) e U^ T )

Y                                                                             'т, T и числа cYe)(т, T, w(т)) = Ф^ на отрезке времени т, T. Y                                       т, T

I « ) ( w ⁽ e ) ( т )) = U ⁽ e ) ( w ⁽ e ) ( т )) с U ₁( т ).

w ⁽ e ) ( т + 1) = { т + 1, x ⁽ e ) ( т + 1)}, x ⁽ e ) ( т + 1) = X ( т + 1; т , т + 1, x ⁽ e ) ( т ), u ⁽ e ) ( т )).

В работах [3, 6] доказано, что для линейных дискретных систем вида (1) – (3) предложенный алгоритм адаптивного управления, основанный на решении вспомогательных задач оптимального программного терминального управления методом прямых и обратных конструкций, является оптимальным алгоритмом адаптивного управления для терминального функционала вида (4).

Отметим, что предложенный алгоритм решения задачи оптимального адаптивного управления сводится к решению конечного числа задач линейного и выпуклого математического программирования, выполнения одношаговых операций над многогранниками и описания их с помощью вершин и конечных систем алгебраических равенств и неравенств, решения вспомогательных краевых задач.

Покажем эффективность предложенного подхода и соответствующих алгоритмов на численном примере, моделирующем решение задачи оптимального адаптивного терминального управления расходом топлива ДУ РН [8, 9]. Рассматривается нелинейная непрерывная управляемая система, описывающая динамику ДУ РН на промежутке времени [0, t ₁] уравнениями:

m ₍ t ) =   ( P + C 1 U ( t ) 2 + c 2 U ( t ))( K + U ( t ))

o     ( I + c 3 U ( t )² + c 4 U ( t ))(1 + K + U ( t )),

P + cU (t )2 + c2U (t) mf (t) =----------------------2--------------, f      (I + c3U (t )2 + c4 U (t ))(1 + K + U (t))

M o ( t ) = M 0 + A M o - f t ¹ m o ( t ) dt , t ₀

M f ( t ) = M f + AM_f - ^ t ¹ m_f ( t ) dt , с параметрами, заданными в табл. 1.

Таблица 1

Параметры исходной нелинейной системы

I , c	P , кг	K , б/р	Mo 0 , кг	M 0 f , кг	Δ M o , кг	Δ M f , кг
320	528 000	8/3	120 000	45 000	–500	300
Δ K , б/р	c 1 , б/р	c 2 , б/р	c 3 , б/р	c 4 , б/р	c 5 , б/р	t 1 , с
–1/25	8/75	–6700	9000	–15	–12	100

Исходной нелинейной непрерывной системе поставлена в соответствие аппроксимирующая линейная дискретная динамическая система, полученная посредством линеаризации вдоль опорной траектории вида траектории:

m^ (t) = mre (t) =

P · K

I + 1 • K ’

P

I + 1 • K ’

M Oe ( t ) = M 0

M fe ( t ) = M 0

P · K t ,

I + 1 • K

P t,

I + 1 • K

и дискретизации. Таким образом, аппроксимирующая рекуррентная векторно-матричная система, соответствующая (1), имеет вид

x(t +1) = A(t)x(t) + B(t)u (t), t e 0,15, где x(t) = {x1(t),x2(t),x3(t),x4(t)}eR4; x1(t) - расход окислителя ДУ РН; x2(t) - масса окислителя ДУ; xз(t) - расход горючего ДУ РН; x4(t) - масса горючего ДУ РН; u (t) e R1 - вектор управ ления; x(0) = xо = (1192.5,119 500,454,45 300)T - начальный фазовый вектор объекта управления; матрицы A(t) и B(t) стационарные и имеют следующие значения:

	' 1      0     0     0 '		Г 17 )
	- 6,25 1    0    0		0
A ( t ) =	,	, в ( t ) =		, V t e 0,15.
	0  0  10		- 12
	ч 0    0 - 6,25 1 у		. 0 ,

Фазовые ограничения ДУ РН для всех t e 0,16 имеют вид x1(t) e [1176; 1 224], |x2(t)| < 120 000, x3(t) e [432; 468], |x4(t)| < 46 000.

Качество процесса управления жидкостной ДУ РН оценивается значением выпуклого терминального функционала в момент времени T = 16, соответствующий моменту времени t 1 = 100 для начальной нелинейной непрерывной системы, значения которого вычисляются по формуле

Ф(x(T)) = ^(1200-x1(T))2 + x2(T)2 + K2(450-x3(T))2 + K2x4(T)2 , где первый и третий члены под квадратным корнем обозначают отклонение расходов компонентов топлива от требуемых значений, а второй и четвертый члены – количество топлива в баках жидкостной ДУ РН.

Решение задачи оптимального программного терминального управления для линейной дискретной системы реализовано с помощью алгоритма, приведенного в первой главе данной работы, и представляет собой формирование множества оптимальных управлений U ^(e) ( • ) = { u ^{( e} ’ ^j ) ( • )} j _ef^ , V j e 1, k : u ^{( e} ’ ^j ) ( • ) = = { u ^{( e} ’ ^j ) ( t )} t ₆ 0i5 , которое порождает соответствующие оптимальные траектории x ^{( e} ’ j ) ( • ) = x ( • ;0,16, x ₀, u ^{( e} ’ j ) ( • )), j e 1, k . Финальное состояние таких траекторий - x ( ^e ’ ^j ) (16) = x (16;0,16, x ₀, u ^{( e} ’ ^j ) ( • )), для всех j e 1, k есть вычисленный вектор x ^{( e} ’ ^j ) (16) = (1200.1, 38.97, 450.03, 10.5), который доставляет функционалу качества Ф минимальное значение Ф ^{( e} ) =Ф ( x ^{( e} ) (16)) = 47,988. Далее выбираются четыре программных управления

Шориков А.Ф., Калёв В.И.       Алгоритм оптимального адаптивного терминального управления расходом топлива жидкостной двигательной установки… u(e, j), j = 1,4 и подставляются в исходную систему (5), (6) для сравнения результатов реализации процедур программного и адаптивного управления.

Реше ни е з а да ч и о п ти мал ь но го адаптивного терминального управления нел и н е й но й сис т е м ой р еа л изо ва но с п о м о щь ю алгори тма, приведенного во второй главе данной раб о ты , и о п и сы в ае т с я множеством управлений U ⁽ e ) ( • ) = { U ae , j ) ( • ) } ._e 1d , V j e 1, d : U a^e , j ) ( • ) = {U a^e , j ) ( x ( t ))} t _G 0i5 . Для сравнен ия п олученн ы х р ез ул ьт а то в р е ализации программного и адаптивного управ л е ни я в р ас с м а тр ива е м о м пр и м е ре бы л и в ыбр а ны и подставлены пошагово в систему (5), (6 ) ч е т ы р е с тр а те г и и адаптивного управления u_a ^{( e , j )} ( x ( t )), j ∈ 1,4 . Проекции соответствующих траекторий представлены на рис. 1.

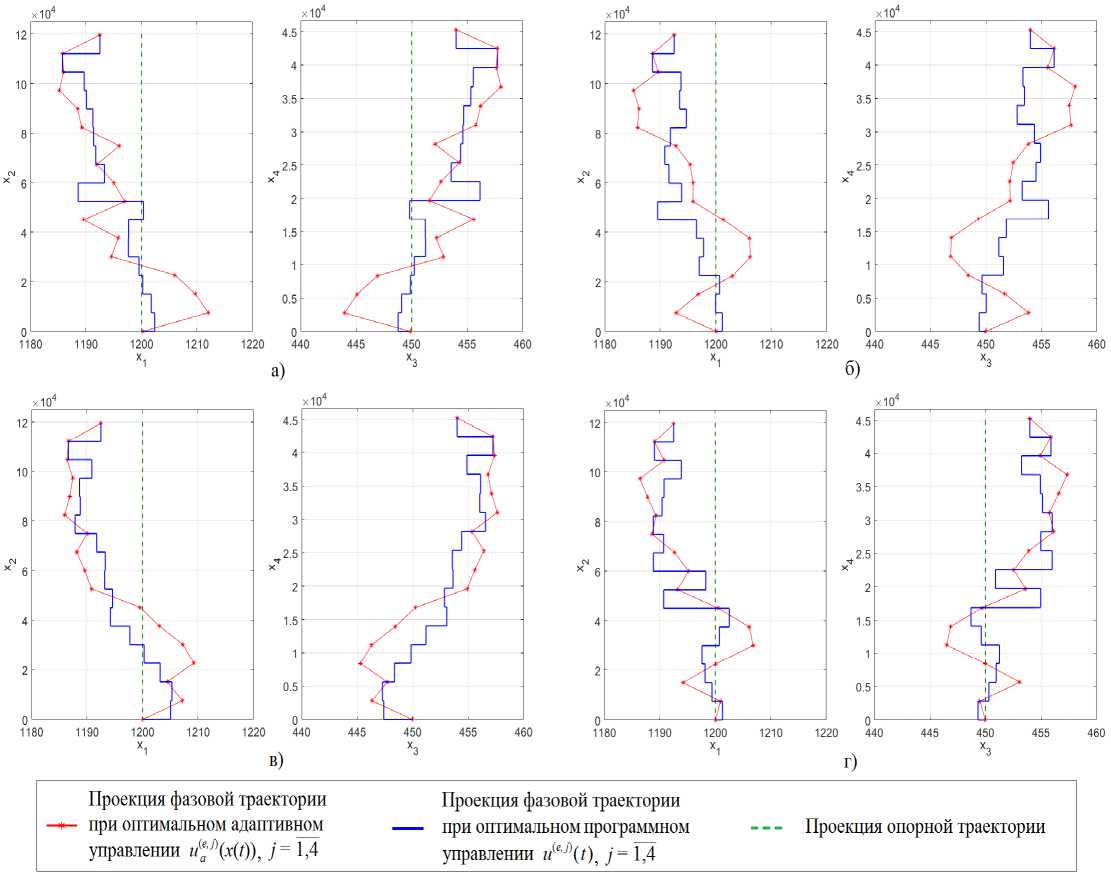
Рис. 1. Проекции фазовых траекторий при управлениях:

а) u ^{( e ,X)} и « ae ^,1) ; б) u ⁽ e ^,2) и « ae ^,2) ; в) u ⁽ e ^,3) и « ae ^,3) ; г) u ⁽ e ^,4) и « ae ^,4)

В табл . 2 пр и ве де н ы з н а ч е н и я функционала Ф для траекторий, соответст в ующ и х ре ал иза ция м о п тим а л ь ного п р огр ам м но го терминального управления линейной и нел ин е й но й с и с т е м а ми , а та к же ада п ти в н о г о т е р ми наль ного управления исходной нелинейной систем о й.

Пе р и о д вр е м ени м о делир о в ания для одного варианта решения задачи оп тим аль но го программного терм ин а л ь н о г о упр авления жидкостной ДУ РН составляет 0,4 с. Ве с ь пе р и о д вре м е н и м о д е л ир о ва н ия р еше н и я за да чи оптимального адаптивного терминального уп р а вл е ни я с о с тав ляе т 10 с. Из т а бл . 2 в и дн о , ч то дл я исходной нелинейной системы результат ре а л и з ации о п тим а л ьн о го ада п тивног о те рминал ьн о го управления лучше, чем результат реализ а ци и о п ти маль н ог о п р о гр а м м ного те р м и наль но го упра в л е н и я.

Таблица 2

Результаты решения модельного примера

	Управление	x 1 ( T )	x 2 ( T )	x 3 ( T )	x 4 ( T )	Ф( x ( T ))
Опорная траектория	u ( t ) ≡ 0	1200	0	450	0	0
Нелинейная система	u ( e ,1) ( t )	1200,1	39,1	450	10,6	48,261
	ua ( e ,1) ( x ( t ))	1200,2	32,7	449,9	8,5	39,837
	u ( e ,2) ( t )	1200,1	39,6	450	12,1	51,021
	u a ( e ,2) ( x ( t ))	1200,1	36,3	450	9,5	44,228
	u ( e ,3) ( t )	1200	38,7	450	9,6	46,339
	ua ( e ,3) ( x ( t ))	1200,1	31,1	450	8,2	37,935
	u ( e ,4) ( t )	1200,1	39,9	450	10,6	48,906
	u a ( e ,4)( x ( t ))	1200	36,6	450	10,1	45,372
Линейная система	u ( e , j ) ( t )	1200,1	39	450	10,5	47,988

Численное моделирование примера решения задач оптимального программного и адаптивного терминального управления жидкостной ДУ РН реализовано в среде MATLAB R2014a на ПК с Intel© Core™ i7-3770 CPU @ 3.4 GHz, 8 Gb RAM.

Заключение

В статье динамическая система управления расходом топлива жидкостной ДУ РН описана как нелинейная непрерывная дифференциальная система. Задача терминального управления расходом топлива жидкостной ДУ РН сформулирована как задача оптимального адаптивного терминального управления соответствующей аппроксимирующей линейной дискретной динамической системой. Для вычисления оптимального адаптивного терминального управления ДУ РН с нелинейной динамикой предложена процедура, основанная на реализации решения конечной рекуррентной последовательности вспомогательных задач оптимального программного терминального управления соответствующей аппроксимирующей линейной дискретной системой. Подробно описаны алгоритмы решения основной и вспомогательной задач оптимального управления. Показано, что задачу оптимального адаптивного терминального управления можно свести к решению конечного числа задач линейного и выпуклого математического программирования, выполнения одношаговых операций над компактными многогранниками и описания их с помощью вершин и конечных систем алгебраических равенств и неравенств, решения вспомогательных краевых задач. Результаты компьютерного моделирования показали применимость общего рекуррентного алгебраического метода построения областей достижимости и метода прямых и обратных конструкций [3] к решению задачи оптимального адаптивного терминального управления расходом топлива жидкостной ДУ РН.

Работа выполнена при финансовой поддержке РФФИ (проект № 18-01-00544).