Алгоритм оптимальной корректировки процесса развертывания сложных технических комплексов космической инфраструктуры

Рассмотрим процесс управления развертыванием сложных технических комплексов (СТК), функционирующих по жесткому временному регламенту. Оперативные характеристики развертывания СТК определяются требованиями вышестоящих уровней управления, а специфика задач, решаемых потребителями, может ограничить функционирование СТК пределами одного технологического цикла. На практике из-за влияния случайных или неучтенных факторов всегда существует риск не уложиться в заданный заказ-

чиком срок. Один из возможных подходов к расчету данных рисков заключается в последовательном уточнении значений вероятностей успешного выполнения задачи развертывания с учетом фактического времени, затраченного на предыдущие этапы.

Постановка задачи

Обозначим zпл плановое (нормативное) значение продолжительности всего цикла развертывания системы; ^ - продолжительность i-го этапа, i = (1, N), т. е. ^t™ = zпл- i=1

Будем полагать, что параметры распреде-

где

ления величин t_i

N

и

z = ^ t_f однозначно

связаны

с соответствующими директивными характери-

^Y z/T n ^{(v- 1 )}

- *

f ( v- l)^

1 ” ^{- ju} I t X t * I N -       (           \

= — J e ^ i = ² du * n j Ф / * ( x ; A(_K J dx •

^{2 n}-L                      i =v ^iV     '^i/7

стиками.

Пусть первый этап процесса развертывания * * пл был реализован за время ti , причем 11 > 11 , т. е. величина 11 > 1™ - это величина задержки (опоздания), и продолжительность выполнения задачи развертывания подлежит уточнению:

z _*

^z 1 = "Г = t 1 + t 2 + t 3 +- + t N [1]. t 1

Обозначим 1 — у t. = Rt. - риск невыполнения требований потребителя (заказчика) по сроку развертывания малогабаритной модульной квантово-оптической системы (ММКОС) «Сажень-ТА». Применив аппарат теории вероятностей, получим:

Задача оптимальной корректировки процесса развертывания формулируется следующим образом. Требуется определить такие значения Y _K вектора корректировок на каждом этапе, для которых минимизируются дополнительно привлекаемые ресурсы при ограничении на риск невыполнения задач развертывания в заданный срок [3].

^ s ( Y ( KЛ — YiKN} ) =

= ^^ s ^|V|( Y K ,) ) ^ mm i" ^s ( Y K ,y — Y KN-} ) (1) при ограничениях:

*    *

Y 1 ( t i , ^y ^0 ) = Y дир ;

z пл

Ф ^ = |ф z1 (t) dt, о где

1 ^ - ju ( ; - 1 * )

Y z 1 =     J e '   ddu * H e⁷ Ф z , ( x ; ^) dx .

^{2 П} -»                 i =2       '         '

*    * *

y 2 ( t i , t 2 , Y k^ ) = y дир ; ф 1 ₂ ( t ) = ф t ₂ ( t ,( A k ₂) ⁺ Y k_n^ ) ) ;

При невыполнении неравенства Y _t * ^ Y ди _P, где γ_дир – директивное значение, на оставшихся этапах необходимо проведение дополнительных оперативных мероприятий по обеспечению гарантированного выполнения задачи развертывания с требуемой вероятностью γ_дир в заданный срок z _пл. В результате этих мероприятий в конечном счете произойдет корректировка параметров A^K оставшихся этапов. В данной статье ограничимся рассмотрением корректировки только одного последующего этапа.

Обозначим Y^K дополнительно привлекаемые ресурсы, т. е. A^ _K ^ = A^ K ^ ⁺ ^ К^ ; f (^{2) -} функция зависимости стоимости A s ⁽²⁾ корректировки от значений дополнительных ресурсов, т. е. ДЛ = f ^{( 2}>( Yk. ) [2].

Тогда вектор корректировок должен обеспечивать выполнение равенства y _t = Y ди _р.

Пусть реализовано (ν – 1) этапов, т. е.

*        * *         -

• ^Y N - 1 ⁽ t i ’ ¹ 2,- • - , Y K N _1) ) = ^Y gup^;

• ^ф 1 N - 1 ^{( 1} ) = ^ф 1 n - 1 ( ¹ , ⁽ A K N - 1 ⁺ Y K N -2) ) ) •

Специфика данной задачи оптимизации (многоэтапность процесса, случайный характер исхода каждого этапа, зависимость исхода этапа от корректировки параметров распределения его продолжительности, аддитивность показателя (1) делают естественным обращение к алгоритмам стохастического динамического программирования для получения решения задачи. Для некоторых законов распределения величин t_t и небольшого числа этапов решение может быть получено аналитически. Покажем это на примере четырехэтапного процесса развертывания для варианта нормального закона распределения продолжительности величин t_i .

Параметр состояния

z

T*    - z ( v- ¹ )

( v- 1 )

(v-1) E *  ,      , ti + tv + —+ tN ’ i=1

тогда риск невыполнения задачи развертывания в заданный срок с учетом исхода (ν – 1)-го этапов определяется по формуле zпл

Ч. =¹ Ь' z/ Л) ⁽ t ) ^dt ’

Проведем следующие рассуждения. Пусть реализован первый этап, он продолжался t_Y единиц времени и вероятность Y 1 оказывается меньше заданной γ_дир.

Надо полагать, что стоимость дополнительных ресурсов, выделяемых и используемых на 2-м

этапе, пропорциональна величине «опоздания» ( t * - m 1 ) .

Пусть после корректировки параметров

M [ Y ”

, °[ ^ 2 ] реализован 2-й этап и Y 2 .

Том 2

Тогда стоимость дополнительно используемых на 3-м этапе ресурсов будет пропорциональна суммарной величине «опоздания»: ( t * - m 1 + t 2 - m 2 ) .

Аналогично, A s ( ^{4 )} ~ t * - m + t * - m ₂ + t * - m ₃.

Выберем в качестве параметра состояния x ˆ величину «опоздания». Это дискретная случайная

величина, принимающая значения:

x i = t * — m;

x₂ = t * - m 1 + 1 2 - m 2 ;           >.

x ₃ = t * - m 1 + 1 2 - m 2 + 1 ₃ * - m 3

Введем понятие «суммарного показателя за-

трат на корректировку», после реализации и корректировки третьего этапа он равен:

^12,3 (- ^ i , У 1 , y 1 , y 2 , y 2 ) =

^ (^ f l - y l . y ¹ ) *^ ⁴ ' ^Pl( ^X2 ■ y 2 ■ y² ) ■

где компоненты y ₂, y '₂ вектора корректировки на третьем этапе удовлетворяют равенству:

Алгоритм динамической корректировки

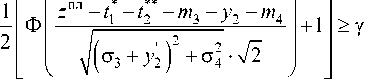
или

Вероятность своевременного информационного обеспечения с учетом исхода t_x первого этапа равна:

'                     * **

У 2 =V 2 ( У 2 , t 1 , t 2 ) • Аналогично рассуждая,

получим задачу

( 2 )      * пл *

A s^v ’ ~ t₁ - 1 1 = t 1 - m 1 ;

* 1

^Y i = 2

ф

le *

z 1 - 1 1 - m ₂ - m 3 - m 4 . 7°2+°fc4 • ² ,

+ 1

,

x

определения оптимальных (в смысле выбранного критерия) значений вектора корректировки. Заметим, что обратить в минимум величину ηˆ _2,3,4 нельзя, т.к. при любой нашей корректировке суммарные затраты П 2 з 4 (а также и затраты A ,S '^V' на каждом шаге) остаются случайной величиной. Однако мы можем выбрать такую корректировку, при которой среднее значение M ^1 1 234 ] стоимости дополнительно используемых ресурсов будет минимально [4, 5].

A/z,n о

При y₃< у :

'                                                                '                                                '

^m 2 = ^m 2 ⁺ У 1 , ° 2 =° 2 ⁺ У 1 ,

Функциядополнительных затрат

'T т.е. ^(K2) = »-•              <4>

Затраты на корректировку равны:

A s ⁽ ) = A s ⁽ Ч x_x,y_x,y_x ) , а компоненты вектора корректировки должны удовлетворять равенству

Пусть t_x = t_x . Чтобы «уложиться» в заданное время z ^пл, нужно каким-то образом распределить «опоздание» x 1 = t 1 — m 1 по оставшимся этапам. Если мы хотим компенсировать это «опоздание»

х j на втором этапе, то, очевидно, должны прово-

дить такую корректировку параметров распреде-

или

Ф

le *

^z 1 ^- t 1 ^{- m} 2 ^- У 1 ^{- m} 3 ^{- m} 4

'2  22

V(СТ2 + у1 ) +СТ3 +СТ4 • V22

+ 1

= Y

ления его продолжительност и , которая уменьшит

и математическое ожидание t 2 , и среднеквадрати-

ческое отклонение σ t ₂

т.е. должно быть:

-                       *

у =V | ⁽ У 1 - ' 1).■ ,      .

Пусть t 2 = t 2 = t 2⁽ y_x, y_x) . Вероятность

А t₂ = t ₂ - 1 ₂ <  0,

равна:

Ф

пл    ,*    ,**

z  — t i - 1 2 - m 3 - m 4

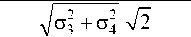
+ 1

**

= Y 2 .

При y *2* ^:

m 3 = m 3 ⁺ y 2 , ^ 3 =^ 3 + y 2 ;

T

Y k _3> = y 2 y 2 ;

A s ⁽³⁾=A s ⁽³⁾ ( X 2 , y 2 , y 2 ) .

**

Y 2

АО; = О; - О; <  0.

t ₂         t ₂        t ₂

При этом очевидно, что стоимость кор-

ректировки пропорциональна модулям величин

t ₂,σ _t ˆ ₂ ,

т. е. A s ⁽²⁾ ~ | r ₂|; A s ⁽²⁾

~

о, . t 2

Но A t 2 = У 1 , Ат t ₂ = y V

Можно доказать, что среднее значение суммарного показателя эффективности корректировки равно: х\_{2 34} ( x i ,^y 1 ,^y 1 ,^y ₂, ^y 2 , ^y 3 , ^y з ) =

= ]T c _v x x _v+ c _V ^A m y ² _v+ c ^ y V ,

V=1

где xi = t* -ml,y’l =V1 (y,ti*), x2 = xi + y, y 2 = ^2 ( У 2, 4, t 2** ) ,         (10)

'                  * ** ***

x 3 = x 2 + У 2 , У 3 =V 3 ( У 3 , t i , t 2 , t 3 ) •

Составление и решение рекуррентных функциональных уравнений

Сформулируем задачу оптимизации корректировки процесса развертывания для рассматриваемого примера. Требуется определить такие значения y 1 , y 1 , y ₂, y ₂, y ₃, y ₃ компоненты вектора корректировки на каждом шаге, которые дают минимум среднего суммарного показателя затрат на корректировку (10):

'            _'            _'

x i , У 1 , У 1 , У 2 ’ У 2 ’ У з , У з ) =

'__'__'

= min (xi’ У1, У1, У2, У2’ Уз, Уз ) = ц при ограничениях:

y’l =V 1 ( У 1 , t * ) ,

'                            **\

У 2 =V 2 ( У 2 , t l , t 2 ) ,

'                          ** ***\

У 3 =V 3 ( У 31 , t l , t 2 , t 3 ) •

Для отыскания решения задачи введем в рассмотрение функцию:

И N ( ^x ) = mn ^ 2,3, - , N ( x , У 1 , У 1 , - , y N - 1 , y N - 1 ) • (12)

Пусть μ₁( х ) – средние минимальные затраты на корректировку программы работ в одношаговой операции, начинающейся в состоянии х .

Для второго этапа (первого шага):

Ц 1 ( x ) = mill A s ⁽²⁾ ( x, У 1 y , y’l y )         (13)

У1 y. У1 y при У1 y =V1 (У1 y, tl).

Далее переходим к 2-шаговой операции:

ц2 (x ) =   min y 2 y (x). y 2 y (x)

A s ^{( 2 )} ( x , y 2 y , y 2 y ) + Ц 1 ( x 2 )

и к 3-шаговой операции, объединяя при этом 2-й и 3-й шаги в один шаг. Тогда в соответствии с принципом оптимальности

Ц 3 ( x ) = mini A s ⁽²⁾ ( x 2 , y 31 , y ₃₁ + Ц 2 ( x 2 ) ) (14) y 31 , y 3^' 1

при y 3 y =V 3 ( y 3 y , t l ) •

Величина μ2(х2) определяется так же, как μ2(х1), однако на вспомогательные переменные y21, y2′ 1 накладывается ограничение y2 1 = w 2 ( y21, t*, 12*), а на вспомогательные переменные y22, y22 ис- пользуемые для определения μ1(х3), – ограничение

* ** ***

y 22 = У з ( y 22 ’ t l ’ t 2 ’ t 3 ) •

P 2 ( x 2 ) = min Га S ^{( 3 )}( x 2 , y 21 , y 21 ) + Р 1 ( x 3 ) ! ;

y 21 , y 21 ^{L                                         J} I

* **

y 21 = ^ 2 ( y 21 , t l , t 2 ) , x 2 = ^x 1 + ^y 1 y .

Ц 1 ( x 3 ) = min A 5 ^{( 4 )}( x 3 , y 22 , y 22 ) ;

y ₂₂, y ₂₂

*  **  ***

^y 22 =^ 3 ( ^y 22 , t l , t 2 , t 3 ) , ^x 3 = ^x 2 + ^y22^.

Рекуррентные соотношения (14), (15), (16) соответствуют ретроспективной развертке (обратному ходу) алгоритма, а значения:

У з y ( x ) , У з y ( x ) , У 2 y = У 21 , У 2 y = = y 21, У 1 y ( x ) = y 22 , y ' 1 y ( x ) = y ' 22

являются условно-оптимальными значениями компонентов вектора корректировки [6].

Решив последовательно функциональные уравнения (14), (15), (16), при x = x 1 = t_x — m_x , определяем минимальные средние дополнительные затраты на развертывание:

μ= μ 3 ( х 1 ).                    (17)

Затем, построив прямую развертку (прямой ход алгоритма), определяем оптимальные значения компонент вектора корректировки [7].

Оптимальная корректировка на 2-м этапе:

^y i = ^y 3 ( x i ) , ^y ' 1 = ^y ' 3 ( x i ) .

Оптимальная корректировка на 3-м этапе:

y 2 = y 2 y ( » 1 ) , У З = УЗy ( * 1 ) .

Оптимальная корректировка на 4-м этапе:

^y 3 = y 1 y ( x l ) , y '3 = y '1 y ( X l ) .

Пример работы алгоритма

Рассмотрим пример работы алгоритма оптимальной корректировки процесса развертывания сложных технических комплексов космической

Том 2

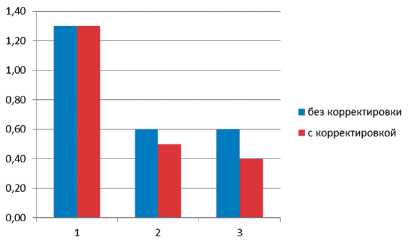
Рис. 1. Время этапов развертывания до и после корректировки

инфраструктуры. При помощи имитационного моделирования создадим две модели развертывания сложных технических комплексов космической инфраструктуры, таких как ММКОС «Сажень-ТА», при этом в одной из моделей будет применен алгоритм корректировки. Процесс развертывания данных комплексов согласно эксплуатационной документации производится в три этапа: 1) выбор места установки комплекса; 2) установка комплекса на выбранном месте; 3) настройка и начало работы комплекса. На каждом из этапов комплекс подвержен ряду случайных событий, замедляющих развертывание комплекса и приводящих к срыву плана по развертыванию. Согласно эксплуатационной документации время на развертывание составляет 2 часа: первый этап – 1 час, второй и третий этапы – по 30 минут, соответственно вероятность выполнения задачи за это время должна равняться 1. Средние вероятности событий, задерживающих развертывание, и время задержек были получены в ходе полевых испытаний и экс-

плуатационной практики. Проведем моделирование процессов развертывания по 200 раз, каждый без коррекции и с ней. Усреднённые результаты моделирования показаны на рис. 1.

Как видно из результатов, после корректировки плана развертывания время первого этапа развертывания превышает директивное на 30 %, как и без корректировки, а время второго и третьего этапов снизилось на 10 % и 20 % соответственно. Таким образом, время развертывания уменьшилось с 2,5 часа до 2,2 часа.

Заключение

Из вышеизложенного метода управления следует, что найденная оптимальная корректировка (18–20) является адаптивной и зависит от того, как будет развиваться случайный процесс развертывания.

Мы не определили жесткую «программу корректировки», но указали для каждой фазы процесса то «управление», которым следует отвечать на любой случайный исход предыдущей фазы.

Представленный алгоритм может быть переработан для других видов закона распределения продолжительности каждой из фаз, а также для вариантов с перестановкой этапов (например, вследствие изменения приоритетов или при целенаправленной рандомизации чередования фаз) [8, 9, 10]. Точность оценивания выигрыша от оптимизации в основном будет определяться степенью адекватности зависимостей, используемых при расчете затрат А s( v ) .