Алгоритм оптимизации расположения антенн базовых станций сотовой связи в сельской местности

В работе предлагается алгоритм оптимизации расположения антенн базовых станций (БС) сети сотовой связи на территории с низкой плотностью населения (сельская местность). За критерий оптимальности принимается максимальная площадь уверенного приема на местности при заданном числе(БС).

Постановка задачи

Определение оптимальной топологии сети сотовой связи в условиях сельской местности с низкой плотностью населения является актуальной задачей. В настоящий момент разработано достаточное количество методов и методик решения данной задачи [1]. Однако они носят статистический характер и позволяют разработать оптимальную топологию сети с некоторыми допущениями и погрешностями. Размещение БС сети сотовой связи будет оптимальным, если при определенном числе БС площадь уверенного приема будет максимальной. В статье приведены математические выражения и описан алгоритм, позволяющий оптимизировать расположение БС в условиях сельской местности.

Разработка математической модели алгоритма оптимизации

Для работы алгоритма в качестве входных данных необходимы следующие характеристики:

• -    трехмерная карта поверхности местности с учетом застройки;

• -    допустимые координаты и высоты антенн БС x,y,z (ограничения).

Перечисленные данные являются базой для оптимизации сети сотовой связи. В качестве целевой функции задачи оптимизации сети будем считать максимальную площадь уверенного приема на заданной местности с существующей застройкой при определенном числе БС.

Рассмотрим две поверхности [2], одной из которых является физическая поверхность местности со всеми элементами застройки, а вторая – поверхность, образованная пересечением фронта радиоволны БС с физической поверхностью. Если площади этих поверхностей равны между собой, то в этом случае на местности не существует зон затенения. При проектировании сети сотовой связи необходимо стремиться к этому варианту, который назовем идеальным.

Решение данной задачи можно произвести двумя методами. Первый метод – вычисление площадей поверхностей. Расчет реальной площади S0 местности с застройкой осуществляется численным методом по трехмерной карте местности в радиусе действия БС. Вторую поверхность – поверхность пересечения фронта радиоволны и физической поверхности SR рассчитаем геометрически, как это показано на рис. 1. Предположим, что имеем плоскую поверхность на некотором участке S0. На данном участке находится некоторая застройка, состоящая из зданий, среди которых имеется здание д1 и базовая станция БС, антенна которой излучает радиоволны. Лучи радиоволн пересекают здание д1 в точках a, b и с. Точка с принадлежит как зданию д1, так и поверхности S0.

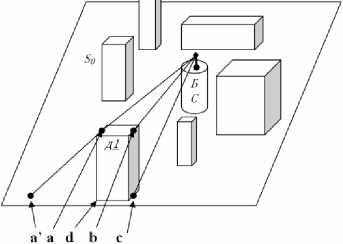
Рис. 1. К определению площади поверхности фронта радиоволны

Точка b принадлежит только зданию д1, точка a находится на краю крыши здания д1, и радиолуч, проходя точку a, пересекает поверхность S0 в точке a’. Из этого рисунка видно, что участок поверхности S0, ограниченный точками d и a’, не входит в площадь поверхности фронта радиоволны. Таким образом, суммируя площади по всем траекториям лучей радиоволн БС, можно определить общую площадь SR фронта радиоволны базовой станции и сравнить с площадью поверхности местности в радиусе действия БС. Недостатком этого метода являются значительные вычислительные затраты при реализации этого алгоритма на ЭВМ.

Второй метод основан на тензорном анализе, что позволяет снизить вычислительные затраты при вычислении площадей радиоволн SR. Для данной задачи можно считать, что имеем тензорное поле.

Вначале из четырехвалентного тензора кривизны получим двухвалентный тензор Риччи путем его свертки согласно [3]:

R^lLA- m где Rrj – тензор Риччи, Rry – тензор кривизны. Формулу (1) для тензора Риччи можно преобразовать к следующему виду:

trMAr <2)

Из тензора Риччи можно построить скаляр R по следующей формуле:

к^ХЛХ'^ m

Скаляр R(x\x") , определенный по (3), есть скалярная кривизна пространства поверхности в точке с координатами x',x². Скалярная кривизна – это полная свертка тензора кривизны R:

К = ^ХЛ^ <4>

Переход от компонент тензора Ry к скалярной кривизне R – это, на первый взгляд, потеря информации, так как девять величин (для трехмерного пространства) заменяются одной. Однако в двумерном случае никакой потери информации не происходит. Действительно, компоненты тензора кривизны R^kr кососимметричны как по верхней паре индексов, так и по нижней паре индексов. При совпадении k = r или i = j они становятся равными нулю. Единственные ненулевые n!2  n21 ol2 o21

компоненты – это Л^Л^Л^и K;_x, причем ^12 ⁼ ^21 ^{= —} ^12 ^{= —}^21’ Тогда в силу сказанного получаем:

R = Rl; + R;5 = 2R^_ .          (5)

Но согласно формуле Гаусса:

R = 2K,                        (6)

где K – гауссова кривизна. Рассмотрим рис. 2 [3]. Проведем касательную к поверхности плоскости P. Через точку M касания перпендикулярно этой плоскости рассечем поверхность двумя взаимно перпендикулярными плоскостями N₁ и N₂. На поверхности образуются две пересекающие в точке M кривые A₁MB₁ и A₂MB₂. Тогда средняя кривизна поверхности в точке М есть величина:

K = KA+K, = — + — ,

‘ rA r, где ^1 и A = - – радиус кривизны и кривизна '11

первой кривой в точке M; r2 И A = то же

„ J "'2

самое, но для второй кривой.

В случае сферической поверхности A = ' 2 = ^Г0

имеем К- . Подставим это в (6) и получим

Jo скалярную кривизну пространства в точке M как

го

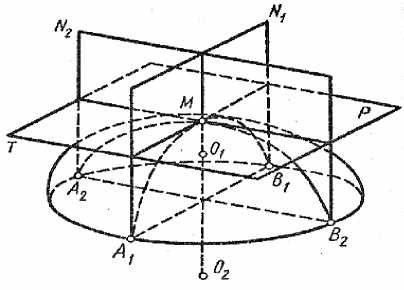
Рис. 2. Кривизна поверхности

Сравнивая скалярную кривизну, вычисленную для двух пространств по (9) в малой окрестности точки M (x1, x2, x3), определяем, совпадают ли поверхности в данной точке M. В случае несовпадения для лучей радиоволн БС происходит либо увеличение высоты антенны, либо перемещение БС по координатам x, y. Все расчеты проводятся с учетом зависимости распространения радиоволн от свойств земной поверхности.

Описание алгоритма

На основании вышеизложенного разработан алгоритм оптимизации расположения антенн БС, представленный на рис. 3. В начале программного модуля устанавливается число БС равное 1 (n = 1, блок 2). Далее (блок 3) из базы данных (база фактов) вводится рельеф и свойства местности.

Данные в этой базе представлены как координаты х, у, z. Координаты x, y отсчитываются от заданного начала координат. Значения высот z определяются как совокупные значения высоты рельефа и высоты зданий. Высоту определяем от минимальной высоты рельефа. Если использовать за нулевой уровень уровень моря, то могут иметь место отрицательные значения, что может привести к ошибке. В качестве исходных данных также вводится допустимое соотношение SR/S0 = D. Если D = 1, то имеется прием сигнала БС в любой точке заданной местности. Дополнительно для каждой БС задается допустимый диапазон изменения координат х, у, z.

В блоке 4 производится расчет площади местности с учетом застройки S0. В блоках 5 и 6

производится поиск координат x, y, принадлежащих точке, имеющей максимальную ординату z (максимальную высоту). Далее в блоке 7 уточняется, подходит ли выбранная точка для размещения БС с точки зрения возможности размещения в ней БС. Если ответ отрицательный, то ищется следующая точка с наибольшей высотой. В случае положительного ответа производится расчет площади описанной радиолучом (поверхность пересечения фронта радиоволны и физической поверхности) БС SR (блок 8).

В блоке 9 производится сравнение отношения SR/S0 с заданной допустимой величиной D. В случае если данное соотношение устраивает, то производится запись в выходную таблицу базы данных (блок 10). База данных включает: координаты базовой станции, площади S0 и SR и их соотношение, номер БС. На этом завершается оптимизация расположения БС (блок 11).

Если это соотношение S_R/S₀ не выполняется, то добавляется еще одна БС и n = 2 (блок 12). В блоке 13 производится выбор точки расположения второй БС. Выбор точки может происходить следующим образом: по следующему максимуму высоты z может задаваться вручную. В программе предусмотрено изменение координат (блок 17), если в выбранной точке нет возможности установить БС. Запрос о соответствии координат требованиям анализируется в блоке (14). В случае положительного решения производится расчет площади радиолуча от второй БС S_R(n) , которая складывается с площадью радиолуча от первой БС. Так как эта площадь будет увеличена за счет пересекаемых площадей от первой и второй БС, то в блоке (15) вычисляются и накапливаются две суммы: ^ΣSR(n) ^{и ΣS}пер(n) ^.

В блоке 16 происходит вычитание ΣSR(n) – ΣSпер(n) и вычисление отношения этой разности к площади местности с городской застройкой S0. Это отношение сравнивается с допустимым, и если оно меньше, то происходит изменение координат в блоке 17. Процесс повторяется в блоках 14-16. При этом для выбранного диапазона измеряется максимальное значение (ΣSR(n) – ΣSпер(n))/S0 (блок 16). Это и будут координаты очередной БС. Затем происходит запрос на установку следующей БС (блок 18). Если все БС установлены, то производится запись в таблицу выходных данных и программа заканчивает работу (блок 11). Если не все БС размещены, то значение n увеличивается на единицу (блок 19) и процесс повторяется с блока 13.

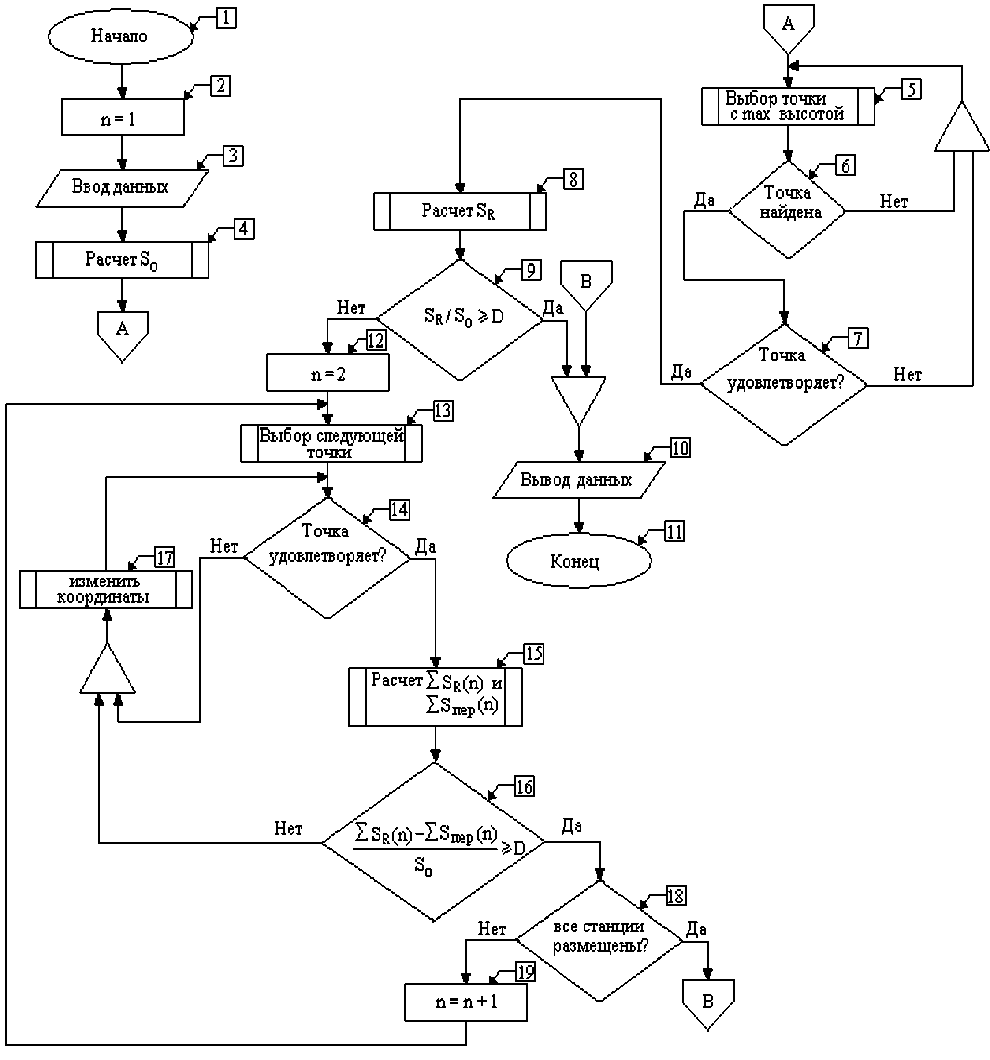
Рис. 3. Блок-схема алгоритма оптимизации

Выводы

На рис. 4 приведен фрагмент карты сельского района. На этой карте отмечено местоположение БС мобильной связи. С помощью вышеописанного алгоритма была произведена оптимизация изменения высоты антенн БС. Так, согласно полученным расчетным данным, увеличение высоты антенн БС на 10, 5, 12 м, а также их перемещение по местности позволило увеличить площадь уверенного приема на 15%. Достоверность решения поставленной задачи определяется точностью и качеством трехмерных электронных карт поверхности местности с ее застройкой.

Рис. 4. Фрагмент карты сельской местности

Литература 1.    Сорокин С.Н., Иванченко Е.В. Применение генетического поиска к решению задачи размещения базовых станций систем мобильной связи. http://library. mephi. ru /data /scientificsessions/2002/3/ 16.04.2010 2.    Логвинов А.В. Оптимизация числа базовых местности // ИКТ. Т.7, №2, 2009. – С.4145. 3.    Рашевский П.К. Риманова геометрия и тензорный анализ. М.: Наука, 1967. – 664 с. 4.    Чертов А.Г. Физические величины. Справочное издание. М.: «Высшая школа», 1990. – 336 с.