Алгоритм парирования сбоев в бортовых цифровых вычислительных комплексах со структурно-временной избыточностью

Бортовой цифровой вычислительный комплекс (БЦВК) современных космических аппаратов (КА) отвечает за реализацию логики работы КА, предназначен для управления вычислительными процессами между модулями, обработки телеметрической информации (информации о состоянии) аппарата, координации работы модулей КА, диагностики, устранения отказов и состоит из большого количества программно-аппаратных компонент. Элементная база БЦВК функционирует на предельных тактовых частотах. Это является причиной того, что интенсивность сбоев на порядок выше интенсивности отказов 10–9–10–10 1/с [1].

* © Викторов Д. С., Самоволина Е. В., 2018

Надежное функционирование БЦВК обеспечивается использованием разных видов избыточности: структурной, временной, функциональной, информационной, версионной [2, 3]. Наиболее распространена в БЦВК структурная избыточность, которая используется для парирования отказов. Комплексное использование структурной и временной избыточности позволяет распознавать и парировать не только отказы, но и сбои как программных, так и аппаратных компонент. Это особенно важно для БЦВК летательных аппаратов, к которым наряду с высокими требованиями к надёжности и достоверности контроля функционирования предьявляются довольно жёсткие ограничения на массогабаритные и энергетические характеристики.

Классические алгоритмы обеспечения надежного функционирования, которые базируются на структурной и временной избыточности, исследованы в работах [4-8] и др., однако их комплекс -ному использованию уделялось недостаточно внимания. Данное обстоятельство обусловливает необходимость разработки алгоритма обеспечения отказоустойчивости БЦВК на основе комплексного использования структурной и временной избыточности.

При разработке алгоритма парирования сбоев в БЦВК приняты следующие допущения: а) поток отказов всех элементов схемы простейший, последствия сбоев ликвидируются либо мажоритарными органами, либо повторным счётом участка программы обработки информации;

• б)    отказ любого элемента средств мажоритирова-ния, диагностирования и реконфигурации ведёт к отказу БЦВК;

• в)    интенсивности восстановления для отказов и сбоев являются неизменными;

• г)    восстановление сбившегося канала осуществляется путём повтора программы обработки информации с предыдущей точки восстановления (ТВ), при этом ТВ представляет собой периодически записываемое операционной системой в энергонезависимую память состояние всех полей основной памяти БЦВК.

Подобный подход применяется в большинстве известных работ по исследованию надёжности программно-аппаратных комплексов [1, 9, 10].

Предлагаемый алгоритм парирования сбоев представлен на рис. 1. Сущность алгоритма заключается в применении тестового контроля (ТК) и информации в ТВ (для защиты от сбоев) с различным доминированием в зависимости от количества исправных каналов.

Система начинает работу в трёхканальной конфигурации, при этом результатом вычислений является тот, который зафиксирован двумя каналами, при этом третий канал подвергается ТК. Если по результатам ТК канал признан исправным (сбой), то восстановление вычислительного процесса осуществляется по ТВ путём повтора последнего фрагмента программы обработки информации. При успешном восстановлении канала данные, характеризующие текущее состояние БЦВК из любого исправного канала, записываются в ТВ восстановленного канала.

В случае идентификации ТК отказа канала БЦВК реконфигурируется в двухканальную архитектуру.

В двухканальной конфигурации осуществляется периодическое сравнение результатов обработки данных в каналах. При несовпадении результатов вычислений оба канала прекращают обработку информации и предпринимается по- пытка восстановления обоих каналов по ТВ путём n-кратного повторения вычислений с предыдущей ТВ. Если в результате этой операции удаётся получить одинаковые результаты вычислений в двух каналах, то БЦВК продолжает функционировать в двухканальной конфигурации (сбой в канале). В противном случае (отказ канала) оба канала подвергаются ТК с целью выявления отказавшего, который исключается из конфигурации, и БЦВК переходит на функционирование в одноканальной конфигурации.

Функционирование в одноканальной архитектуре предполагает наличие средств встроенного контроля для выявления неисправности канала. При получении сигнала от средств встроенного контроля о неисправности канала (сбой) осуществляется попытка его восстановления по ТВ путём с- кратного повторения фрагмента программы обработки информации. Если средства встроенного контроля обнаружат, что неисправность ликвидирована, то БЦВК продолжит обработку информации. При исчерпании лимита повторов фрагмента программы БЦВК признаётся отказавшей.

Таким образом, комплексное применение ТК и восстановления по ТВ с различным преобладанием в зависимости от количества исправных каналов позволяет классифицировать неисправности как сбой и отказ, что позволяет избежать неоправданного расхода резервных ресурсов и, следовательно, повысить надёжность БЦВК.

Проведём количественную оценку прироста надёжности от применения предложенного выше алгоритма, для чего разработаем модели надёжности БВС. При разработке модели примем дополнительное допущение об экспоненциальном законе распределения времени до отказа.

Принимая во внимание принятые допущения, математическая модель, описывающая поведение БЦВК для предложенного алгоритма, может быть описана марковской цепью с непрерывным временем и следующими дискретными состояниями:

• S 0    - БЦВК исправно функционирует в 3-канальной конфигурации;

• S 1    - БЦВК копирует данные, характеризующие текущее состояние трёх исправных каналов в ТВ;

• S ₂    - БЦВК восстанавливает неисправный канал по ТВ;

• S ₃    – отказ одного канала;

• S ₄    - БЦВК исправно функционирует в 2-канальной конфигурации;

• S ₅    - БЦВК копирует данные, характеризующие текущее состояние двух исправных каналов в ТВ;

• S ₆    - БЦВК восстанавливает вычислительный процесс двух каналов по ТВ;

  
  

Том 2

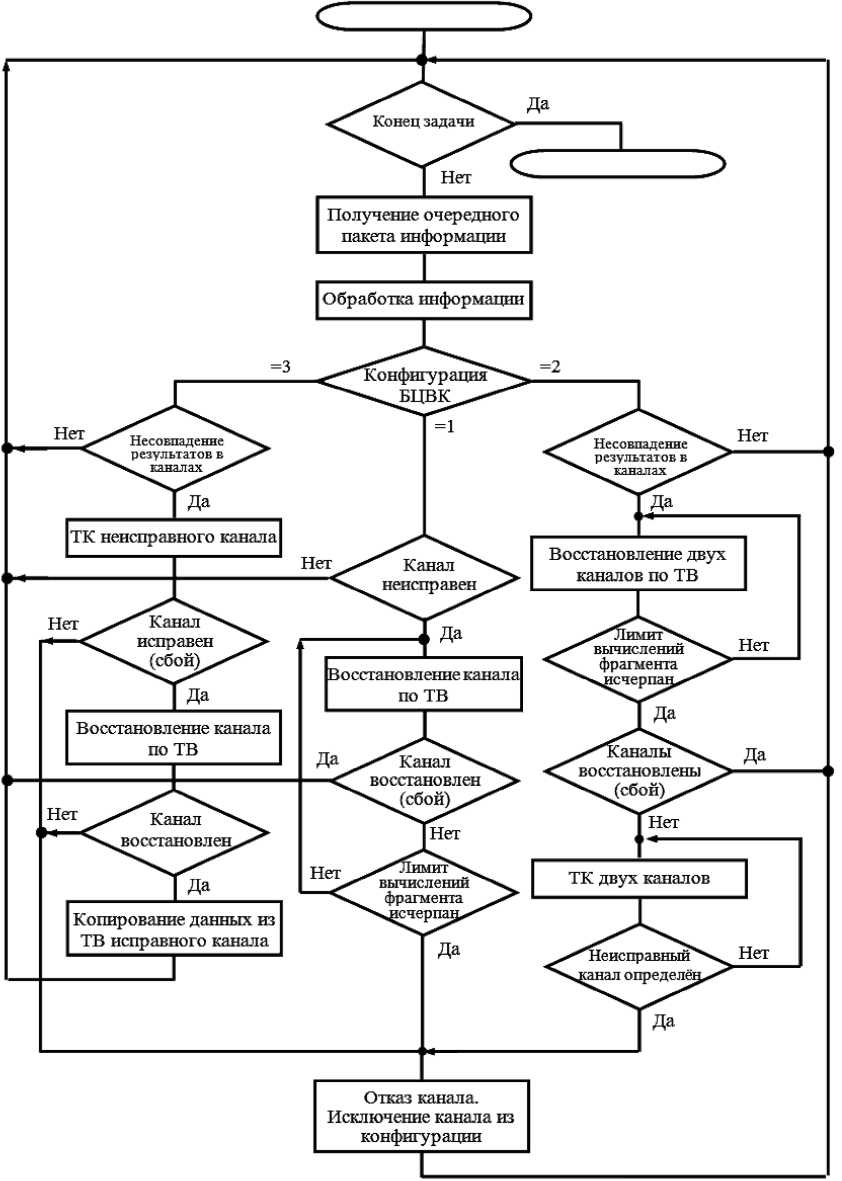
Рис. 1. Алгоритм парирования сбоев в БВС

• S ₇    – отказ второго канала;

• S ₈    – БЦВК исправно функционирует в 1-канальной конфигурации;

• S ₉    – БЦВК копирует данные, характеризующие текущее состояние исправного канала в ТВ;

• S ₁₀    – по сигналу от встроенных средств контроля БЦВК восстанавливает вычислительный процесс в канале по ТВ;

• S ₁₁    – встроенные средства контроля БЦВК выявили неисправность канала, и осуществляется попытка его восстановления функционирования путём с -кратного повторения вычислений с последней ТВ;

• S 12    – отказ БЦВК.

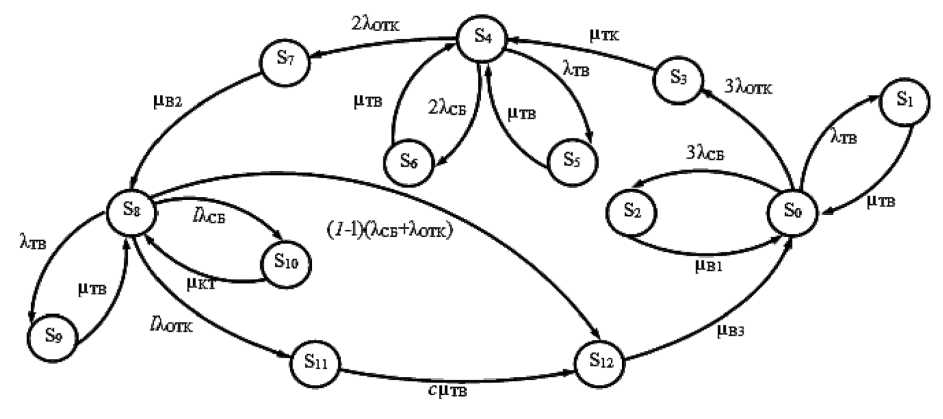
Граф переходов БЦВК, учитывающий интенсивности переходов, приведен на рис. 2.

В соответствии с методикой расчёта марковских процессов имеем следующую систему уравнений:

Ро ( t ) (И = - Р 0 ( t )З Х сб - Р о ( t )З Х отк - P ,( t ) Х тв +

⁺ Р ⁽ t ) Р т_В + Р 12 ⁽ t ) Р вз ⁺ P 2 ⁽ t ) Р в1 ^;

P 1 ( l )/ dl = - Р 1 ( t ) ц тв + Р о ( t ) Х тв ;

P 2 ( l )/ dl = - Р ₂( t ) Р в1 + Р о ( t )З Х сб ;

Р з ( l )/ dl = - Р з ( l ) Р т_К + P o ( l )3 X ОТ _К;

P ₄ ( l )/ dl = - Р ₄ ( t )2 X отк - Р 4 ( t )2 Х сб - Р 4 ( t ) Х тв +

^{+ Р} 3 ⁽ t ^TK ^{+ Р} 5 ⁽ t ) Н тв ^{+ Р} 6 ⁽ t ^тв ^;

^p( l )/ dl = - Р 5 ( t ) Р тв + Р 4 ( t ) X тв ;

Р б ( l )/ dl = - Р ₆( t )^ + Р 4 ( t )2 Х сб ;

P ₇ ( l )/ dl = - Р ₇ ( t ) P B2 + Р 4 ( t )2 X отк ;

P 8^{( l} V ^dl = ^{- Р} 8⁽ t X^X СБ ^{- Р} 8 ⁽ t ^{) X} TB ^{- Р} 8 ⁽ t ) ^ ^X OTK ^-

• -    Р 8 ( t )(1 - ^ )( Х сб +X отк ) + Р 9 ( t ) Р тв +

⁺ Р ^{1о (} t ^{) ц тВ + Р 7 (} t ^{) ц В2 ;}

P 9 ^{( l} )/ ^dl = ^{- Р} 9 ⁽ t ) ^ TB ^{+ Р} 8 ⁽ t ^{) X} TB ^;

P 10 ( l )/ dl = - Р 1о ( t ) Р тв + Р 8 ( t XX СБ ;

P 1^{( l} )/ ^dl = ^{- Р} 11⁽ t ) c Ц тв ^{+ Р} 8 ⁽ t ) ^ ^X отк ^;

P 2 ^{( l} )/ ^dl = ^{- Р} 12 ⁽ t ) ^ B3 ^{+ Р} 8 ⁽ t ^{)(1 -} ^ ^{)( Х} СБ ^{+ X} ОТК ) ⁺

+ Р11( t) c pTB, где Цв1 =            т ; Цв2 -          ; Цв3 =

Т ТВ-ТВ        Т ТВ + Т ТК тв + тк + рВ1 характеризует интенсивность восстановления трёхканальной БЦВК и предполагает проведение ТК неисправного канала с целью определения вида неисправности, повтор фрагмента программы обработки информации с последней ТВ и копирование данных, характеризующих состояние системы из исправного канала в восстановленный.

рВ2 описывает интенсивность восстановления двухканальной БЦВК и включает повтор фрагмента программы обработки информации с последней ТВ и проведение ТК обоих каналов для выявления отказавшего.

рВ3 характеризует интенсивность восстановления БЦВК после отказа последнего канала и предполагает рестарт системы.

В системе уравнений приняты следующие обозначения:

Р ₀ – вероятность безотказной работы БЦВК в трёхканальной конфигурации;

Р 1 - вероятность нахождения БЦВК в состоянии формирования ТВ;

Р ₂ - вероятность возникновения сбоя в одном канале;

Р ₃ – вероятность отказа одного канала;

Р ₄ – вероятность безотказной работы БЦВК в двухканальной конфигурации;

Р ₅ - вероятность нахождения БЦВК в состоянии копирования ТВ;

Р 6 - вероятность возникновения сбоя в канале при функционировании БЦВК в двухканальной конфигурации;

Р ₇ - вероятность отказа канала при функционировании БЦВК в двухканальной конфигурации;

Р ₈ - вероятность безотказной работы БЦВК в одноканальной конфигурации;

Р 9 - вероятность нахождения БЦВК в состоянии копирования ТВ;

Р ₁₀ - вероятность возникновения сбоя в канале;

Р 11 - вероятность восстановления функционирования канала путём с -кратного повторения вычислений с ТВ;

Р ₁₂ - вероятность отказа БЦВК;

T _TВ – временной интервал, необходимый для формирования ТВ;

T _TК – время, затраченное на тестирование канала;

T _TВ–TВ – временной интервал между двумя соседними ТВ;

T _Ц – время цикла обработки информации.

Решая систему уравнений, следует учитывать, что модель описывает все возможные состо-n яния БЦВК, а следовательно, ^ Pi = 1. Из систе-i=1

мы уравнений можно вычислить вероятности нахождения БЦВК в любом возможном состоянии P_i ( t ). Для БЦВК КА представляет интерес оценка вероятности безотказной работы за время t , которая вычисляется по формуле

P (t)=2 P (t), i е E где E – множество работоспособных состояний БЦВК, в которых система осуществляет обработку информации.

Предложенная модель предполагает применение идеальных по достоверности и безотказности средств встроенного контроля, что даёт весьма приблизительные результаты при оценке безотказности.

Значительный рост тактовых частот привёл к тому, что в ходе тестирования каналов может быть ошибочно классифицирован вид неисправности, т. е. сбой воспринят как отказ и наоборот. Для учёта ошибочной классификации вида неисправности в граф (рис. 2) добавлены следующие переходы:

S 3 ^ S 0 и S ₇ ^ S 4 , интенсивность которых D 2 Ц Тк (характеризуют такое состояние БЦВК, при котором ТК классифицировал отказ канала как сбой);

S ₂ ^ S 4 и S ₆ ^ S ₈, интенсивность которых D з Мг К (означает, что ТК классифицировал сбой канала как отказ).

Том 2

При этом граф переходов БЦВК с учётом ошибочной классификации вида неисправности примет вид, представленный на рис. 3. Дискретные состояния в данном графе аналогичны графу на рис. 2.

Принимая во внимание методику расчёта марковских процессов, получим следующую систему дифференциальных уравнений:

Р о ( t )/ dt = - Р о ( t )3 X СБ - Р о ( t )3 X отк - P o (t ) X ТВ +

⁺ Р ⁽ t ) Ц тв ⁺ P ⁽ t ) D 2 ^ ТК ^{+ Р} 12 ⁽ t ) Ц В3 ⁺

⁺ P ⁽ t ) Ц в1 ;

Р 1 ( t )/ dt = - Р , ( t ) Ц тв + Р о ( t Атв ;

P 2 ( t )/ dt = - Р 2 ( t ) D ^i - P 2 ( t ) D 3 ^ TK + Р о ( t )3 X СБ ;

Р з ( t )/ dt = - Р з ( t ) Р тк + P o ( t )3 X отк ;

P ₄ ( t )/ dt = - Р ₄ ( t Жотк - Р 4 ( t )2 Х сб - Р 4 ( t ) X ТВ +

^{+ Р} 3 ⁽ t ) ^D 1 ^ TK ^{+ P}2 ⁽ t ) ^D 3 ^ TK ^{+ Р} 5 ⁽ t ) Н тВ ⁺

^{+ Р} 6 ⁽ t ) Р ТВ ^{+ P} 7 ⁽ t ) D 2 ^ TK^;

P 5 ( t >/ dt =- Р 5 ( t ) Р тв + Р 4 ( t ) X ТВ ;

Р б ( t )/ dt = - Р б ( t ) Р тв - Р б ( t ) D 3 P TK + Р 4 ( t )2 X сб ;

P ₇ ( t )/ dt = - Р 7 ( t ) D i P b2 - P 7 ( t ) D 2 Р тк + Р 4 ( t )2 Х отк ;

P ₈( t )/ dt = - Р ₈( t Жсб - Р 8 ( t ) Х тв - Р 8 ( t) I X отк -

• -    Р 8 ( t )(1 - ^ )( Х сб +Х отк ) + P 7 ( t ) D 1 P В2 +

⁺ P 6 ⁽ t ) ^D 3 ^ TK ^{+ Р} 9 ⁽ t ^ТВ ⁺ Р 10 ⁽ t ) Р ТВ ^;

P ₉ ( t )/ dt = - Р 9 ( t ) Р тв + Р 8 ( t ) X ТВ ;

P 1o ( t )/ dt =- Р 1 ₀( t ) Ц тв + Р 8 ( t Жсб ;

P 1 ⁽ t )/ ^dt = ^{- Р} 11⁽ t ) c Ц тв ^{+ Р} 8 ⁽ t ) ^ ^X OTK^;

P12 (t)/dt = - Р12 (t )Рвз + Р8 (t )(1 - £)(Хсб +Хотк ) + где D! - вероятность правильной классификации неисправности ТК; D2 - вероятность того, что ТК классифицировал отказ как сбой; D3 – вероятность того, что ТК классифицировал сбой как отказ.

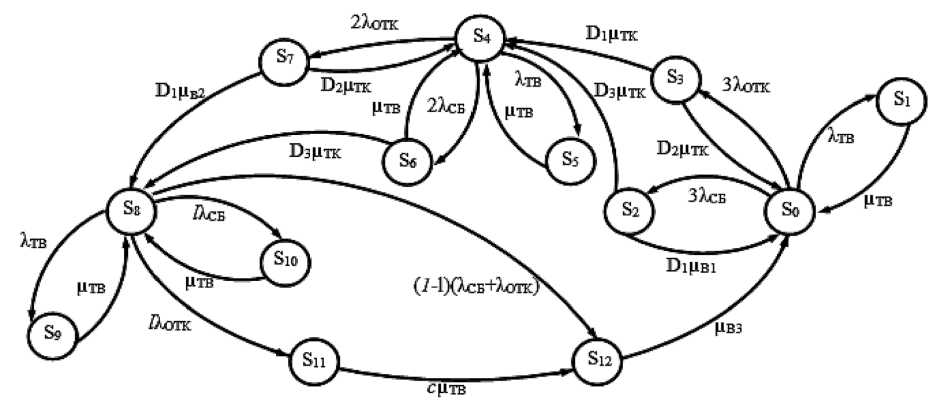
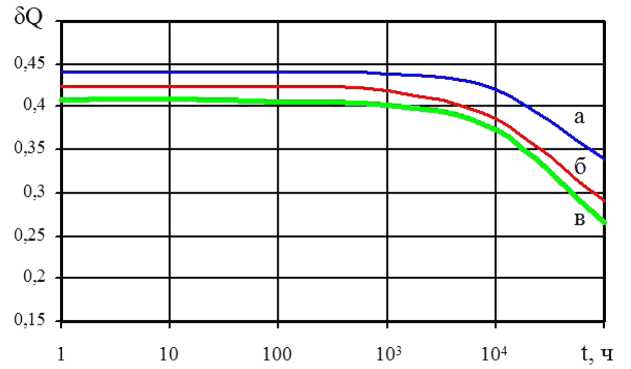
Рис. 4. Зависимость относительного выигрыша в снижении вероятности отказа при: а) D1 = 1, D2 = 0, D3 = 0; б) D1 = 0, D2 = 1, D3 = 0; в) D1 = 0, D2 = 0, D3 = 1

При моделировании значения переменных означают достоверность тестового контроля - D 1, D ₂, D 3 могут принимать значения 0 или 1.

В системе уравнений вероятности P ₀, P 4 , P ₈ характеризуют безотказную работу БЦВК в трёхканальной, двухканальной и одноканальной конфигурации соответственно.

Анализ системы уравнений позволяет предположить, что при увеличении λ_ТВ увеличиваются значения вероятностей P ₀, P 4 , P ₈ и БЦВК сохраняет работоспособность при любом количестве сбоев.

Учитывая, что в работе рассматриваются БЦВК КА, безотказность которых лежит в диапазоне 0,9…0,999, в качестве показателя для оценки эффективности разработанного алгоритма целесообразно применять показатель – относительный выигрыш δ Q в снижении вероятности отказа.

8 Q = Q^Q, Qo где Q - вероятность отказа БЦВК, реализующего предложенный метод структурно-временного резервирования;

Q ₀ - вероятность отказа БЦВК, относительно которой определяется относительный выигрыш δ Q в снижении вероятности отказа.

Следует учитывать, что БЦВК КА рассматриваются как невосстанавливаемые системы, поэтому согласно [2, 3] относительный выигрыш в снижении вероятности отказа целесообразно рассчитывать так:

„„ Q o - ( 1 - [ Po + P 4 + P ] )

Q Q o .

В свою очередь, за Q ₀ примем вероятность отказа трёхканальной БЦВК без ТК и восстановления по ТВ, численные значения которых получены в [5].

На основании анализа данных об отказах и сбоях в БЦВК [1, 3] для моделирования были выбраны следующие базовые значения: Х_ОТК = = 10^–8 1/ч; λ_СБ = 10^–9 1/ч; λ_ТВ = 10³ 1/ч; μ_ТК = 10⁴ 1/ч; μ ТВ = 5·10 –5 1/ч, T ТВ = 10 –4 ч, T ТВ–ТВ = 10 –3 ч, T _ТК = 10^-4 ч, T ц = 5^10 ³ ч. Результаты моделирования зависимости относительного выигрыша в снижении вероятности отказа от времени эксплуатации при различной достоверности контроля представлены на рис. 4.

Результаты моделирования показали, что применение предложенного алгоритма позволяет повысить (до 45 % по показателю 5 Q - относительный выигрыш в снижении вероятности отказа) надежность трёхканальных БЦВК со структурно-временной избыточностью.

Предлагаемый алгоритм ориентирован на идентификацию и парирование сбоев и отказов. Алгоритм может применяться в любых БЦВК с межканальными связями. Для его реализации необходимо обеспечить синхронную работу каналов БЦВК. Всё вышеперечисленное позволяет осуществить эффективную практическую реализацию предложенного алгоритма при жёстких ограничениях на массогабаритные и энергетические характеристики.