Алгоритм подбора коэффициентов для метода поиска устойчивых закономерностей на интервалах временного ряда

Практически каждый процесс, происходящий в мире, может характеризоваться как минимум двумя параметрами: моментом времени, в который он произошел, и численным значением события, которое произошло в этот момент времени. Особенностью данных процессов является то, что полученные в результате наблюдения данные можно представить в виде специальной математической структуры – временного ряда.

Под временным рядом понимают набор из последовательно измеренных через некоторые (чаще равные) промежутки времени данных. Временной ряд имеет два обязательных атрибута: временное значение – значение времени в момент, когда происходило измерение данных, и непосредственное значение данных в момент времени.

В настоящее время существует большое число методов для исследования временных рядов. У каждого из методов есть свои достоинства и недостатки, поэтому для решения конкретной задачи исследователем должен подбираться метод, наиболее точно учитывающий ее специфику. Так как формальный алгоритм отыскания метода исследования временного ряда отсутствует, этот процесс происходит эмпирическим путем, основываясь на опыте исследователя или общих рекомендациях.

Автор работы [1] В.В.Бурмистров рассмотрел различные интервалы многих биржевых процессов и выдвинул гипотезу о том, что зависимости, составленные из переменных на отдельном интервале временного ряда, равны среднему значению этого интервала. В работе экспериментально доказано, что данные зависимости фрактальны на всех исследуемых интервалах в пределах статистический погрешности(отклонения близки к белому шуму).

Основываясь на работе [1], был разработан метод поиска устойчивых закономерностей на интервалах временного ряда. На основе полученных зависимостей можно сделать вывод о дальнейшем их существовании в рассматриваемом процессе, что позволяет предсказать значения временного ряда на заданный интервал времени.

Одной из важных частей разработанного метода является подбор таких коэффициентов к 1 и к₂ , благодаря которым становится возможно равенство зависимостей F 1 , F 2 , F_cp .

Алгоритм подбора коэффициентов k1 и k2 для зависимостей F1, F2

Метод поиска устойчивых закономерностей на интервалах временного ряда базируется на формировании зависимостей F 1 , F 2 , F_cp :

р _ С^)

^F ,

^ 2

J^yto

^Lmm к г     ^,

F = ср

5!^ t m -t n

где tm - точка начала интервала, tn - точка конца интервала, tmax - точка, в которой функция принимает максимальное значение на интервале, tm^n -точка, в которой функция принимает минимальное значение на интервале, к1 и к2 - вспомогательные коэффициенты, благодаря которым существует равенство F1 = F2 = Fcp.

Разработанный алгоритм позволяет привести зависимости, сформированные по формулам (1-3) для каждой длины интервала ki к виду к1    кг    ^ср •

В работе участвуют два массива - ArrXY, эталонный массив, и массив ArrXY_2, значения которого при умножении на коэффициент k будут стремится к значениям массива ArrXY. Выполняется функцию Delta, на вход которой подается длина массивов N и массивы ArrXY и ArrXY_2. Выполняется цикл, пока не будут пройдены все значения диапазона [resultDelta; resultDelta] с заданным шагом. В цикле выполняется функцию Koeff. В результате получаем количество точек, которые совпадают у эталонного массива со вторым массивом, умноженным на переменную цикла с заданной погрешностью. Если количество точек, больше чем в предыдущей итерации цикла, то переменная перезаписывается. Конечный результат работы - коэффициент k, при котором умноженные на k элементы второго массива максимально совпадают с элементами эталонного массива.

Общая блок-схема разработанного алгоритма представлена на рисунке

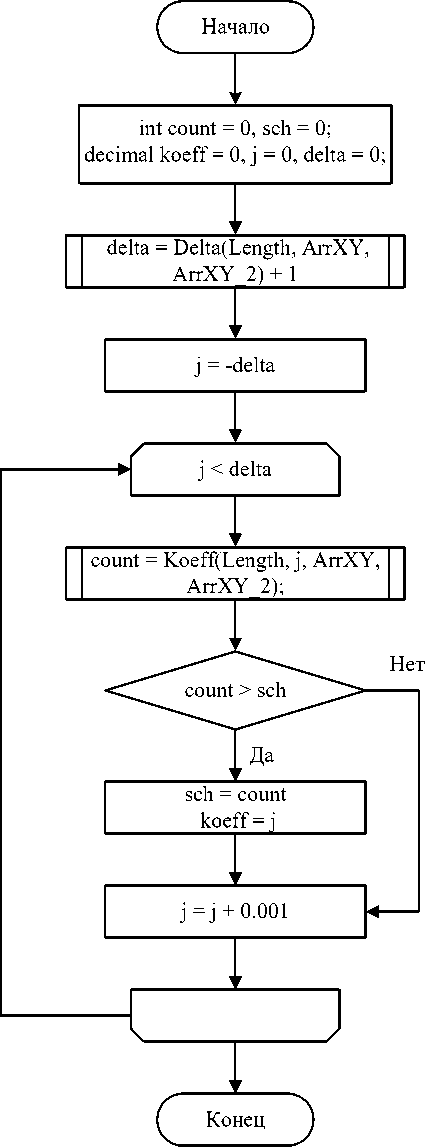
Рисунок 1 - Блок-схема расчета коэффициентов к 1 и к₂ .

Блок-схемы функций Delta и Koeff приведены на рисунках 2- 3.

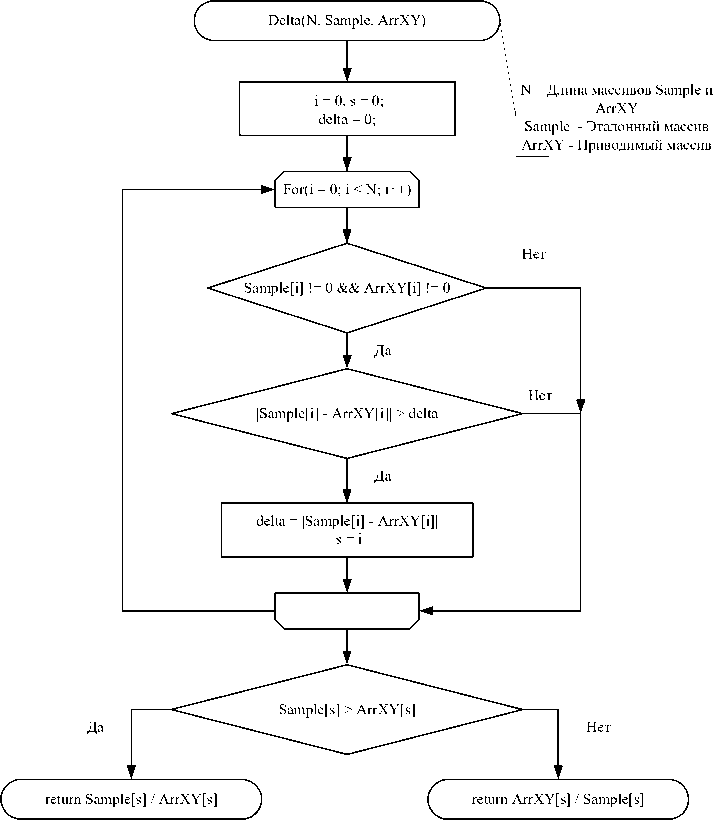
Рисунок 2 - Блок-схема алгоритма функции Delta.

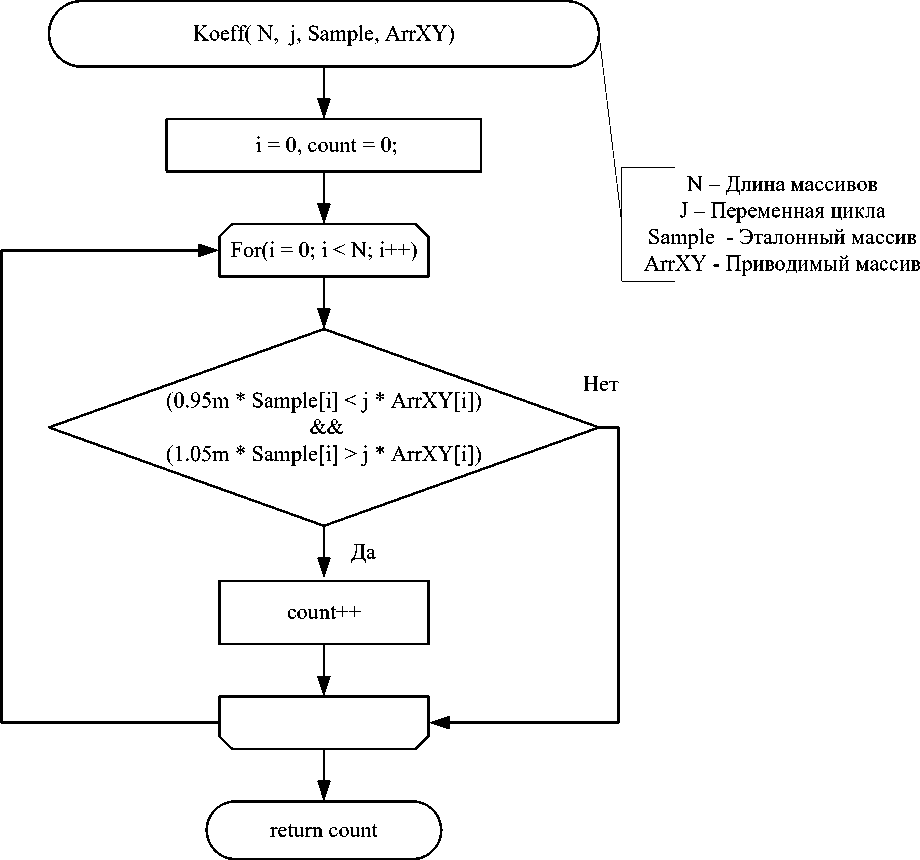
Рисунок 3 - Блок-схема алгоритма функции Koeff

Результаты работы разработанного алгоритма

На рисунке 4 приведен исследуемый временной ряд.

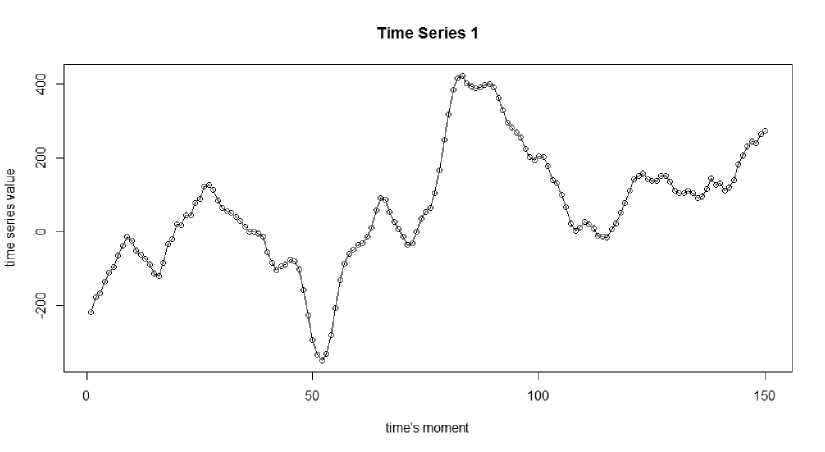
Рисунок 4 - Исследуемый временной ряд

Проведем формирование зависимостей F 1 , F 2 , F ср по формулам (1-3) при длине интервала k = 4, рассчитаем корреляцию между ними и построим график этих зависимостей. Соответствующие графики представлены на рисунках 5 - 6.

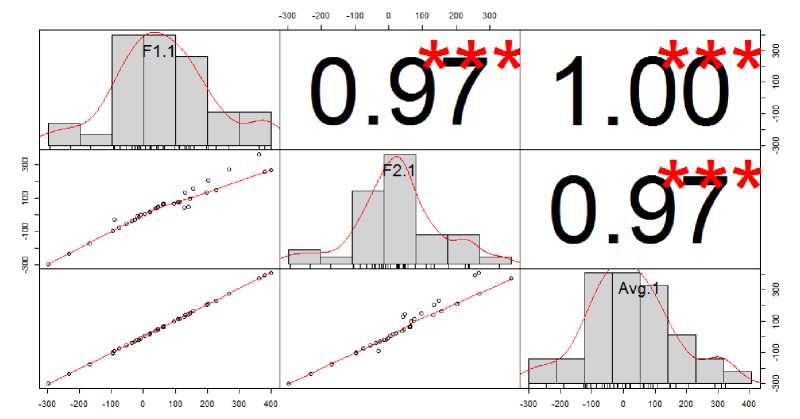
Рисунок 5 - График корреляции между зависимостями F 1 , F 2 , F ср

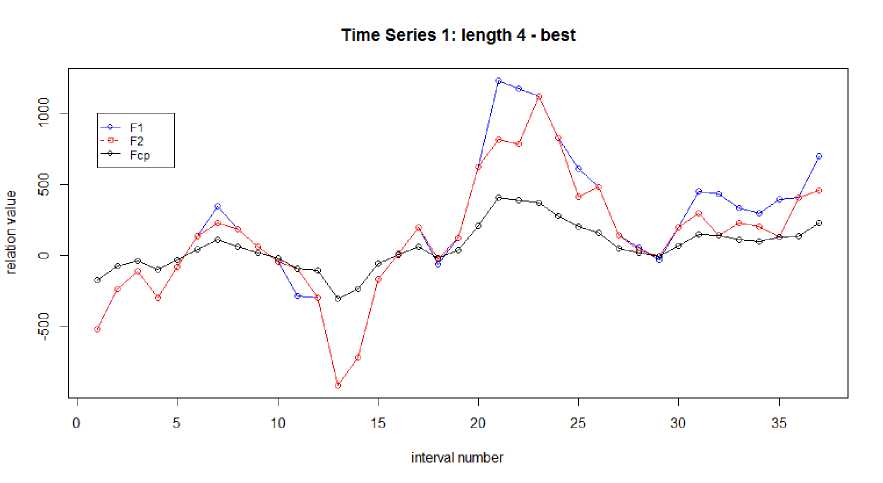
Рисунок 6 - График зависимостей F 1 , F 2 , F ср для рассматриваемого временного ряда при k = 4 без подбора коэффициентов.

Программно рассчитаем коэффициенты k₁ и k_2, основываясь на предложенном алгоритме. Полученные значения составят 0,325 и 0,325 для k 1 и k 2 соответственно. Построим график зависимостей F 1 , F 2 , F ср с учетом коэффициентов. Соответствующий график представлен на рисунке 7.

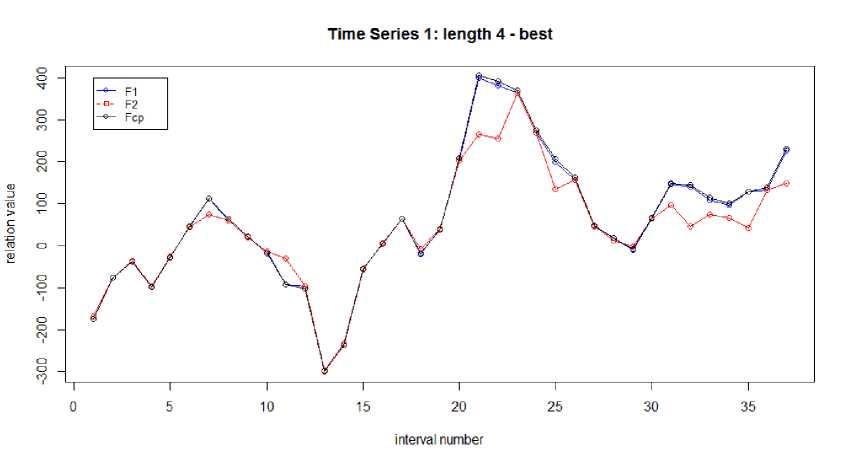
Рисунок 7 - График зависимостей F₁, F₂, F_ср для рассматриваемого временного ряда при k = 4 при подборе коэффициентов.

Выводы

На основании полученных графиков можно сделать вывод, что с помощью предложенного алгоритма возможен корректный подбор значений коэффициентов k 1 и k 2.