Алгоритм поиска оптимального плана решения транспортной задачи в сетевой форме

Рассмотрим классическую транспортную задачу с поиском оптимального распределения грузов от поставщиков потребителям на сетевой модели [1-4, 8]. Такая задача, заданная транспортной таблицей (с объемами грузов у поставщиков и требуемыми объемами грузов потребителей) имеет стандартные методы решения, например, метод формирования опорных планов, метод потенциалов для поиска оптимального плана решения, другие аналитические методы [5-7, 9].

В данном исследовании такая классическая задача переводится в сетевую форму и решается по технологиям использования методов на конечном графе [10]. Именно такую интерпретацию можно отнести к некоторому виду геометрического представления решения. Причем в сетевом виде отличительно формируются и проверяются условия (требования) известных аналитических методов, в том числе и метода потенциалов.

Итак, в сетевом представлении транспортной задачи в виде графа принимаем:

• -    вершины - поставщиками с объемами производимых a i ед. ( i = 1, m ) грузов (со знаком «+») или потребителями с требуе-

• мыми объемами bj ед. (j = 1, n) грузов (со знаком «-»);

• -    ребра - путями перевозок с указанными над ними тарифами c j перевозок в стоимостном плане от i- ого поставщика j- ому потребителю.

При сетевом варианте решения транспортной задачи методом потенциалов должны выполняться следующие требования и ограничения:

• -    груз от поставщиков вывозится полностью, и все потребности удовлетворяются также полностью;

• -    количество ребер (стрелок) меньше количества вершин (поставщиков и потребителей) на единицу;

• -    нет замкнутых контуров цепи, и в каждой вершине графа есть входящие и выходящие ребра (стрелки);

• -    допускается добавление ребер графа для фиктивных поставщиков или потребителей (при необходимости) с нулевой стоимостью.

Определение оптимального плана перевозок транспортной задачи в сетевой форме рассмотрим на примере конкретного графа с числовыми значениями (условиями) на вершинах и ребрах графа, представленного на рисунке 1.

По графу видим, что в вершинах: А ₁ (I) и А ₂ (II) – поставщики, В ₁ (III), В ₂ (IV),

В ₃ (V) – потребители с указанными в них же соответствующими весами грузов.

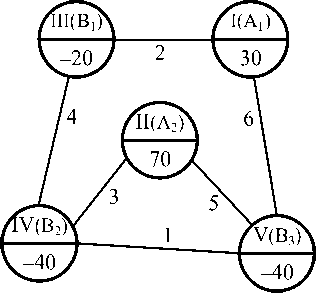
Рис. 1. Сетевой вид транспортной задачи

Заметим, что транспортная задача закрытая: суммарный груз поставщиков (30 ед. + 70 ед.) равен по абсолютной величине суммарным потребностям (40 ед. + 40 ед. + 20 ед.).

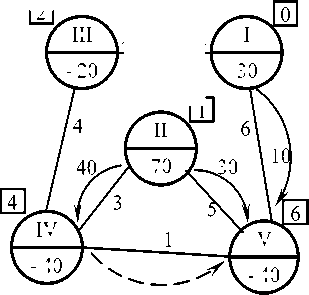
Первый опорный план в сетевом виде построен и представлен на рисунке 2, в котором перевозимые грузы с весами обозначены над выделенными стрелками.

III

I

–20

II

IV

V

–40

–40

Рис. 2. Первый опорный план

Для того чтобы проверить план на оптимальность, опишем и применим метод потенциалов для сетевой формы. Метод начинается с того, что одной из вершин (в нашем случае, вершине I (рис. 2)) задаем где ai, в - числа (потенциалы) каждой вершины графа.

Равенства (1) соответствуют поиску потенциалов для каждой базисной (заполненной) клетки задачи с условиями в виде транспортной таблицы. Число базисных клеток составляло бы m + n — 1, и (1) об- определенное значение потенциала (пусть 0). И далее определяем потенциалы других вершин сети (с учетом стрелок), используя стандартное правило метода:

a + в = cj, (1)

разовали бы систему из m + n уравнений с бесконечным множеством решений. Тогда поиск единственных значений потенциалов (единственного решения системы (1)) и подразумевает задание одного из значений потенциала, и при этом остальные значения потенциалов будут определяться однозначно.

В нашем случае сетевого вида задачи поступаем следующим образом: если стрелка выходит из вершины графа, то к потенциалу этой вершины добавляем (прибавляем) значение c этой стрелки, если же направление стрелки противоположно, то из потенциала вершины убираем (вычитаем) c .

Приведем наши расчеты потенциалов в соответствующих вершинах графа (они же для ребер без стрелок (в сетевом варианте метода потенциалов), что соответствует незаполненным клеткам транспортной таблицы задачи.

Для сетевого графа проверка неравенств (2) означает следующее: из большего потенциала вершины убирается (вычитается) меньший потенциал (другой связывающей вершины), и полученная разность убирается (вычитается) из показателя c тарифа, отвечающего ребру, связывающему вершины.

Приведем расчеты по неравенствам (2) для ребер графа без стрелок:

Δ 34 =4 – (4 – 2)=2,

Δ ₄₅ =1 – (6 – 4)= – 1.

Видим, что Δ ₄₅ отрицателен («отрицательная оценка»), значит, план пока не оптимален.

Нужно провести перераспределение грузов и получить новый опорный план. При этом в задаче, заданной транспортной таблицей, по методу потенциалов груз необходимо добавить в клетку с отрицательной оценкой.

В сетевом же виде такое добавление означает, что нужно «загрузить» ребро без стрелки с соответственной отрицательной оценкой и дорисовать к нему новую (пунктирную) стрелку, направленную от вершины с меньшим значением потенциала к вершине с большим значением. При указаны в квадратных рамках около вершин на рисунке 2):

– III: 0+2= 2 (стрелка выходит из I);

– V: 0+6= 6 (стрелка выходит из I);

– II: 6 – 5 = 1 (стрелка входит в V);

– IV: 1 +3 = 4 (стрелка выходит из II) .

Зная теперь потенциалы проверим полученный план на оптимальность, проверяя выполнение неравенств:

Δ ij = c ij - ( α i + β j ) ≥ 0                      (2)

этом образуется замкнутый контур из стрелок.

В нашем примере такое перераспределение грузов с добавлением новой пунктирной стрелки от вершины IV к вершине V (отрицательная оценка у Δ ₄₅ ) показано на рисунке 2.

При перераспределении грузов используем следующее правило:

– рассматриваются стрелки замкнутого контура с направлением, противоположным направлению новой стрелки;

– среди них находится стрелка с наименьшим тарифом ( х = min c _ij ) ;

– найденное значение х прибавляется к тарифам c _ij стрелок, имеющих то же направление, что и новая (пунктирная) стрелка, и вычитается из c _ij стрелок с противоположным направлением;

– стрелка, по которой выбрано число х удаляется, общее количество стрелок остается прежним.

В нашем примере имеем: х = min c _ij = 30, тогда тариф (стоимость) 30 добавляем от вершины II к вершине IV (30+40=70), прибавляется от вершины IV к вершине V (0+30=30), пунктирная стрелка становится сплошной. Тариф х, равный 30 убирается от II к V (30-30=0), поэтому соответствующая стрелка убирается.

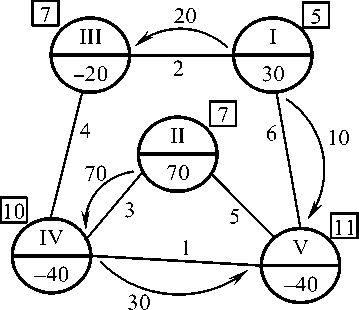
Рис. 3. Второй опорный план

Итоговый новый опорный план показан на рисунке 3. Проверим его на оптимальность. Для этого вычислили потенциалы с учетом (1), они выделены в квадратах рядом с вершинами графа (рис. 3) и проверили неравенства (2):     Δ ₃₄ =4 – (10 –

7)= 1, Δ ₂₅ = 5 – (11 – 7)= 1 . Итак, новый план – оптимален.

Определим транспортные расходы задачи с учетом полученного плана:

20 ⋅ 2+10 ⋅ 6+30 ⋅ 1+70 ⋅ 3= 340 д.е.

Значит, оптимальный план перевозок в сетевой форме представлен на графе ри- сунка 3, по которому затраты на перевозки составят 340 д.е.

Проведенное исследование на конкретном примере показывает возможность поиска решения транспортной задачи в сетевой форме. Перевод аналитических методов (поиска опорного плана, метода потенциалов) в сетевой формат решения подразумевает также проверку условий оптимальности полученных планов также в графическом виде. Причем такой формат имеет особенности в применении стандартных аналитических методов, формируя свои динамические правила их использования.