Алгоритм поэтапного уточнения проективного преобразования для совмещения изображений

Жёсткие ограничения, налагаемые на время обработки разноспектральных изображений в авиационных системах технического зрения (СТЗ), вынуждают искать быстрые алгоритмы решения задач в таких системах. Одной из наиболее сложных в комплексе задач, решаемых в бортовом вычислителе, является задача совме щения пары в общем случае разнородных изображений (телевизионное или тепловизионное, с одной стороны, и виртуальное изображение, построенное по цифровой карте местности, с другой). Корреляционные методы совмещения дают, как правило, гарантированный результат [1]. Однако из-за ошибок в навигационных параметрах летательного аппарата для пол учения этого результата требуется выполнить построение около 106 вирт уальных изображений под различными ракурсами, осуществить совмещение каждого из этих изображений с реальным изображением и получить оценку критериальной функции. Такой подход требует недопустимо больших затрат машинного времени, исключающих применение методов этой группы в реальных СТЗ.

Использование методов контурного анализа для компактного описания наблюдаемой сцены [2] и методов проективной геометрии [3] для совмещения пары изображений является обнадёживаю щей альтернативой корреляционным методам совмещения. Основные шаги такой технологии таковы:

• -    выделение контуров объектов на реальном изображении;

• -    аппроксимация контуров на реальном и виртуальном изображениях многоугольниками;

• -    выбор угло вых точек много угольников в качестве ключевых и установление соответствия между ними;

• -    построение проективного преобразования и совмещение изображений;

• -    оценка качества совмещения.

Предметом обсуждения в настоящей работе являются последние два этапа описанной технологии. Изображения, получаемые на борту воздушного судна от разноспектральных датчиков, как правило, со- держат проективные искажения. Они описываются дробно-линейными функциями, содержащими в общем случае 8 неизвестных параметров (в случае плоской гомографии) [3].

Проблема оценивания параметров проективного преобразования по опорным (ключевым) элементам рассматривалась многими авторами, в частности, в работах [4, 5]. В [4] предложена двухэтапная процедура формирования пространственного преобразования для совмещения изображений. В данной статье рассматривается аналогичная задача, для решения которой предлагается альтернативный алгоритм поэтапного уточнения проективного преобразования.

Поиск ключевых точек является наиболее важной задачей в методе совмещения изображений с помощью проективного преобразования. Далеко не всегда удается найти такие точки в автоматическом режиме. Технология получения множества пар ключевых точек в автоматическом режиме представлена в работе [6]. Но если даже найдено некоторое множество пар ключевых точек, то остаётся вопрос об их оптимальном использовании. Неудачный выбор ключевых точек может приводить к плохому и даже очень плохому качеству совмещения изображений. Один из широко применяемых методов автоматического выбора корректного набора точек – метод RANSAC [7].

1.    Технология и алгоритмы обработки изображений

Для учета проективных искажений можно использовать дробно-линейные преобразования [3]:

У =

h 11 x '+ h ₁₂ y '+ h ₁₃ h 31 x '+ h 32 y '+1 h 21 x '+ h 22 y '+ h 23 h ₃₁ x ‘+ h ₃₂ y ‘+ 1

или в матричной форме в однородных координатах

( % x )

" y

V % 7

^{( h 1} 1

^{h 21}

V h 31

h12 h13) (x ’' h 22 h 23 • у ‘ h32    1 J V 1 J

Матрица гомографии H =( h ij ) 3×3 в составе формулы (1) содержит 8 неизвестных параметров, для нахождения которых необходимо как минимум 4 пары ключевых точек на сопоставляемых изображениях. Формирование множества пар ключевых точек, с одной стороны, и выбор из этого множества оптимального набора точек, обеспечивающих корректное определение элементов матрицы гомографии, с другой стороны, – две основные задачи в проблеме совмещения изображений с помощью матрицы гомографии.

Для решения первой задачи предложено большое число методов (SURF, SIFT [9, 10], методы, основанные на идеях контурного анализа [6]). Первые два метода (SURF, SIFT) дают хорошие результаты при поиске ключевых точек на паре изображений, полученных с помощью однотипных датчиков, и неприемлемы для сопоставления разнородных изображений, особенно если последние представлены контурами основных объектов на подстилающей поверхности. Именно такие изображения приходится сопоставлять в авиационных СТЗ. Для поиска ключевых точек на контурных изображениях в [6] предложены методы, дающие достаточно хорошие результаты.

Для каждой пары ключевых точек Xi = (xi, yi)T и X'=(x', y') T, i = 1, k в соответствии с формулами (1) можно составить пару ура внений x ix'h3 1 + xiy'h32 + x i = x'h11 + y ' h12 + h13, У xh31 + У iyh32 + У i = xh21 + yh22 + h23 .

Система линейных алгебраических уравнений (СЛАУ) вида (3), преобразованная к стандартной форме записи СЛАУ, имеет следующий вид

AG h = B ,

где A – основная матрица    системы,

GH = (h11 h12 h13 h21 h22 h23 h31 h32)T -    векТоР- столбец подлежащих определению элементов матрицы гомографии, B = (x1 x2 x3 x4 y1 y2 y3 y4)T -вектор-столбец координат ключевых точек первого изображения, записанных в указанном порядке. Матрицу A и вектор-столбец B в составе (4) можно записать в блочной форме A =

O

Z

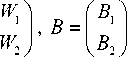
. Здесь

x ^y ' 1" x 2 у 2 ¹ x 3 ^y 3 1

I x 4 У 4 1 J

^O = ( ° ) 3 X 3

' - ^x 1 ^x ' - ^x 1 y ‘ ' - x 2 x 2 ^- x 2 У 2 ^- x . ^x 3 - x , ^y :

I- x4 x 4r - x 4 У 4 J f-y'x1' -yy1')

• ^- У 2 ^x 2 ^- У 2 У 2 /              /

• ^{- y} 3 x 3    ^{- y} 3 ^y 3

( ^- У 4 x 4 ^- У 4 У 4 J

СЛАУ (4) будет иметь единственное решение, если ранг её основной матрицы равен 8.

Выбор из множества k(k>>4) пар ключевых точек четырёх наилучших я вляется непростой задачей. Как показывают исследования, даже применение алгоритма RANSAC для ре шения этой задачи не всегда обеспечивает получение хоро шего результата [8]. Поэтому естественным представляется желание использовать всё множество пар ключевых точек для поиска матрицы гомографии. Однако в этом множестве могут быть пары либо с ложным соответствием, либо пары, в составе которых координаты одной точки в паре определены недостаточно точно. В этом случае предлагается использовать процедуру поэтапного уточнения матрицы гомографии, а именно:

– находить матрицу гомографии по всему множеству пар ключевых точек и выполнять совмещение изображений;

– оценивать качество совмещения изображений. Если совмещение неудовлетворительное, то находить пару (пары) ключевых точек, расстояние между образами которых оказалось наибольшим, и удалять их из множества пар ключевых точек;

– вновь находить матрицу гомографии по сокращённому множеству пар ключевых точек, выполнять совмещение изображений, оценивать качество совмещения и, возможно, удалять некоторые пары ключевых точек и т.д., пока не будет получено удовлетворительное совмещение изображений.

Описанная технология поиска матрицы гомографии, обеспечивающей наилучшее совмещение изображений по имеющемуся множеству пар ключевых точек, предполагает изменение алгоритма нахождения элементов матрицы гомографии. Если мы используем все k пар ключевых точек, то система (4) будет состоять из 2 k уравнений. Её решение с помощью любого численного алгоритма, не обладающего вычислительной устойчивостью (метод Гаусса и др.), может приводить к ошибочным результатам. Поэтому от СЛАУ вида (4) целесообразно перейти к нормальной СЛАУ:

( A T A ) G H = A T B .

Решать СЛАУ (5) целесообразно любым методом, предназначенным для решения систем с симметричной и положительно определённой основной матрицей (например, метод квадратного корня [11]).

Переход от системы (4) к нормальной СЛАУ (5) эквивалентен поиску преобразования H , минимизирующего сумму квадратов уклонений образов HX ′ точек X ′от соответствующих им точек X , т.е.

k

F ( G H ) = 2

i = 1

( x i ^-ф 1 ⁽ x i , ^x ' , y ') ) ² + ' _ч + ( У, -Ф 2 ( y, , x ' , У ) ) ² J

^ min, h ij

где ф1 = x'hn + y'h12 + h13 -xx'h31 - xiy'h32, ф2 = x'h21 + y'h22 + h23 - y,x'h31 + У У>32 •

В рамках стандартного метода наименьших квадратов из необходимого условия минимума [( d F ( G h ))/( d G h )] =0 функции F ( G h ) получаем систему уравнений (5).

Тогда СЛАУ (5) можно переписать в равносильной форме

A

Z Z

О v W1 TZ

O Z T Z W ₂ T Z

Z^TW ₁

Z^TW ₂

W^W1 + W2 W^i f    ZT B1

Z T B 2

_ч Wy B1 + W₂^TB ₂

• G h

2.    Экспериментальные исследования. Оценка качества совмещения

В процессе апробирования алгоритмов были выполнены эксперименты по совмещению пары изображений, полученных от однотипных датчиков (телевизионных), а также от датчиков разных типов (видео- и тепловизионный датчики). В первом случае выполнялось совмещение видеоизображений островов, полученных с борта воздушного судна с задержкой в несколько секунд. На рис. 1 приведен один из двух сопоставляемых контуров островов, полученный в результате предварительной обработки видеоизображения (обнаружение границ перепада яркости, замыкание контурных линий, аппроксимация замкнутых контуров многоугольниками, поиск ключевых точек и установление соответствия между ними). Знаком «звёздочка» с номерами указаны ключевые точки первого контура (18 точек). На горизонтальной и вертикальной осях приведена масштабная сетка, которая автоматически формируется средствами пакета MATLAB и характеризует размер изображений в пикселях.

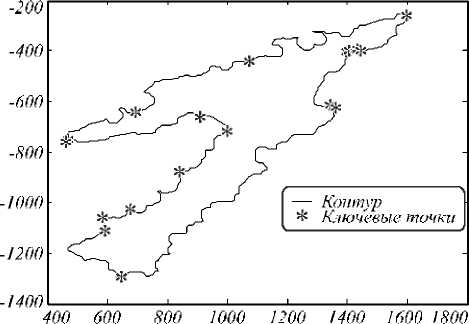
Рис. 1. Контуры острова с найденными на нём ключевыми точками

Аналогичный вид с точностью до проекти вных искажений , обусловленных разницей во времени между съёмками , и локальных изменений , возник ших на этапе морфологической обра ботки , имеет и второе изображение . Оно с целью экономии здесь не приводитс я .

Для нахождения наилучшего варианта приведения одного изображения к плоскости другого в работе [8] был выполнен полный перебор сочетаний из 18 точек по четыре точки. В итоге были построены 3060 матриц гомографии (3060 = C 14), выполнены совмещения изображений и в каждом случае оценено качество такого совмещения. Матрицы гомографии в этом ва- рианте находились в результате решения СЛАУ (4). На рис. 2 приведено лучшее из 3060 со вмещений кон- туров, найденное с помощью соответствую щей матрицы гомографии в процессе полного перебора ключевых точек. Ему отвечают пары точек: 6, 9, 14, 18 и матрица гомографии f 0,865       0,018     61,023'

0,045       0,910    40,303

(- 1,51 x 10 ^{- 5} - 2,06 x 10 ^{- 5}     1 J

Это совмещение в дальнейшем мы будем рассмат- ривать как эталонное.

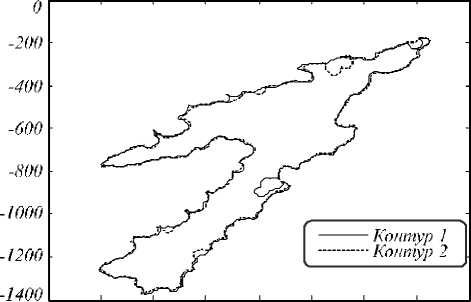
Рис. 2. Лучшее из 3060 совмещений

Для оценки качества совмещения изображений, представленных контурами основных объектов, была разработана специальная методика. Совме щение даже однородн ых изображений, но отли чаю щи хся временным сдвигом , невозможно осуществить идеально (пиксель в пиксель). Если же производится совме щение разнородн ых изображений, то их идеальное со вме щение невозможно в принципе из-за того, что на реальном изо бражении могут присут-ство вать контуры объектов, которых нет на цифровой карте местности (деревья, локал ьные изменения береговой линии и т.д.). Поэтом у даже при хорошем (на виз уальном уровне) со вме щении контур ов число совпа вши х пикселей двух изо бражений может быть относительно небольшим. Один из известных способов получения более адек ватных оценок качест ва совме щения конт ур ов заключает ся в применении специальной процедур ы утолщения тонки х линий контур ов. Однак о добиться аналогичного результата можно иначе, выполни в вычисления, имитирующие утолщение линий контуров.

Основная идея предлагаемого метода заключается в следующем. Изображение разбивается на квадратные блоки (клетки) определённого размера, например, 100×100 пикселей. Это даёт возможность получать не только интегральную оценку качества совмещения, но и локальные оценки в каждом из выделенных квадратных блоков. В каждой клетке для всех информативных (отличных от цвета фона) точек одного из изображений ищутся информативные точки друго го изображения, лежащие в некоторой квадратной окрестности размером (2k+1)×( 2k+1) с центром в обрабатываемой информативной точке. Как правило, k = 1 или k =2. Значение k = 1 равносильно утол щению тонкой линии в один пиксель первого контура до трёх пикселей, а k =2 – до пяти.

Скользящее окно выбранного размера (в рассматриваемом эксперименте 5×5) перемещается по строкам изображения. Как только информативная точка первого изображения попадает в центр этой окрестности, то ищутся и помечаются информативные пиксели второго изображения, попавшие в эту окрестность и не помеченные на предыдущих этапах. После того, как выполнено сканирование всего изображения, в каждом квадратном блоке подсчитывается число mi помеченных точек совмещаемого (второго) контура и находится отно шение этого числа к общем у числу информативных точек Mi первого контура, т.е. ai = mi/Mi. Коэффициент ai логично назвать показателем качества совмещения в i-м блоке изображения, а коэффициент a = (2mi /^Mi) - интегральным ii показателем качества совмещения всего контура.

Интегральные оценки качества совмещения контуров для 9 луч ши х наборов из 4 пар ключевых точек приведены в таблице. Данные результаты получены при разбиении исходного изображения на блоки размером 100×100 пикселей и значении параметра k =2. Исходн ые изображения островов имеют размер 1700×1500 пикселей.

Табл. 1. Показатели качества совмещения

№ п/п	Номер в наборе из 3060 групп	Набор точек (рис. 1)	Показатель a качества совмещения
1	1959	4, 9, 12, 17	0,824
2	1960	4, 9, 12, 18	0,805
3	2017	4, 11, 14, 17	0,828
4	2459	6, 9, 11, 17	0,815
5	2460	6, 9, 11, 18	0,816
6	2465	6, 9, 12, 17	0,835
7	2474	6, 9, 14, 17	0,843
8	2475	6, 9, 14, 18	0,848
9	2538	6, 12, 11, 17	0,812

Приведённые в табл. 1. результаты достаточно интересны. Визуальный анализ рис. 1 позволяет предположить, что наилучшими должны были бы быть наборы ключевых точек 3, 10, 15 или 16, и 17 или 18. Указанные наборы также дают достаточно высокое качество совмещения, например, для набора 3, 10, 15, 18 значение показателя a качества совмещения равно 0,795. Однако приведённые в таблице оценки качества совмещения выше (все больше 0,8). Для автоматизации процесса поиска наилучшего набора из 4 пар точек нужна специальная технология отбора таких точек. Второй вывод этого этапа исследования – «хоро ший» набор из 4 точек на контуре не единственен, важно лишь правильно его найти.

На следующем этапе исследований поиск оптимальной матрицы гомографии выполнялся сразу по всему множеству пар ключевых точек с последующим удалением из него «плохих» точек и вычислением новой матрицы гомографии. Для сравнения получаемых совмещений использовались показатель качества совмещения a, матрица гомографии и евклидово расстояние р(X,,HX’}, i = 1,к между ключевыми точками одного контура и отвечающими им образами точек другого контура. Результат совмещения контуров островов с использованием всех 18 точек представлен на рис. 3. Как визуальный анализ, так и анализ значений перечисленных показателей свидетельствуют о том, что данное совмещение далеко от идеального (a = 0,176). Причина данного явления заключается в том, что в наборе из 18 пар точек есть «неудачные».

Среднее значение расстояния в евклидовой метрике между ключевыми точками первого контура и отвечающими им образами точек второго контура k

( R h = Т 2 р ( X , HX ’ k i = 1

) ) по всем 18 точкам равно

• 38,59.    Тогда как для эталонного совмещения оно равно 18,41. Свидетельством неудачного совме щения является и матрица гомографии

' 0,211 - 0,206 429,72 '

• - 0,144 0,320 301,69

(0,0003 -0,0003     1 J для данного варианта в сравнении с матрицей гомографии (7) эталонного совмещения.

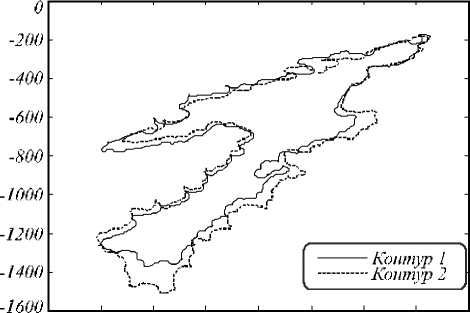
200 400 600 800 1000 1200 1400 1600 1800

Рис. 3. Совмещение контуров с помощью матрицы гомографии, найденной по всем 18 ключевым точкам

Анализ расстояний р ( X i , X ' ) , i = 1,18 в евклидовой метрике между соответствую щими точками первого и второго контуро в показал, что наибольшее уклонение наблюдается на паре точек под номером 1 ( р ( X 1 , X ’ ) = 192,87 ) (табл. 2).

Удалим пару точек под номером 1 из набора и выполним процедуру совме щения по набору из 17 точек. Результат этого совмещения приведён на рис. 4.

Уже визуальный анализ говорит о том, что положение изменилось кардинально – совмещение близко к идеальному. Показатель качества в данном случае a = 0,730 .

Табл. 2. Расстояния в пикселях между ключевыми точками первого контура и образами соответствующих им точек второго контура

№ пары точек	Р асстояние между точками	№ пары точек	Расстояние между точками
1	192,87	10	113,95
2	48,79	11	78,56
3	88,23	12	80,05
4	61,74	13	58,83
5	64,35	14	38,07
6	51,92	15	20,09
7	67,23	16	32,01
8	22,47	17	53,85
9	29,61	18	51,47

о

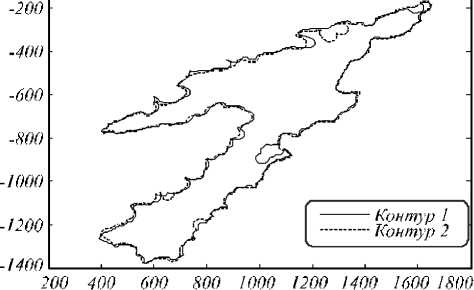
Рис. 4. Совмещение контуров по 17 ключевым точкам (без пары точек под номером 1)

Это заключение подтверждается и объективными характеристиками: значение R_H = 18, 95 близко к оптимальному значению R_H = 18,41 , матрица гомографии также несущественно отличается от матрицы (7)

' 0,941      0,052    21,93 "

0,047      1,018    17,86

_ч 8,32 х 10 ^{- 6} 3,74 х 10 ^{- 5}     1 _?

Теперь можно сформулировать критерии сокращения множества пар ключевых точек. Мы должны исходить из того, что сокращение должно приводить либо к улучшению качества совмещения, либо не должно существенно ухудшать его. Первое требование должно достигаться при удалении «плохих» ключевых точек. Как правило, это пары точек, в которых расстояние ρ ( X_i , X_i ′ ) между точками одного контура и отвечающими им точками другого контура существенно больше среднего расстояния по всему множеству ключевых точек. Второй критерий отсеивания – выбор из нескольких близко расположенных ключевых точек одной.

По первому критерию, как это следует из табл. 2, должна быть удалена пара точек под номером 1 и, быть может, под номером 10. Выше было показано, что удаление пары точек под номером 1 кардинально меняет качество совмещения.

Анализ расстояний между соседними точками на одном и втором контурах говорит о том, что некото- рые из них расположены близко друг к другу и, значит, в каждой такой группе можно оставить только одну точку. Такие группы в на шем примере образуют, например, подмножества{4, 5, 6, 7}, {8, 9}, {17, 18}. Сократим каждое подмножество до одной точки: {4,5,6,7}→{4}, {8,9}→{8}, {17, 18}→{17}.

Выполним теперь поиск матрицы гомографии с удалённой парой под номером 1 и удалёнными парами под номерами 5, 6, 7, 9, 18. Показатели качества совмещения при этом ухудшились, но, заметим, совсем несущественно: R_H = 19, 21, α = 0,768 , матрица гомографии

" 0,943 0,048 26,65 "

0,044 1,022 20,26

ч1,13х10-5 3,99 х10-5 1 , незначительно отличается от матрицы (8). Альтернативная и достаточно распространённая методика определения «оптимальных» значений параметров проективного преобразования заключается в использовании метода RANSAC. Для сопоставления предлагаемого авторами подхода с результатами, которые даёт RANSAC, было проведено микроисследование. Оно заключалось в многократном (30 раз) запуске RANSAC на рассматриваемом множестве из 18 пар ключевых точек, вычислении с его помощью матрицы гомографии, выполнении совмещения и оценки качества совмещения. Результаты таковы: всего получено 9 различных матриц гомографии и соответственно вариантов совмещения, один из них оказался совершенно некачественным и повторился 6 раз в 30 экспериментах (рис. 5) (α = 0,056), 4 различных варианта матриц гомографии с невысоким качеством совмещения (рис. 6) (α = 0,214–0,368) и 4 варианта матриц гомографии с хорошим качеством совмещения (α = 0,801), причём хорошие результаты совмещения были получены только в 9 из 30 запусков RANSAC (применялась версия RANSAC, реализуемая функцией estimateGeometricTransform из пакета MATLAB R2014a).

Основные выводы данного этапа:

• -    поиск матрицы гомографии необязательно осуществлять строго по 4 ключевым точкам, возможен расчёт по произвольному количеству ключевых точек;

• -    соседние точки контуров, расстояние между которыми невелико, можно заменить одной из них, без существенной потери качества;

• -    если в исходном наборе пар ключевых точек есть пара, расстояние между которой существенно больше среднего по множеству, то такая точка должна быть удалена из набора.

Отметим, что близкие к нулю значения элементов h31, h32 в третьей строке найденных матриц гомографии во всех экспериментах говорят фактически об отсутствии проективных искажений между сравниваемыми изображениями и, соответственно, о возможности упрощения алгоритма. Однако предлагаемый алгоритм рассчитан на использование в реальных авиационных СТЗ и должен учитывать возможное нали- чие проективных искажений между сравниваемыми изображениями.

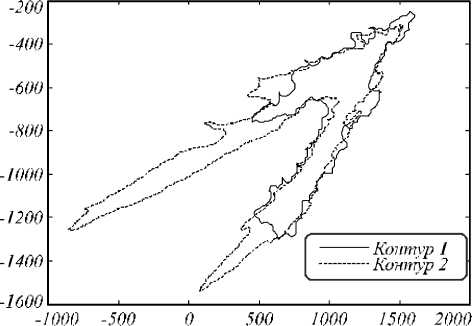
Рис. 5. Пример неудачного результата RANSAC

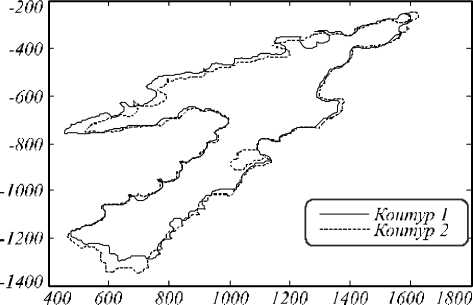
Рис. 6. Пример результата RANSAC с невысоким качеством совмещения

Приведём пример совмещения телевизионного и тепловизионного изображений. Телевизионная и тепловизионная камеры жёстко закреплены на некотором расстоянии друг от друга на борту воздушного судна. Параметры камер: телевизионная – горизонтальный угол обзора – 41°, вертикальный – 30,7°, тепловизионная система имеет поле зрения 20°×16° по горизонтали и вертикали соответственно. Поскольку положение камер в процессе полета не меняется, то естественно ожидать, что матрица гомографии для данного фиксированного положения камер в процессе полета также не будет меняться. Значит, можно выбрать любую пару чётких изображений подстилающей поверхности, содержащей чётко выделенные (на исходном изображении) контуры объектов, отметить на них по 4 пары ключевых точек, пусть даже вручную, и вычислить матрицу гомографии. Проведённые эксперименты подтвердили это предположение. Корректно рассчитанная один раз матрица гомографии обеспечивала хорошее совмещение телевизионного и тепловизионного изображений на протяжении всего полёта.

В качестве иллюстрации на рис. 7 приведены исходные изображения одного участка подстилающей поверхности (рис. 7а – тепловизионное изображение подстилающей поверхности, рис. 7б – чёрно-белое телевизионное изображение, рис. 7в – результат совмещения телевизионного и тепловизионного изображе- ний подстилающей поверхности), полученные с этих камер в некоторый момент времени, результат их совмещения с помощью найденной матрицы гомографии

' 0,5    0,03

- 0,02 0,55 0      0

¹⁵9,1³ )

174,64

¹ J

.

Также было выполнено совмещение других кадров из видеоряда на протяжении всего полёта с помощью найденной матрицы гомографии. Результат совмещения во всех случаях хороший.

а)

б)

в)

Рис. 7. Совмещение изображений подстилающей поверхности

Заключение

В статье предложена технология совмещения изображений в условиях неопределённости относительно качества сформированного множества ключевых точек. Технология основана на обнаружении и поэтапном отсеивании неудачных пар ключевых точек. Приведена методика получения локальных и интегральных оценок качества совмещения изображений. Приводятся результаты совмещения изображений подстилающей поверхности с применением предлагаемого подхода.