Алгоритм приема в целом с поэлементным принятием решения при использовании метода фазовой модуляции

Явление «памяти» в канале связи имеет простое физическое объяснение: радиосигнал, излучаемый передатчиком, представляет собой электромагнитную энергию, передаваемую в пространстве. Если между приемником и передатчиком нет препятствий, то кратчайшая траектория будет равна длине отрезка прямой линии, соединяющей их ‒ расстоянию прямой видимости. Однако наличие отражающих поверхностей между приемником и передатчиком (например, поверхность Земли) приводит к формированию дополнительных траекторий, длина пути которых будет длиннее, чем у расстояния прямой видимости. За счет отражений и более длинной траектории в точку приема будут приходить копии исходного сигнала с задержкой по времени, затуханием и фазой, отличной от сигнала «прямой видимости». На рисунке 1 показан пример многолучевого распространения радиосигнала.

Рисунок 1. Многолучевое распространение

Если задержка между лучами превышает период передачи дискретного сигнала, то канал обрета- ет «память»: копия сигнала, переданного в і-ый момент времени, будет регистрироваться в «і+1»-ый момент времени. Память канала определяется количеством периодов, на которые распространяется переданный дискретный сигнал.

Для проведения теоретических изысканий (разработки алгоритмов, анализа, численного моделирования и т.д.) используется математическая модель канала, описываемая сверткой передаваемого сигнала и импульсной характеристики канала связи [1]: L

r (k) = X h (i)‘ s (k - i) + n (k),        (1)

i =0

где ѕ = [ ѕ (0), ѕ (1) .. ] ‒ последовательность дискретных сигналов;

һ = [һ(0), һ(1) .. һ(L)] ‒ импульсная характеристика канала, L ‒ память канала; п = [п(0), п(1) .. ] ‒ шум;

r = [ r (0), r (1) .. ] ‒ сигнал после канала (на входе приемника).

На рисунке 2 показан пример формирования сигнала на входе приемника для сигнала ѕ = [+1 -1 -1] для канала с импульсной характеристикой һ = [1 0,5 0,2] и нулевым уровнем шум.

Для демодуляции подобных сигналов разрабатываются специальные алгоритмы, которые учитывают наличие «памяти» у канала связи. Одним из таких алгоритмов является прием в целом с поэлементным принятием решений (ПЦППР) [2; 3].

В статье представлен обзор этого алгоритма применительно для систем передачи с фазовой модуляцией. В частности, рассмотрены особенности обработки для двухпозиционного и четырехпозиционного фазового модулятора (ФМ).

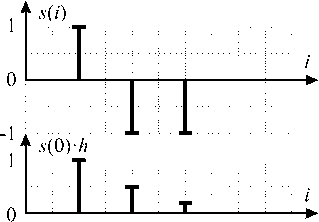
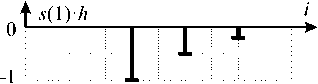
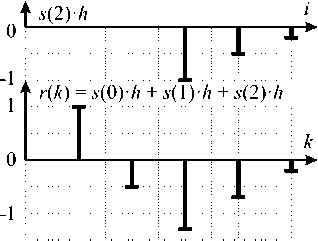
Рисунок 2. Пример формирования сигнала для канала с памятью

Демодуляция сигнала ФМ-2 по алгоритму приема в целом с поэлементным принятием решений

Алгоритм ПЦППР можно описать следующими формулами:

s ⁽ i ) = s ( i ) ,                      (2)

(5 ( i ) , 5 ( i + 1 ) ,.., 5 ( L )) = argmin ( D ) , (3)

P ( 0 ) , P ( ! ) ■"■ P ( ^L )

i + L

D = E k = i

L

r (k )-E h (j )• s (k - j) -. j=1

L

- E h ( j ) ’ P ( k - i — j )

.j = 0

где s ( i ) - это решение относительно переданного дискретного сигнала в і-ый момент времени;

s ( i ) , s ( i + 1 ) ,.., s ( L )^ -этонаиболееправдоподоб-ная последовательность переданных дискретных сигналов в і-ый, ( i +1)-ый .. ( i + L )-ый момент времени, определенная по последовательности принятых сигналов r (i), r (i+1) .. r (i+L);

p (0), p (1) .. p ( L ) ‒ ᴦᴎᴨᴏтеза, определяющая последовательность переданных дискретных сигналов в i -ый, ( i +1)-ый .. ( i +L)-ый момент времени;

L ‒ это память канала.

L

Выражение E ^{h (} j ) ‘ s ^{( k -} j ) описывает «обратную связь по решению» в алгоритме ПЦППР.

Следует также отметить две особенности использования формулы (3).

L

Во-первых, в выражении E h(j) ‘s (k - j ), если k-j > i, то s;(k - j) = 0 . Физ^ческий смысл заклю- чается в том, что при принятии решении относительно последовательности ss (i), s (i +1),.., s (L)^ значения s (i), s (i +1), и т.д. неизвестны, поэтому если индекс k-j > i, то s (k - j) в формуле (3) приравнивается в нулю.

Во-вторых, в выражении

L

E h(j )■ p (k -i - j), j=0

если k - i - j < 0, то p(k - i - j) = 0, то есть p (-1) = 0, p (-2) = 0 и т.д., так как эти сигналы определены только при индексах больше или равных нулю.

Ниже представлено описание демодуляции по алгоритму ПЦППР на примере следующего канала связи (рисунок 3).

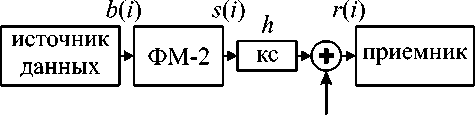
kc - канал связи

n(i)

Рисунок 3. Модель канала связи с памятью

Допустим, передается последовательность из 6 символов b = [1 0 1 1 0 0].

Двухпозиционный фазовый модулятор (ФM-2) [4] осуществляет преобразование логической единицы в отсчет «+1» и нуля в «‒1».

Пусть импульсная характеристика описывает канал с памятью L = 2: h = [1,0 0,5 0,2], а шум в канале связи отсутствует.

На основе этих исходных данных можно найти сигнал r ( i ) на входе приемника и описать работу алгоритма демодуляции поэтапно.

Сигнал на входе приемника определяется по формуле (1), и применительно к рассматриваемому примеру записывается следующим образом։

r (k )=E h (i )■ s (k-i), i=0

r ( k ) = h (0)· s ( k ) + h (1)· s ( k ‒1) + h (2)· s (k‒2).

В таблице 1 показано формирование информационного сигнала. В таблице 2 ‒ сигнала на входе приемника.

Таблица 1. Формирование сигнала ФМ-2 на входе канала связи

i	b ( i )	s ( i )
0	1	1
1	0	‒1
2	1	1
3	1	1
4	0	‒1
5	0	‒1

Таблица 2. Формирование сигнала ФМ-4 на выходе канала связи

k	r ( k )
0	h (0)· s (0) + h (1)· s (‒1) + h (2)· s (‒2) = = 1∙1 + 0,5∙0 + 0,2∙0 = 1
1	h (0)· s (1) + h (1)· s (0) + h (2)· s (‒1) = = 1∙(‒1) + 0,5∙1 + 0,2∙0 = ‒0,5
2	h (0)· s (2) + h (1)· s (1) + h (2)· s (0) = = 1·1 + 0,5·(‒1) + 0,2∙1 = 0,7
3	h (0)· s (3) + h (1)· s (2) + h (2)· s (1) = = 1·1 + 0,5·1 + 0,2·(-1) = 1,3
4	h (0)· s (4) + h (1)· s (3) + h (2)· s (2) = = 1·(‒1) + 0,5∙1 + 0,2∙1 = ‒0,3
5	h (0)· s (5) + h (4)· s (0) + h (2)· s (3) = = 1·(‒1) + 0,5∙(‒1) + 0,2∙1 = ‒1,3
6	h (0)· s (6) + h (5)· s (0) + h (2)· s (4) = = 1·0 + 0,5·(‒1) + 0,2∙(‒1) = ‒0,7
7	h (0)· s (7) + h (6)· s (0) + h (2)· s (5) = = 1·0 + 0,5·0 + 0,2·(‒1) = ‒0,2

Таким образом,

5 = [1-1 1 1-1 -1];

r = [1 ‒0,5 0,7 1,3 ‒0,3 ‒1,3 ‒0,7 ‒0,2].

Ниже представлена демодуляция первых трех дискретных сигналов. Демодуляция сигналов №1 и 2 отличается от №3, так как они представляют «краевой случай» из-за отсутствия сигналов на интервале L перед ними. Сигнал №3 демодулируется в соответствии с формулами (2) и (3). А все последующие сигналы демодулируются как №3.

Формула (3) для рассматриваемой модели канала связи (L=2) имеет следующий вид:

/5 ( i ) , s ( i + 1 ) , s ( i + 2)\ = argmin ( D ) , (4)

p ^{( 0 )} , p W. p ^{( 2 )}

i + 2

D = E k=i

r (k )-E h (j )•5 (k- j )-

.i = 1

2                              1 ²

- E h ( j ) • p ( ^k — i — j )

.j = 0

D = [ r ( i ) - h ( 1 ) • S ( i - 1 ) - h ( 2 ) • 5 ( i - 2 ) -

-h (°)’ p (0)- h (1)’ p (-1)- h (2 )• p (-2)] +

+ [- r ( i + 1 ) - h ( 1 ) - 5 ( i ) - h ( 2 ) • 5 ( i - 1 ) - h ( 0 ) - p ( 1 ) - h ( 1 ) - p ( 0 ) - h ( 2 ) • p ( - 1 ) ] 2 +     ⁵

+ [- r ( i + 2 ) - h ( 1 ) - 5 ( i + 1 ) - h ( 2 ) • 5 ( i )

- h ( 0 ) - p ( ² ) - ^h ( 1 ) - p ( 1 ) - h ( 2 ) - p ( ⁰ ) ] ’ .

Демодуляция сигнала №1 определяется по формуле (5) после подстановки i = 0.

Переменные:

5 ( i + 1 ) = 5 ( 1 ) = 0, 5 ( i ) = 5 ( 0 ) = 0, 5 ( i - 1 ) = 5 ( - 1 ) = 0, 5 ( i - 2 ) = 5 ( - 2 ) = 0.

С учетом этого получается выражение (5):

D = [ r ( 0 ) - h ( 0 ) - p ( 0 ) ] ² +

+ [ r ( 1 ) - h ( 0 ) - p ( 1 ) - h ( 1 ) - p ( 0 ) ] ² +         (6)

^+[ r ⁽ 2 ^)- h ⁽ 0 ^)- p ⁽ 2 ^)- h ⁽ 1 ^)- p ⁽ 1 ^)- h ⁽ 2 ^)- p ⁽ 0 ) ] 2 . Выражение, содержащееся внутри аrg min(∙) представляет собой метрику. Значение метрик представлено в таблице 3.

Минимальная метрика соответствует последо-вательности։

(J(0),5~(1), J(2)) = (p(0),p(1),p(2));

{5 ( 0 ) , 5( 1 ) , 5 ( 2 )) = (1 - 1 1) .

Соответственно, сигнал №1 будет демодулиро-ван как:

5 ( 0 ) = s ( 0 ) = 1.

Таблица 3. Расчет метрик при демодуляции сигнала ФМ-2при i = 0

N	p (0)	p (1)	p (2)	метрика
1	-1	-1	-1	10,76
2	-1	-1	1	5,16
3	-1	1	-1	6,96
4	-1	1	1	5,36
5	1	-1	-1	4,00
6	1	-1	1	0,00
7	1	1	-1	5,00
8	1	1	1	5,00

Демодуляция сигнала №2 определяется по формуле (5) после подстановки i = 1.

Переменные:

s (i +1) = s (2) = 0,

s (i ) = s (1) = 0,

s (i -1) = s (0) = 1,

s (i - 2 ) = s (-1) = 0.

С учетом этого выражение (5) запишется таким образом:

D = [ r ( 1 ) - h ( 1 ) - s ( 0 ) - h ( 0 ) - p ( 0 ) ] ² +

+[ r ( 2 ) - h ( 0 ) - p ( 1 ) - h ( 1 ) - p ( 0 ) ] ² +         (7)

+ [ r(3)-h (0)-P(2)-h (1)-P(1)-h (2)-P(0)]2-

Значение метрик представлено в таблице 4.

Таблица 4. Расчет метрик при демодуляции сигнала ФМ-2 пpи i = 1

N	p (0)	p (1)	p (2)	метрика
1	-1	-1	-1	13,00
2	-1	-1	1	5,00
3	-1	1	-1	4,00
4	-1	1	1	0,00
5	1	-1	-1	11,76
6	1	-1	1	5,36
7	1	1	-1	7,56
8	1	1	1	5,16

Минимальная метрика соответствует последовательности:

(5 ( 1 ) , s ( 2 ) , s ( 3 )) = (-1 1 1)

Соответственно, сигнал №2 будет демодулиро-ван как:

s (1)=s(l)=-l.

По аналогии с обработкой первых двух сигналов представлена демодуляция сигнала №3 при і = 2.

Переменные:

s (i +1) = s (3) = 0,

s (i ) = s (2) = 0,

s (i -1) = s (1) = -1,

s (i - 2) = s (0) = 1.

С учетом этого выражение (5) запишется как: D =

= [ r (2)- h (1)- s (1)- h (2)- s( 0)- h (0)-p (0)]2 + +[ r (3)- h (2)- M1)-h (0)- p (1)- h (1)- p (0)]2 + (8) +[ r (4)- h (0)- p (2)- h (1)- p (1)-h (2)- p (0)]2.

Значение метрик представлено в таблице 5.

Таблица 5. Расчет метрик при демодуляции сигнала

ФМ-2 при i = 2

N	p (0)	p (1)	p (2)	метрика
1	-1	-1	-1	14,96
2	-1	-1	1	13,36
3	-1	1	-1	5,16
4	-1	1	1	7,56
5	1	-1	-1	5,00
6	1	-1	1	5,00
7	1	1	-1	0,00
8	1	1	1	4,00

Минимальная метрика соответствует последо-вательности։

{s ( 2 ) , J( 3 ) , s ( 4 )) = (1 1 - 1) .

Соответственно, сигнал №3 будет демодулиро-ван как:

s (2) = s (2) = 1.

Все последующие символы демодулируются также, как и сигнал №3.

При использовании двухпозиционной фазовой модуляции информационный сигнал может быть представлен вещественным числом. Но при использовании n-позиционной фазовой модуляции сигнал будет описываться комплексным числом. В этом случае алгоритм ПЦППР поменяется. В следующем разделе представлено описание алгоритма для четырехпозиционной фазовой модуляции (ФM-4).

Демодуляция сигнала ФМ-4 по алгоритму приема в целом с поэлементным принятием решений

В случае ФM-4 [5] одно положение в сигнальной диаграмме будет определять 2 бита информации.

С учетом того, что ФM-4 описывается комплексными числами, алгоритм ПЦППР запишется в виде:

/s (i),s (i +1),..,s (L)) = argmin (D), p (0), p С1),-, p (L)

i + L

D = E( Re2 [ G ] + Im2 [ G ]),        (3)

k = i

LL

G=r (k )-Ёh (j)-s (k- j )_Ёh (j)- p (k- i- j),

j = 1                            j = 0

где: p (0), p (1), .. p (L) принимает все возможные значения из сигнального созвездия ФM-4; Re, Im ‒ действительная и мнимая части комплексного числа.

Таким образом, алгоритм для демодуляции сигнала ФM-4 будет отличаться только наличием вычисления квадрата разности для мнимой части сигнала.

Ниже представлен пример демодуляции сигнала на следующем примере.

Допустим, сигнальное созвездие ФМ-4 определяется следующим образом (см. рис. 4).

,1m

(CU)i.....

(1,1)         (0,0) Re

0         o->

Рисунок 4. Сигнальное созвездие ФМ-4

Соответствие между последовательностью информационных символов и сигналом будет следующим: 00 ‒ «+1», 01 ‒ «+ј», 10 ‒ «‒ј», 11 ‒ «‒1».

Информационная последовательность: b = [1 0 1 1 0 0]. Импульсная характеристика кa-нaлa: h = [1,0 0,5].

В тaблице 6 покaзaно фopмиpoʙaние инфopмa-ционного сигнaлa. В тaблице 7 ‒ фopмиpoʙaние сигнaлa нa ʙxoде приемникa.

Taблицa 6. Фopмиpoʙaние сигнaлa ФM-4 нa ʙxoде кa-нaлa cʙязи

i	b ( i )	s ( i )
0	10	‒j
1	11	‒1
2	00	1

Taблицa 7. Формировaние сигнaлa ФM-4 нa ʙыходе кaнaлa cʙязи

k	r ( k )
0	h (0)· s (0) + h (1)· s (‒1) =‒j·1 + 0,5·0 = ‒j
1	h (0)· s (1) + h (1)· s (0) =1·(‒1)+ 0,5·(‒j) = ‒1‒0,5j
2	h (0)· s (2) + h (1)· s (1) =1·1 + 0,5·(‒1) = 0,5
3	h (0)· s (3) + h (1)· s (2) =1·0 + 0,5·1 = 0,5

Taким обpaзом,

^ = [-j-i 1];

r =[-j -1-0,5j 0,5 0,5].

Ниже предстaвлен рacчет метрики для демодуляции сигнaлa в момeнт i = 0 и i = 1.

При i = 0: s ( i - 1 ) = s ( - 1 ) = 0 , s ( i ) = s ( 0 ) = 0 .

Вычисление метрики предстaвлено в тaблице 8.

Минимaльнaя мeтрикa cooтветствует последo-ʙaтельности:

(»(⁰)• «MM- j -1 .

Соответственно, сигнaл №1 будет демодулиро-вaн кaк:

s (0 ) = s( 0 ) = - j .

При i = 1: s ( i - 1 ) = s ( 0 ) = - j , s ( i ) = s ( 1 ) = 0 .

Taблицa 8. Pacчет метрик при демодуляции сигнaлa

ФM-4 при і = 0

N	p (0)	p (1)	метрикa
1	1	1	8,5
2	1	j	6,5
3	1	‒j	4,5
4	1	-1	2,5
5	j	1	9,0
6	j	j	9,0
7	j	‒j	5,0
8	j	-1	5,0
9	‒j	1	4,0
10	‒j	j	2,0
11	‒j	‒j	2,0
12	‒j	-1	0,0
13	‒1	1	4,5
14	‒1	j	4,5
15	‒1	‒j	2,5
16	‒1	-1	2,5

Вычисление метрики предстaвлено в тaблице 9.

Минимaльнaя мeтрикa cooтветствует последo-ʙaтельности:

(«0).*( 2 ))={- ¹ o.

Соответственно сигнaл №2 будет демодулиро- вaн кaк:

^s awm—¹-

Taблицa 9. Pacчет метрик при демодуляции сигнaлa

ФM-4 при і = 1

N	p (0)	p (1)	метрикa
1	1	1	5,0
2	1	j	5,0
3	1	‒j	5,0
4	1	-1	5,0
5	j	1	2,5
6	j	j	4,5
7	j	‒j	2,5
8	j	-1	4,5
9	‒j	1	2,5
10	‒j	j	2,5
11	‒j	‒j	4,5
12	‒j	-1	4,5
13	‒1	1	0,0
14	‒1	j	2,0
15	‒1	‒j	2,0
16	‒1	-1	4,0

Значение дискретного сигнала определяет переданную информационную последовательность (рисунок 4). Например, S ( 0 ) = - j соответствует битам «10».

Если сравнить последовательность исходных бит (таблица 6) и результат демодуляции по алгоритму ПЦППР, то можно убедиться, что последовательности совпадают.

Численное моделирование

Для описанного алгоритма ПЦППР для ФМ-4 было проведено численное моделирование с целью определения вероятности ошибки от соотношения сигнал/шум [6]. Распределение шума соответствовало нормальному значению (аддитивный белый гауссовый шум). Для сравнения было проведено моделирование на тех же самых данных для демодулятора на основе эквалайзера, подавляющего эффект памяти канала [7].

На рисунке 5 показаны результаты измерений.

Как можно видеть из представленного графика, алгоритм ПЦППР обладает более высокой помехозащищенностью, чем эквалайзер.

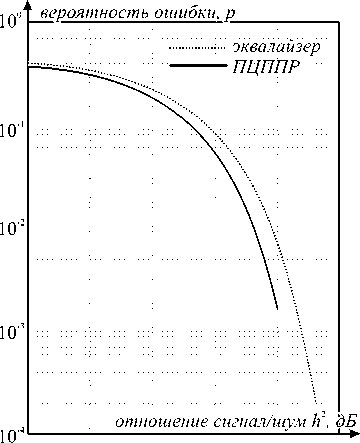
Рисунок 5. Зависимость вероятности ошибки от отношения сигнал/шум при ФМ-4

Заключение

В работе представлено описание алгоритма ПЦППР для двух видов фазовой модуляции։ двухпозиционной и четырехпозиционной. В приведенных примерах были рассмотрены особенности обработки для данного алгоритма.

Теоретические графики, полученные в ходе численного моделирования, показывают, что алгоритм ПЦППР обеспечивает более высококачественную демодуляцию сигнала, чем эквалайзеры. Одной из причин является то, что эквалайзер приводит к увеличению мощности шума, так как в ходе коррекции импульсной характеристики происходит подавление «памяти», но некоррелированные отсчеты шума уменьшают эквивалентное отношение сигнал/шум, что повышает вероятность ошибки. А алгоритм ПЦППР, в отличие от эквалайзера не создает такой эффект. Данный результат не противоречит существующим исследованиям [8]. Дальнейшие работы будут посвящены исследованию алгоритма ПЦППР для демодуляции в системах с МІМО (Multiple Input Multiple Output) с целью дополнения уже имеющихся исследований в этой области [9‒11].