Алгоритм радиуса окружности точки скрещивания ножей при двухстороннем исполнении гарнитуры

При размоле волокнистых полуфабрикатов в дисковых мельницах с традиционным (двухсторонним) исполнением [1] рисунка кольцевых размалывающих ножевых поверхностей (сцентрированных и сопряжённых через регулируемый зазор) вращающегося диска ротора и неподвижного диска статора прямолинейные режущие кромки их ножей:

• -    расположены с противоположных сторон относительно центра дисков;

• -    контактируют в точке скрещивания.

Расстояние от центра дисков до произвольной точки скрещивания является радиусом проходящей через неё окружности.

При исследовании процесса размола необходимо знание алгоритма данного радиуса. Известно [1], что алгоритм такого радиуса:

• -    зависит от угла скрещивания;

• -    раскрывает особенности и характер сопряжения режущих кромок ножей ротора и статора;

• -    несёт информацию, достаточную для постановки ряда промежуточных задач, решение которых позволит получить точный ответ относительно эффективности работы режущих кромок ножей ротора и статора.

По результатам анализа поисковой информации [13], касающейся методов определения известного алгоритма, был установлен факт его трансцендентности (неопределённости). Методы её устранения не обнаружены. Представляется, что для этого необходимо: графоаналитическое исследование, математически обоснованное корректирование, оперирование только входными геометрическими параметрами.

Можно предположить, что выполнение этих требований и условий позволит вывести аналитические зависимости полезной части длины режущих кромок ножей гарнитуры дисковых мельниц [1].

Материалы и методы исследования

На рисунке изображён общий случай фронтальной проекции кольцевой размалывающей поверхности сопряжения дисков ротора и статора. Для лучшего понимания режущая кромка 4 единичного ножа ротора, пересекающаяся с входной окружной кромкой 6 и режущей кромкой 5 ( AB^C ) единичного ножа статора, изображена в двух положениях:

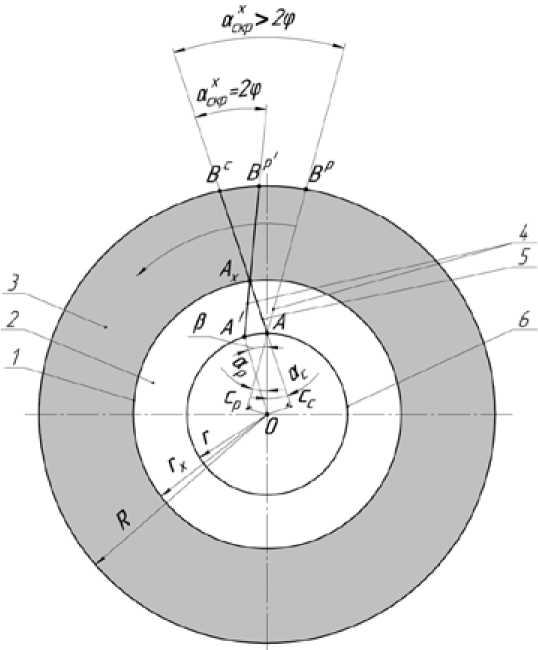
Рис. Кольцевая размалывающая поверхность сопряжения дисков ротора и статора: 1 – окружность, разграничивающая зоны 2 (пассивную) и 3 (активную); 4 – режущая кромка ножа ротора; 5 – режущая кромка ножа статора; 6 – внутренняя окружная кромка; r – радиус внутренней окружной кромки 6; r X – радиус окружности 1; R – радиус наружной окружной кромки 7; α p – угол наклона режущей кромки 4 ножа ротора к радиусу r ; α c – угол наклона режущей кромки 5 ножа статора к радиусу r ; β – угол поворота режущей кромки 4 ножа ротора

• -    исходном, 4 ( AB^p ), когда она пересекается в точке A ещё и с осью ординат y ;

• -    промежуточном, 4 ( A ′ B^{Р ′} ), после поворота на угол β.

В результате поворота точка A переместилась по:

• -    внутренней окружной кромке 6 в положение A' ;

• -    режущей кромке 5 – в промежуточное положение A , являющееся произвольной точкой ^X

скрещивания режущих кромок 4;

• -    режущей кромке 5 – в промежуточное положение A_X , являющееся произвольной точкой

скрещивания режущих кромок 4 ( A'B Р ) и 5 ( AB^C ), образующих между собой угол a СКР .

Одновременно точка B p переместилась по наружной окружной кромке в положение B p .

Линии:

• -    OA является радиусом r дуги AA' входной окружной кромки 6 сопряжённых кольцевых рабочих поверхностей дисков ротора и статора;

• -    OC_c , OC_p , перпендикулярные линиям AC_c , AC_P , продолжениям режущих кромок 5 ( AB^C ), 4 ( AB P ) , являются их эксцентриситетами, расположенными, как отмечалось выше, с противоположных сторон относительно центра O ;

• -    AO X является радиусом r X окружности 1 , образованной после поворота режущей кромки AB^p на угол β;

В источнике [1] алгоритмы радиуса r X для традиционного (двухстороннего) исполнения [2] рисунка кольцевых размалывающих ножевых поверхностей (с а A_KP = а _P +а C в точке A )

представлены в различных видах.

При α P > α C :

для ротора r _x = r ⋅

sin β⋅ cos( α c - ^β )

sin² α p + [ _β              ²     + cos α p ]²;

cos₂ ⋅ sin( α p +α c -β )

для статора r _x

=r⋅

sin² α + [ ^c

β sin β ⋅ cos( α _p - )

β cos2⋅sin(αp+αc-

- + cos ^а c ^] 2 . β )

При α P = α C = α:

для ротора и статора r _x

=r⋅

sin² α+ [

sin β⋅ cos( α - ^β ₂)

β cos 2 ⋅ sin(2α - β)

+ cos а ]² .

Необходимо отметить, что:

• -    алгоритмы (1), (2) и (3) являются неопределёнными, т. е. трансцендентными функциями, поскольку включают переменный параметр β – угол поворота режущей кромки 4 в направлении вращения диска ротора (см. изображённую на рисунке круговую стрелку);

• -    в алгоритмах (1) и (2) переменная величина α _P + α _C -β = α _С ^Х _КР ;                     (4)

• -    в алгоритме (3) переменная величина 2 ∙ α – = α _С ^Х _КР .                                (5)

Согласно существующим представлениям, для того чтобы волокнистый материал, находящийся между режущими кромками 4 (ротора) и 5 (статора), заклинивался между ними, – 701 – а не скользил по ним, α СXКР не должен превышать двойной угол трения материала φ об эти X кромки, т.е. а СКР < 2ф [2, 3]. Сделаем допущение, заключающееся в том, что произвольный угол скрещивания

X а скр = 2ф •                                                                 (6)

Также известно, что при движении точки скрещивания A x от внутренней окружной кромки 6 к периферийной кромке диска значения угла скрещивания α _С ^X _КР равномерно уменьшается [1, 4-6]. В этой связи становится очевидным, что окружность 1 разграничивает кольцевую размалывающую поверхность на две эоны:

• -    2 , ограниченную внутренней окружной кромкой 6 диска и окружностью 1 ;

• -    3 , ограниченную окружностью 1 и периферийной окружной кромкой диска.

Соответственно, режущая кромка 4 ( AB P ) ножа ротора также делится окружностью 1 на два отрезка:

• -    A'A x , расположенный в зоне 2 ;

• -    A X B P , расположенный в зоне 3.

Эти признаки вместе с допущением обусловливают то, что значения α _С ^X _КР в точках:

• -    зоны 2 превышают двойной угол трения материала о кромки, т. е. а СКР ) 2 ф (за счёт этого волокнистый материал, нависший на режущих кромках, не заклинивается между ними, а скользит по ним от центра О диска к его периферии);

• -    окружности 1 с произвольным радиусом r x равны двойному углу трения материала о кромки, т. е. а СКР = 2 ф (за счёт этого волокнистый материал, нависший на режущих кромках, заклинивается между ними);

• -    зоны 3 меньше двойного угла трения материала о кромки, т.е. а СКР ) 2 ф (за счёт чего волокнистый материал, нависший на режущих кромках, ещё сильнее заклинивается между ними).

С учётом данных особенностей назовём зону 2 пассивной , а зону 3, включая окружность 1, активной .

Результаты корректирования известного алгоритма

Под корректированием понимается устранение трансцендентности известного алгоритма. Это можно осуществить, выразив входящий в него переменный параметр в через входные (постоянные) величины.

Например, через изначально заданный произвольный угол скрещивания а _СКР . Точнее, согласно принятому выше допущению, через 2φ.

Тогда переменные параметры, включающие угол поворота β и входящие в зависимости (1), (2), можно представить в виде нетрансцендентных (определённых) алгоритмов:

β = α _p + α _c - 2 ϕ согласно зависимостей (4) и (6);                                      (7)

β

α +α pc

-

2ф               ™ согласно зависимости (7);

α

β

p

^a p ^а + ^2ф 2

согласно зависимости (7);

α _c

β

αc - αp + 2ϕ 2

согласно зависимости (7).

Заменив левые части (7)(10), входящие в (1) и (3) на правые, получим также нетрансцендентные (определённые) алгоритмы:

Для ротора r _x = r ⋅

sin² α _p + [

sin( α _p + α _c

-

2 ϕ ) ⋅ cos(

α _c

-

αp +2ϕ

)

α

Для статора r_x = r ⋅

sin² α _c + [

cos

p

+α _c

-

2ϕ

+ cos α _p ]² .

⋅ sin 2 ϕ

sin(α p + α

c

-

2 ϕ ) ⋅ cos(

α

p

-

αc +2ϕ

)

α

cos

p

+α

c

-

2ϕ

+ cos α _c ]² .

⋅ sin 2ϕ

Переменные параметры, включающие угол поворота β и входящие в зависимость (3), можно тоже представить в виде нетрансцендентных (определённых) алгоритмов:

β = 2 ⋅ ( α -ϕ ) согласно зависимостей (5) и (6);                                         (13)

^β = α-ϕ согласно зависимости (13);

α- ^β = ϕ согласно зависимости (13);

2 ⋅α-β = 2 ⋅ϕ согласно зависимости (13).                                           (16)

Заменив левые части данных равенств, входящих в зависимость (3), на правые, получим также нетрансцендентный (определённый) алгоритм sin2⋅(α-ϕ)⋅cosϕ rx = r ⋅ sin2 α + [

+ cos α ]² .

cos( α - ϕ ) ⋅ sin2 ϕ

Обсуждение результатов

Нетрансцендентность полученных после корректирования алгоритмов (11), (12) и (17) объясняется тем, что они включают только входные, постоянные по величине, геометрические параметры.

Результаты анализа и корректирования известных алгоритмов (1), (2) и (3):

• -    дополняют накопленные знания по исследуемому вопросу;

• -    создают хорошие предпосылки для вывода аналитических зависимостей, характеризующих полезную часть длины режущих кромок ножей.

Заключение

Можно предположить, что для дальнейших исследований потребуется создание дополнительной математической базы и условий, направленных, в частности, на решение следующих задач:

• -    проведение корреляции основных технологических параметров с учётом величины полезной части длины режущих кромок ножей;

• -    выявление закономерностей влияния полезной части длины прямолинейных режущих кромок ножей на основные бумагообразующие свойства целлюлозы, физико-механические показатели отливок, а также на технологические и энергосиловые характеристики работы ножевых размалывающих машин;

• -    выявление наиболее оптимальных значений полезной части длины прямолинейных режущих кромок ножей для различных древесноволокнистых полуфабрикатов с учётом их физико-механических характеристик и свойств.