Алгоритм расчета арочной конструкции из составных упругопластических элементов

В работе излагается порядок расчета составной двухшарнирной упругопластической пологой арки, ось которой имеет круговое очертание. Арка имеет переменное сечение по длине. Пояса арки соединены между собой структурными связями (раскосами, распорками, планками, перфорированным листом). В работе используется приближенное выражение для кривизны изогнутой оси. Для материала арки устанавливается произвольная зависимо сть между деформациями и напряжением. Учет влияния деформаций сдвига осуществляется способом, предложенным Ф. Энгессером и С. П. Тимошенко [6; 133]. Не учитывается влияние касательных напряжений на развитие пластических деформаций. Геометрическая неизменяемость поперечного сечения со ставной арки обеспечивается постановкой поперечных диафрагм же стко сти.

В основе предлагаемого решения лежит использование известного дифференциального уравнения изгиба упругой пологой арки, имеющей бесконечную жесткость на сдвиг, d2 f^r/\d2v(x))        d2v(x)   1 )   / A n

—IEJ(x) —— 1+N(x)Hy^+^l-q(x)=0, (1) dx2 V       dx2 J V dx2    Ro J где EJ(x) – изгибная жесткость поперечного сечения арки, изменяющаяся по ее длине; v(x) – перемещение точек оси арки в радиальном направлении; N(x) – продольная сила, действующая в сечениях арки; Ro – радиус кривизны оси недеформированной арки; q(x) – неравномерно распределенная нагрузка, действующая на арку в ее плоскости в радиальном направлении.

Для решения уравнения (1) используется метод конечных разностей и шаговое нагружение конструкции [1]. Проекция оси арки на ось ординат x делится на m равных частей длиной s . Для j -й узловой точки на оси арки уравнение (1)

на i -м шаге нагружения примет вид уравнения в конечных разностях

„ экв ( i ) ^А 4 v j i

B xj      s 4

+ N j )

(Aj. +  )

I s ²     R o J

— q j ) = 0,

где A ² v⁽ j ) и A ⁴ v j ) - конечные разности соответственно второго и четвертого порядков на i -м шаге нагружения; q j ) - равномерно распределенная нагрузка на j -м участке арки во время i -го шага нагружения; B j ^{( 1}) - эквивалентная жесткость поперечного сечения арки, учитывающая влияние сдвиговых деформаций, равная для i -го шага нагружения

где N j ^{- 1)} - продольная сила, действующая в j -м поперечном сечении арки, возникающая при ( i - 1 ) -м нагружении.

Для упрощения решения системы нелинейных алгебраических уравнений (6) j -е поперечное сечение арки разбивается по высоте на n участков одинаковой ширины. Принимая во внимание отно сительные деформации на границах k -го участка разбиения j ) и f j - ¹) , вместо (6) в расчете используется система уравнений

B экв ( i ) =

M Xj ^{- 1)}

( A f j ^{- 1)} / h j - / ( j» Q ^i ^-T

V Mii-D(Ai-D A i -1)4  Л^С-Ч - 0

A M jk (fjk 1 , fjk 2 ) - M j   = 0, k=0

V pHM i -1) A i -1)4  V ^l: - 0

A Pjk  (fjk 1, fjk2) - Nj = 0, k=0

Формула (3) была получена и опубликована нами ранее [4]. В этой формуле: M x ^-1)- изгибающий момент в j -м сечении арки, возникающий при ( i - 1 ) -м шаге нагружения; Af ( ^{- 1)} - разность краевых линейных относительных деформаций в j -м сечении арки при ( i - 1 ) -м шаге нагружения; h j - высота j -го поперечного сечения арки; у !‘j ) - угол сдвига соединительной решетки составной арки от единичной поперечной силы для j -го участка арки при ( i - 1 ) -м шаге нагружения; Q j ^{- 1)} - значение первой производной от поперечной силы, действующей в j -м сечении арки при ( i - 1 ) -м шаге нагружения.

При известной функциональной зависимости между напряжениями и деформациями с т = f ( f ) для материала стержневого элемента краевые продольные относительные деформации в j -м сечении элемента при ( i - 1 ) -м нагружении являются функциями усилий

где M j ^ и p ki ¹¹ - коэффициенты, зависящие от формы, размеров поперечного сечения арки, от интервала разбиения и стадии напряженно-деформированного состояния в j -м сечении при ( i - 1 ) -м нагружении арки;

( i - 1) _ „( i - 1Ы i - 1) , /,( i - 1) z.( i - 1) . ^f jk 1 = a jk 1 ^f j 1    ⁺ b jk 1 ^f j 2   ;

( i - 1) _ „( i - 1Ы i - 1) , /,( i - 1)z.( i - 1) . ^f jk 2 = a jk 2 ^f j 1    ⁺ b jk 2 ^f j 2   ;

здесь a ⁽ _j ⁱ _k ^- ₁ ¹⁾ , a ⁽ _j ⁱ _k ^- ₂ ¹⁾ , b ⁽ _j ⁱ _k ^- ₁ ¹⁾ , b ⁽ _j ⁱ _k ^- ₂ ¹⁾ - коэффициенты, учитывающие линейное распределение деформаций по высоте поперечного сечения.

При известных величинах Mx^-1) и Pji ¹¹ с помощью формул (4)-(9) в j -м поперечном сечении .находятся относительные деформации f ⁽ j ^{- 1}) и f 2 ij 1) и по (3) определяется величина B³ j ⁽ i ) .

Формула (2) в неизвестных перемещениях узловых точек примет вид

с(i-1) _ Ai-1)/Д4™(i-1) Рв«(i-1)Дz,x f1 j   = f1 j  (Mxj    , Pj     ),(4)

r(i-1) _ Ai-1)f4,/вн(i-1) рвн(i-1h f2j   = f2j  (Mxj    ,Pj     ),(5)

R ( i ) Xfj i ) ^Вэкв , j s 4 ( Р / - 2

- 4j1 + 6Vj) - 4Vj+1 + Vi+2)+

где M xj ⁽ i ^{- 1)} - главный момент эпюры нормальных напряжений относительно центра тяжести j -го поперечного сечения, возникающий при ( i - 1 ) -м нагружении арки; P j^{H (} i ^{- 1)} - главный вектор эпюры нормальных напряжений в этом сечении при ( i - 1 ) -м нагружении арки.

Краевые деформации fj ’'' и fj ’ определяются из решения системы уравнений равновесия

+ Nfl (zj-, - 2z"' + Vy

-

(10) q j ) = 0.

Продольная сила в j -м сечении арки, используемая при расчете на i -м шаге нагружения, определяется по формуле, полученной в работе [2],

Л/Гвн ( i - 1)/Д i - 1) f( i - 1)^ — Л/f( i - 1)

^Mxj    ^{( f} 1 j  , ^f 1 j  ) = ^Mxj ,

P j ^{H (} i ^{- 1)} ( f j 1) , f j 1) ) _ N ji ^{- 1)} ,

—        B ⁽ i ^{- 1)}

N ^{( i )} = N C⁽i ^1:-- экв : 1

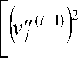
R 0

где NC^ i - ) - продольная сила, возникающая в точке перегиба после ( i - 1 ) -го шага нагружения;

(i-1) - Л2,,( i -1) / с.2 _ L( i -1)          i 1 , _v( i -1) V с.2

v j    ^-Л v j / ^{s -} \ v j - 1 ^{- 2 v} j + ^v j + 1 ) / ^s •

Ордината j -го узла деформированной оси арки у(-1) в системе координат у - x определится по формуле yj-1) - yRo,j - Vj-1),                 (12)

где у Ro , j - ордината j -го узла недеформирован-ной оси арки.

Зная у j ^{- 1)} , построим алгебраический интерполяционный многочлен Лагранжа m -го порядка

m

L m ^{- 1)} ( x ) - £ l j (x ) у j ^{- 1)} ,             (13)

j - 0

где l j ( x ) - коэффициенты полинома Лагранжа [3].

Абсцисса x C ^{- 1)} точки перегиба С деформированной оси арки определяется из решения уравнения

[ L m ^{- 1)} ( x ) ]" - 0.                    ⁽¹⁴⁾

Зная напряженно-деформированное состояние арки при ( 1 - 1 ) нагружении и x C ^{- 1)} , величина N_C^{(1 - 1)} определяется из решения системы уравнений равновесия части арки, отделенной поперечным сечением, проходящим через точку оси арки С .

С учетом вышеизложенного, принимая во внимание формулы (2)-(14), решается задача деформационного расчета нелинейной составной пологой арки переменного сечения.

В процессе описанного расчета на каждом 1 -м этапе нагружения проверяется устойчивость арки в своей плоскости методом, изложенным в [5]. Для рассматриваемой арки составляется и варьируется система уравнений равновесия в сечениях арки

1 + ( у j )² ] 3' : [ ^ + (V o - G ) у ] у j w j -

-1 + (уj)2] • \h + (Vo - GJW‘} + 5P™ - 0; (15)

Hдyj + 5Hyj + SM™ - 0,

где H - распор; V o - вертикальная реакция на левой опоре арки; G J - главный вектор внешней нагрузки, приложенной к левой части арки, отделенной j -м сечением;

5M™	_ д M™ 5 ^ 1 j	- д£ \ j +	д M вн W£ 2 j , О£ 2 j	(16)
5Ff	_ д P Jн д£ 1 j	§£ 1 j +	д Р вн £ . О £ 2 j	(17)

В определитель системы (15), составленный из коэффициентов при вариациях независимых переменных, подставляются параметры напряженно-деформированного состояния, полученные из деформационного расчета арки. В случае равенства нулю указанного определителя или смены знака его численного значения регистрируется величина критической нагрузки. Если устойчивость арки обеспечена, производится перерасчет величины B x™ ^{( 1} ) для следующего этапа нагружения арки и повторяется вновь ее деформационный расчет.