Алгоритм расчета допускаемых режимов работы энергетических и технико-экономических показателей МТА и его реализация в среде MAPLE

Введение. Эксплуатационные свойства машин, которые используются в сельском хозяйстве, оказывают решающее влияние на качество выполняемых технологических операций и на эффективность использования. От эффективности использования как отдельных агрегатов, так и всего машинно-тракторного парка непосредственно зависит количество и качество производимой сельскохозяйственной продукции, затраты соответствующих ресурсов и, в конечном итоге, экономическое благополучие всего хозяйства [1,2, 3].

Методы исследования. Для оценки работы машинно-тракторных агрегатов необходимы обоснованные допуски на уровень и точность настройки регулирующих устройств, а также на степень неравномерности изменения процессов (или параметров агрегата). На основе этих допусков могут быть определены допустимые значения статистических характеристик эксплуатационных показателей агрегатов: степень неравномерности 5_Х, коэффициент вариации v_X! дисперсия D_x или среднеквадратическое отклонение ст_х и др. Рассмотрим пример расчета дисперсии эффективной мощности [4, 5, 6]:

d^) = Л(У- WWjjfM - Й WW     (1)

где У- математическое ожидание выходного показателя СХА;

<р(У) = ф(X')\dX/dУ- плотность распределения вероятностей случайной величины y_t;

ф(Х) - плотность распределения вероятностей входной переменной;

f(X) - детерминированная функция, устанавливаемая в процессе стендовых и тяговых испытаний МТА.

Дисперсия эффективной мощности ДПМ с учетом выражений (1) рассчитывается по формуле [4, 5, 8,10]:

D(n_№) = (^VS)"¹

гМн

(А1 + В^Мк

- Мд_пмУ х

х exp [-(Mk - M^/^a^AdMk + гМп

+   (Л^ + B₂M_k - МдпмУехр V-(M_k - M_ky/(2a№Mk +

*J”_n(A*₃ + B₃M_k - N_finMyexp HM_k - М_кУ j^^^ = " ҚиДО-З + Ф(С_Н)] — 2K_1N B[ <у_мф(і_н") +

Ч-В^О^ + Ф(ін) + ^ф^ + К^^Ф^п) - 0(tj] + +2K2NB2cjMVp(tH) -

Реализуем данный алгоритм в MAPLE [7, 9].

Программа расчета дисперсии эффективной мощности > restart:

Угловые коэффициенты

• >    М — 549.26;

н

4^1=549.26

• >    М — 668.41;

4^—668.41

• > М — 732.35; шак

^=732.35

• >    Ы — 115.3; еН

• >    Н — 115.3;

еП

^:= 115.3

> N — 101.2; ешах

N : emas

101.2

> kl

М max

М

п

kl ~ 1.095659849

> k2

М п м '

н

£2 = 1 2169282 31

> А1 — 0 ;

А1 =0

> А2 — М + еН

еН еП

(к2-1) 7

А2 = 115.3

> АЗ ^ N + еП

f Н — М А еП етах .

"Тк^іГ

АЗ = 262 6972638

(б)

(Ю)

В1 =0.2099187998

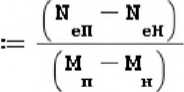
В2 = 0.

f Н — N 'I . етак еП ■

' Гм — м ' так п ВЗ = -0.2205192368

• >    а := (А1 + АЗ ); и '

й₀ = 262.6972638

• >    а := (Al — А2 );

a_v = -115.3

• >    а^ “ (А2 — АЗ);

у₂ = -147.3972638

>    Ь — (В1 + ВЗ ) ; о '              '

Ао := -0.0106004370

>    Ь1 — (В1 — В2);

6, = 0.2099187998

>    Ь2= (В2—ВЗ);

s2 = 0.2205192368

tH :- (549.26-Mk j tP — (668.41-Mk j

) / (sigma);

) /(sigma);

549.26 -ML tH- ----------4.

a

668.41 -Mk.

tP---------- a

> phil := evalf (exp ( - tH Л 2 / 2 ) * 1 / sqrt (2 * Pi ));

Phil = evalf (int( exp ( - tA2/2)*l / sqrt (2 *Pi) ( t = 0

--tH));

фі = 0.3989422802 e"⁰-⁵⁰®®¹⁰®⁰ ®²

Ф/ = 0.5000000000 erf(0.7071067810 tH^

> рһі2 := evalf ( ехр( -tP A2/2) *1 / sqrt( 2 *PiI) ;

Phi2 — evalf(int(exp( -tA2/2) *1/ sqrt(2 *Pi ), t = 0 ..tP));

0.5000000000 ,668.41 - l.№ 1

ф2 ” 0.3989422802 e

Ф2 := -0.5000000000 erf

' 0 7071067810 ( -668.41 4-^)

• >    sigma :— Vm| i *Mk[j];

  
  

о := Vm_t Mk.

• >    N — evalf 0.5 - । a I b -Mk I j 1 ^лі + i b -Mk I j + a , -Phil V , 0        0            )     ( 1                  1

0.7071067810 (-549.26 4-^.) 7m, Mk,

+ i b Mkf 3 + a I -Phi2 — sigma- । b -phil + b -phi2 , 2                2                         ( 1              2

N” 131.3486319 - 0.00530021850^- 0.5000000000 (0.2099187998 Mk_j

- 115.3) erf

- 0.5000000000 (0.2205192368 Mk^

- 147.3972638) erf

' 0.7071067810 (-668.41 4- Mk^ 7m, Mk,

Функции (для упрощения выражения)

> KI := Al I Bl *Mk[j K2 := A2 I B2 *Mk j КЗ :™ АЗ I B3 *Mk j

- N :

— N :

N :

_ Дисперсия эффективной мощности ДИМ

• >    Dn — evalf (К1 ^л2 * (0.5 + Phil)-2 *K1 *B1 * sigma *phil

+ Bl л2 * sigma A 2 * (0.5 + Phil - tH * phil) + K2 A 2

* (РҺІ2-РҺІ1) + 2 *K2 *B2 * sigma * (phil-phi2) + B2 A 2

• *    sigma^A2 * (РҺІ2-РҺІ1 + tH *phil-tP *phi2 ) + КЗ ^A 2

• *    (0,5 -Phi2 ) + 2 * КЗ * B3 * sigma * phi2 + B3 ^A 2 * sigma ^A 2

• *    (0.5-РҺІ2 + tP *phi2 )) :

Задаем массив д.пя коэффициента вариации

• >    Vm := arrayll . .5 , [0.001, 0.133, 0.167, 0.25, 0.333]),

7m = I 0.001 0.133 0.167 0.25 0.333 ]                               (26)

Задаем массив для среднего значения момента

• >    Mk “ array(l . .6, [401.046, 467.887, 546.16, 646.3, 668.41, 669.7]);

Мк~\ 401.046 467.887 546.16 646.3 668.41 669.7 ]                     (27)

Расчет дисперсии > for i from 1 to 5 do for j from 1 to 6 do;

(sigma,Mk[j],Vm[i],tH,phil,Phil,tP,phi2,Phi2,N[ (i-1)*6+j],Kl,K2,КЗ,Dn,

printf ("           Vm=%.3f,     Mk=%.3f, N=

%.3f,      D=%.3f\n",Vm[i] ,Mk [j],N,Dn))

end do;

end do;

7т=0.001,	Mk=401.046,	N=84.187,	D=0.007
Vm=0.001,	Mk=467.887,	N=98.218,	D=0.010
Vm=0.001,	Mk=546.160,	N=114.649,	0=0.013
Vm=0.001,	Mk=646.300,	N=115.300,	D=0.000
Vm=0.001,	Mk=668.410,	N=115.241,	D=0.007
Vm=0.001,	Mk=669.700,	N=115.014,	0=0.021
Vm=0.133,	Mk=401.046,	N=84.178,	0=124.743
Vm=0.133,	Mk=467.887,	N=97.631,	0=143.943
Vm=0.133,	Mk=546.160,	N=108.581,	0=82.858
Vm=0.133,	Mk=646.300,	N=108.758,	0=92.52 9
Vm=0.133,	Mk=668.410,	N=106.700,	0=130.067
Vm=0.133,	Mk=669.700,	N=106.560,	0=132.586

Проверкой расчетов может послужить тот факт, что при коэффициенте вариации, равном нулю, дисперсия тоже равна нулю, что мы и наблюдаем.

В (1), (2) и (3) строках задаются номинальный, предельный и максимальный момент на валу двигателя.

В (4), (5) и (6) строках - значения эффективной мощности, соответствующие номинальному, предельному и максимальному значениям крутящего момента на валу двигателя.

В строках (7) и (8) - коэффициенты.

В строках с (9) по (20) рассчитываются постоянные величины и угловые коэффициенты эффективной мощности двигателя.

В строке (21) рассчитываются аргументы функции Лапласа.

В строках (22) и (23) определяются табулированные плотности вероятности и интегральные функции Лапласа.

В строке (24) рассчитывается среднеквадратическое отклонение.

В строке (25) рассчитывается эффективная мощность двигателя.

В строках (26) и (27) задается массив для коэффициента вариации и крутящего момента.

Для расчета дисперсии и вывода результатов вычислений используется вложенный цикл.

Графическая интерпретация расчетов представлена на рисунке.

> р/ол [ DhI. Dn2. Dtt3. Du-#!, Mk [ j ] = О „650, labels = [MD], thickness =6, labelfont = [ TIMES, BOLD, 18 ])

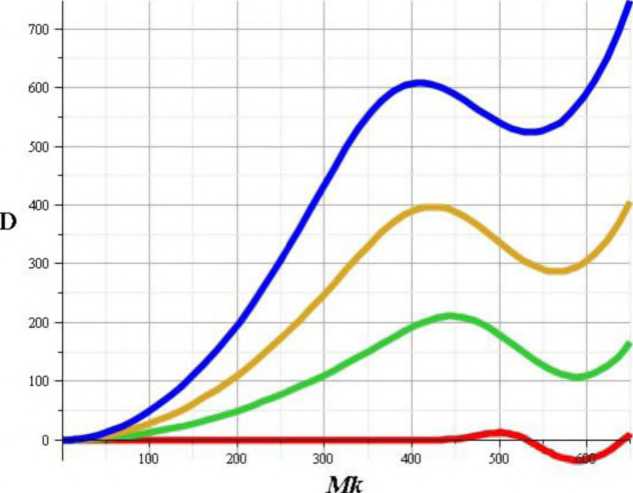
Закономерности изменения дисперсии эффективной мощности в зависимости от крутящего момента двигателя и коэффициента её вариации (1 - Ум = 0; 2 - Vm = 8,3%; 3 - v_M = 16,7%; 4 - v„ = 25,0%)

Выводы. Расчет дисперсии, реализованный в Maple, позволяет прогнозировать и определять значения эксплуатационных допусков на диагностируемые в процессе технического обслуживания энергетические параметры тракторов.