Алгоритм расчета химического равновесия на основе минимизации энергии Гиббса

Компьютерное моделирование химических процессов позволяет эффективно проектировать новые технологические процессы; экономить время и ресурсы при проведении экспериментов; проводить исследования, которые невозможно осуществить экспериментальным путем из-за высокой стоимости, экологических рисков и др.; исключить влияние посторонних факторов на исследуемый объект. Существенной частью моделирования химических процессов является расчет термодинамически равновесного состояния химической системы.

В литературе представлены два основных подхода к нахождению равновесного состояния химической системы, основанных на решении системы стехиометрических уравнений и на нахождении экстремума термодинамического потенциала системы, соответствующего равновесному состоянию [4; Т. 2; 500–501]. Последний метод приобретает большую популярность в связи с возможностью эффективной реализации на ЭВМ. На практике традиционно рассматриваются изобарно-изотермические условия, в которых равновесное состояние системы характеризуется минимумом энергии Гиббса. Таким образом, задача расчета равновесного состояния системы основана на поиске химического состава системы, обладающего минимальной энергией Гиббса.

В литературе представлено достаточно большое число алгоритмов поиска химического состава системы с минимальной энергией Гиббса, часть которых основана на методе наискорейшего спуска (в частности, алгоритм, предложенный Уайтом, Джонсоном и Данцигом в 1958 году [8]), часть – на методе Ньютона [7] и его модификациях [2]. Подробный обзор данных алгоритмов представлен в работе [6]. Другие подходы, например использование метода внутренних точек [5], [6], получили меньшее распространение.

Энергию Гиббса системы (в случае использования уравнения идеального газа в качестве уравнения состояния) можно найти следующим образом [4; Т. 1; 132–133]:

G Ц x- g i k e P i e N_k

V

+ RT In x i

X x , j ^e N k   J

где N – индексное множество всех зависимых компонентов, N_k – множество зависимых компо-

нентов, принадлежащих фазе k , x_i – количество зависимого компонента i (в молях), P – индексное множество фаз, g_i – молярный потенциал Гиббса зависимого компонента i , вычисляемый по формуле:

_ р gi = Hi- ST + RT ln -,           (2)

P 0

где H_i – молярная энтальпия образования зависимого компонента i при температуре T , S_i – молярная энтропия образования зависимого компонента i при температуре T , R – универсальная газовая постоянная, P – давление системы, P₀ – давление, использовавшееся при определении S (в стандартных условиях, P₀ = 10⁵ Па).

Обозначим общее количество вещества в фазе k как yk, yk = У xt и разделим gi на RT. Тогда ieNk задача минимизации энергии Гиббса формулируется следующим образом:

F (x ) = УУ Xi I c + ln — | ^ min,(3)

к e Pi e N_k ^

при условии

У aijxi = bj, Vi e M,(4)

i e N xi > 0, Vi e N,(5)

Ук = У x,(6)

ieNk где M – индексное множество независимых компонентов, aij – стехиометрические коэффициенты (количество частиц независимого компонента j, входящих в состав одной частицы компонента i), bj – общее количество независимого компонента j в системе (в молях), коэффициенты целевой функции определяются по формуле c = gT = H i RT

- ST

RT

+ ln -

.

P 0

Укажем особенности задачи минимизации энергии Гиббса. Функция F является выпуклой в области определения, не определена при x_i = 0. Задача характеризуется относительно высокой размерностью (число переменных, соответствующих зависимым компонентам, может достигать тысяч, на практике часто встречаются задачи с более чем сотней переменных), при этом малым изменениям значений функции F могут соответствовать большие изменения переменных. Применение традиционных подходов, основанных на методе наискорейшего спуска и методе Ньютона, осложняется возможным вырождением системы линейных уравнений, решаемых на каждой итерации алгоритма, что может приводить к потере точности. В случае необходимости изменения состава фаз текущего решения происходят значительные изменения множителей Лагранжа, что также существенно затрудняет вычисления.

Для решения этой задачи будем использовать следующий вариант метода возможных направлений [3]. Для нахождения точек локальных минимумов общей задачи нелинейного программирования применяются релаксационные методы, в которых при вычислении направления спуска из некоторой точки x учитываются локальные свойства минимизируемой функции и локальные свойства множества X в окрестности точки x . Направление спуска в этом методе находят следующим образом: строят в точке x конус возможных направлений, который задается системой линейных равенств, и выбирают в этом конусе вектор конечной длины, составляющий острый угол с антиградиентом целевой функции.

Суть метода такова. Рассмотрим задачу минимизации выпуклого дифференцируемого функционала F в выпуклой ограниченной области X пространства Rⁿ :

F ( x ) ^ min, x e X. (8)

Выберем произвольную точку x⁰ ∈ X.

Для поиска направления спуска s^t в текущей точке x^t ∈ X решается задача

a* ^ max,

У dF (xt)st + ^t < 0,(10)

i dxi

[xt, xt + st ] cX.(11)

Если σt ≤ 0, то x – точка локального минимума. Иначе переходим к следующей точке xt+1 = min F (x) xe[ xt, xt + st ]

В применении к задаче минимизации энергии Гиббса метод возможных направлений имеет следующие особенности. Усилим ограничение (5):

x i >  0, V i e N . (13)

Производная имеет вид:

dF          x

—^{( x} ) = c , + ln   .            (14)

dxi             yk

Целевая функция и множество допустимых значений выпуклы, следовательно, локальный минимум является глобальным.

Применим ограничение (11) к рассматриваемой задаче:

	A ( xt + st ) = B ,	(15)
	x t + s t >  0 V i e N It   ,      ,	(16)
получаем
	Ast = 0,	(17)
	- s , - <  x, .	(18)

Таким образом, возможное направление из точки xt на каждом шаге для задачи с нелиней- ной целевой функцией и линейными ограничениями определяется следующим образом:

ст* ^ max,(19)

УdF (xt)st + ^ < 0,(20)

i dxi

Ast = 0,(21)

- si < xt.(22)

Задача (19)–(22) представляет собой задачу линейного программирования (ЛП). Метод возможных направлений требует решения задачи (19)–(22) на каждом шаге, что является затратным при большом количестве итераций алгоритма. Используем возможность заменить решение задачи ЛП модификацией предшествующего ре- шения.

Шаг 1. На каждой итерации получаем текущее решение xt и множество Bt ⊂ N, образующее базис по столбцам ограничений Ai, i ∈ Bt. Возможные направления будем находить следующим образом: для каждой небазисной переменной с индексом q ∈ N \ Bt можно построить вектор zq,   i e S', s = 1- 1, i = q,

0,   иначе, где ziq – разложение Aq по базису Bt.

Для заданного s выполняется уравнение (21).

Действительно,

У As = У As - As = У Az - У Az = 0 ii       ii qq       ii      ii .

i e N            i e S '                         i e S '             i e S '

Найдем значение У dF (x')s‘. Если значе-i dxi ние отрицательно, то s удовлетворяет условиям (21)–(22), если значение положительно, то s удовлетворяет условиям (21)–(22). Иначе данное направление не подходит для поиска решения.

Среди всех возможных направлений находим направление с минимальным значением У dF ( x ' ) s t <  0 .

i dx_i

Решение найдено, если невозможно найти новое направление.

Шаг 2 . Найдем d = max{ l : x_i + ls_i ≥ 0, ∀ i ∈ N }.

Рассмотрим переход к следующей точке, найдем d * = argmin F (x' + hs).          (24)

h e [0, d ]

Функция F(x) выпукла, что позволяет находить d^* методом дихотомии. Действительно, x^t+1 = x^t + d^*s . Построим новый базис:

• •    если 3 i e S ' : x ' + d * s i = 0 , то S ' ^{+ 1} = S ' и { q } \ { i } ,

• •    иначе, если j B^t :| F_x ( x^{t 1} ) | | F_x ( x^{t 1} ) | , то,

S‘ ^{+ 1} = S‘ и { q }\{ i } j q

• •    иначе B^{t +1} = B^t .

После построения нового базиса – переход к шагу 1.

Начальные решение и базис задаются с помощью дополнительных переменных с единичной матрицей и c_i = + ∞ .

При реализации алгоритма в виде программной системы использовалась универсальная библиотека UPS Framework, созданная специалистами IT-парка ПетрГУ на основе многолетнего опыта разработки и внедрения программных систем [1]. Библиотека включает большое количество тесно интегрированных друг с другом программных компонент, позволяющих унифицировать процессы и ускорить разработку модулей системы, упростить программное описание моделей данных, уменьшить количество ошибок. В частности, в нее входит модуль UPS.Solver для решения сложных оптимизационных задач планирования производства («универсальный решатель»). Все компоненты UPS Framework интегрированы в среду программирования MS Visual Studio .NET, что позволяет свободно и единообразно использовать их вместе со стандартными методами и компонентами MS Visual Studio.

Матрица ограничений в данной задаче оптимизации имеет достаточно большую размерность и ярко выраженную специфическую блочную структуру. С учетом большого количества блоков матрицы ограничений определение и задание их взаимного расположения часто приводит к трудноустранимых ошибкам. Поэтому в составе UPS. Solver реализована специальная структура данных для повышения эффективности хранения и использования данных с учетом структуры подматриц – «матричный конструктор».

Линеаризация выпуклого аддитивного функционала задачи (3)–(6) приводит к необходимости последовательного построения большого количества столбцов [8]. С целью учета особенностей используемого способа применения градиентного метода был использован модуль UPS. Solver, базовым методом которого является метод генерации столбцов. Его основное отличие от других методов в том, что проверка оптимальности решения осуществляется не с использованием матрицы исходных данных, а путем решения вспомогательной задачи оптимизации.

Представленный алгоритм был проверен на наборе тестовых данных собственной разработки. В качестве альтернативного подхода использовался алгоритм Уайта [7], который обычно используется в коммерческих программных продуктах для решения данной задачи. Термодинамические данные для тестов брались из базы данных, входящей в пакет HSC Chemistry 6.1 (разработка Outotec Oyj, Финляндия).

Использованный набор тестовых данных состоит из 30 химических систем, для каждой из которых было создано от 20 до 100 отдельных задач минимизации энергии Гиббса при различных исходных количествах веществ, температурах и давлениях. Набор тестовых данных условно состоит из двух частей: набора относительно простых и относительно сложных химических систем. Простые системы характеризуются следующими свойствами:

• •    малым количеством зависимых компонентов (< 50),

• •    невырожденной матрицей ограничений,

• •    обусловленностью целевой функции в окрестности оптимального решения.

Для простых химических систем равновесное состояние успешно находится алгоритмом Уайта. В случае сложных химических систем алгоритм Уайта иногда находит оптимальное решение не во всех точках, что приводит к «зигзагам» и «дырам» при построении графиков количеств веществ для близких химических систем (рис. 1, 2).

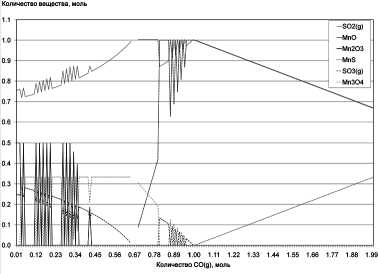
Рис. 1. График количеств веществ для сложной химической системы, найденных алгоритмом Уайта

Из представленных в таблице результатов тестирования видно, что предлагаемый алгоритм успешно находит равновесный состав для систем.

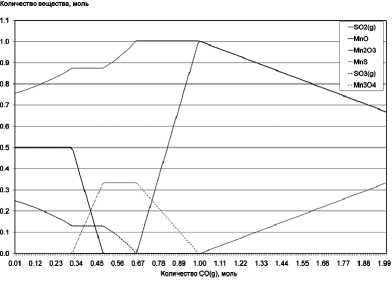
Рис. 2. График количеств веществ для сложной химической системы (рис. 1), найденных представленным в статье алгоритмом

Результаты тестирования предложенного алгоритма и алгоритма Уайта

		Алгоритм Уайта, решено тестов			Новый алгоритм, решено тестов
Тип тестов	Всего тестов	Полнос-тью	Час-тич-но	Не решено	Полнос-тью	Час-тич-но	Не решено
Простые	10	10	0	0	10	0	0
Сложные	20	1	13	6	20	0	0
Итого	30	11	13	6	30	0	0

ЗАКЛЮЧЕНИЕ

В работе представлен алгоритм нахождения термодинамически равновесного состава химической системы на основе минимизации энергии Гиббса, который был успешно применен к решению практических задач. Алгоритм может применяться и для более широкого круга задач минимизации выпуклого дифференцируемого функционала в выпуклой ограниченной области пространства Rⁿ . Примером является задача нахождения равновесного состава химической системы с функциональными коэффициентами активности.

* Работа выполняется при финансовой поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности.